【杂题总汇】UVa-1336 Fixing the Great Wall
【UVA-1336】Fixing the Great Wall
一开始把题看错了……直接用的整数存储答案;之后用double存最后输出答案的时候取整就AC了😂
⭐小紫薯例题 +vjudge链接-传送门+
◇ 题目
<手写翻译>
派遣一个机器人去修复一条直线上的n个点,机器人有一个速度v(单位/秒),且一开始在坐标x。对于第i个点,若立即修复它,需要花费ci,但是未修复的点会随着时间损坏,修复难度也增加,若第i个点未修复,则每过一秒将会增加Δi的额外花费。
<输入输出>
多组数据。每组数据第一行依次给出修复点的数量n,机器人的速度v以及它一开始的位置x。接下来n行,每行描述一个修复点,依次给出点的坐标,立即修复的花费以及每秒增加的额外花费(输入时点的坐标不一定有序)。
数据以n=0,v=0,x=0结束,不处理该数据。
对于每组数据,输出修复所有点的最小花费(存在浮点数,输出答案时忽略小数位取整)。
<样例&解释>
| 输入 | 输出 | 解释 |
|
3 1 1000 |
2084 1138 |
对于第一组数据,修复顺序为 1000->998->1010->996 从起始点1000到修复点998,到达时间为2,额外花费600,总花费600; 从998到1010,到达时间为14,额外花费为1400,总花费2000; 从1010到996,到达时间为28,额外花费为84,总花费为2084; |
◇ 解析
由于修复一个点不需要时间,所以最优方案一定不会跳过一个点到达另外一个点去修复,而是每到达一个点就修复,然后到达另一个点。因此机器人走过的点都会被修复——不难发现被修复的点是一个区间!
所以容易想到区间DP。和类似的题一样,状态定义为dp[l][r][k],表示修复了点l~r,且k=0/1在左/右端点时的最小花费。但是注意到每个点花费是随着时间增长的,再把时间储存在状态中显然是不现实的,但是解决方法也很简单——我们可以处理出从当前区间的某个端点u到达要修复的点v的时间内,没有修复的点的花费总共增加了多少,由于u到v的时间固定,我们只需要确定没有修复的点每秒总共增加多少花费,可以用前缀和解决。
举个例子:现在已经修复的区间是3~7,机器人在7修复点,下一步到达2修复点。那么没有修复的点的每秒增加的额外花费inc为 Δ[1~2]+Δ[8~n],计算出从7到2需要的时间tim,则这段时间内产生的额外花费为inc*tim。由于这些额外花费是不可避免的,我们将它一齐存入dp数组里。
那么dp[l][r][k]现在的含义是已经修复l~r,且现在(k=0/1)处于左/右端点时,已经支付的花费和未支付但必定存在的额外花费(也就是没有修复的点的花费已经随着时间增加了,而我们要修复所有点,这些新的额外花费也一定会算入最后的总花费,就可以将这些额外花费直接加入当前的花费,而保持其他点的花费不变)的和。则利用刷表法,可以得到状态转移方程式如下:
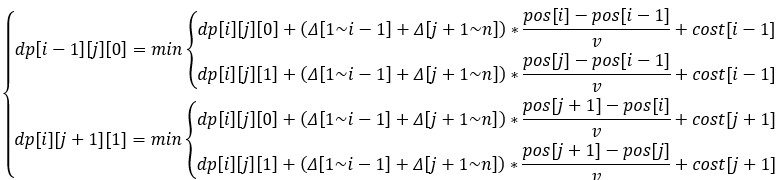
只是看起来复杂……🙃
Δ[l~r]可以用前缀和处理,式子中的(Δ[1~i-1]+Δ[j+1~n])表示的是除去已经修复的点i~j外,其他未修复的点每秒增加多少花费;(pos[i]-pos[i-1])等类似的式子计算的是从当前点到目标点的距离,除以速度v,得到需要的时间,与每秒增加花费相乘得到必定支付的额外花费;再加上修复目标点的花费cost。
其他就没有什么麻烦的了~
◇ 源代码
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=1000;
const double INF=1e17;
struct FIXPOINT{ //需要修复的点
double pos,del,cst; //位置,每秒增加花费,修复原花费
bool operator <(const FIXPOINT B)const{return pos<B.pos;}
}fix[MAXN+5];
int n,case_cnt; //点数量,当前数据组数
int vis[MAXN+5][MAXN+5][2]; //vis[i][j][k]:是否计算过dp[i][j][k]
double sum[MAXN+5],dp[MAXN+5][MAXN+5][2]; //前缀和,dp数组
double v,beg_pos; //速度,起始位置
double DP(int L,int R,int k){
if(L==1 && R==n) return 0; //终止位置,全部修完
if(vis[L][R][k]==case_cnt) return dp[L][R][k];
vis[L][R][k]=case_cnt;
double inc=sum[L-1]-sum[0]+sum[n]-sum[R],tim,pos=k? fix[R].pos:fix[L].pos;
//inc:每秒增加花费,tim:到达目标点花费时间,pos:当前位置
double &res=dp[L][R][k]=INF;
if(L-1>=1) //修复点L-1
{
tim=(pos-fix[L-1].pos)/v;
res=min(res,DP(L-1,R,0)+inc*tim+fix[L-1].cst);
}
if(R+1<=n) //修复点R+1
{
tim=(fix[R+1].pos-pos)/v;
res=min(res,DP(L,R+1,1)+inc*tim+fix[R+1].cst);
}
return res;
}
int main(){
//freopen("in.txt","r",stdin);
while(~scanf("%d%lf%lf",&n,&v,&beg_pos) && n)
{
case_cnt++;
for(int i=1;i<=n;i++)
scanf("%lf%lf%lf",&fix[i].pos,&fix[i].cst,&fix[i].del);
sort(fix+1,fix+n+1); //按位置排序
fix[0].pos=-INF;fix[n+1].pos=INF; //保证i(1<=i<=n)满足pos[i-1]<pos[i]<pos[i+1]
for(int i=1;i<=n;i++)
sum[i]=sum[i-1]+fix[i].del; //处理前缀和
double ans=INF;
for(int i=0;i<=n;i++)
if(fix[i].pos<beg_pos && beg_pos<fix[i+1].pos) //起始位置在i和i+1之间
{
double inc=sum[n],tim;
if(i>=1) //若先修点i
{
tim=(beg_pos-fix[i].pos)/v; //时间花费
ans=min(ans,DP(i,i,0)+tim*inc+fix[i].cst); //处理答案
}
if(i+1<=n) //先修点i+1,同上
{
tim=(fix[i+1].pos-beg_pos)/v;
ans=min(ans,DP(i+1,i+1,0)+tim*inc+fix[i+1].cst);
}
break;
}
printf("%lld\n",(long long)(ans));
}
return 0;
}
The End
Thanks for reading!
- Lucky_Glass


