【杂题总汇】UVa-1627 Team them up!
【UVa-1627】 Team them up!
借鉴了一下hahalidaxin的博客……了解了思路,但是莫名Wa了;最后再找了一篇dwtfukgv的博客才做出来🤨
⭐小紫薯例题
◇ 题目 +传送门(Vjudge)+
<手写翻译>
有n个人,将他们分为恰好两组。使得两组满足一下条件:
■ 同一组里的人互相认识;
■ 两组人数尽可能接近;
现给出n个人的认识关系(单向),求如何分组能够满足上述条件,若能够分组,输出最优分组,存在多解时输出任意一种;若无法分组,输出"No solution"。
<样例&解释>
输入 |
输出 |
解释 |
|
2 |
No solution (空行) 3 1 3 5 2 2 4 |
(1)无论如何都不能分为恰好两个组使得每组内的人互相认识; (2)互相认识的人有1/2,1/3,1/5,2/3,2/4,2/5,3/5, 此时将1,3,5分为一组,2,4分为一组,人数最接近 |
◇ 解析
直接考虑人互相认识的关系不太好考虑,但本题的两组可看为二分图的两个部,从而转换为图论考虑。
只要两个人不是互相认识,他们一定处于不同的组中,但是并不是说两个人互相认识就一定在一个组中(如样例,这也是为什么考虑互相认识的关系不方便)。换句话说,如果两个人不互相认识,他们就在不同的部中。于是我们以“不互相认识”关系建立一个图——只要两人不互相认识,就在他们之间连一条边;所以图中相邻(连边)的两人一定不同组。那么我们就可以利用二分图染色,判断是否能够分为两组,即相邻节点颜色不同。注意到新建立的图不一定全连通,需要依次对每一个连通块进行染色,只要有一个连通块染色失败,整个图都染色失败,输出"No solution"。
染色成功后,每一个连通块中,不同颜色的人必定分在不同组中,又因为只有两个组,相同颜色的人必定分在同一个组中。这样我们可以用vector的数组 blk[i][0/1] 记录第i个连通块中染成0的元素以及染成1的元素(注意计算前清空)。那么对于连通块i,记其分为两组的人数之差为val[i],则 val[i]=blk[i][0].size()-blk[i][1].size()。虽然我们把每一个连通块都分成了01两组,但是由于两个不同连通块互不影响,也就是说最终分组时,连通块i中染色为0的人不一定和连通块j中染色为0的人分为一组;每一个连通块中的分组仅仅对于该连通块有效。
那么现在问题就变成了从每一个连通块中选出一个组分为整体的第一组,剩下的组分为第二组,使得两组人数最接近。由于只有两组,且总人数确定,我们只要确定第一组的人数就可以求出第二组的人数。因此我们设dp[i][j]为前i个连通块分给第一组共j人的情况是否存在。那么状态转移就非常好想,因为第i个连通块要么把它的颜色为0的人分到第一组,要么把颜色为1的分到第一组,所以可以得到递推式如下:
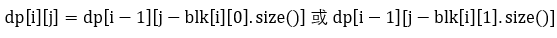
计算完成后,为了人数尽量接近,我们从n/2开始向两边查找,若找到第一个 dp[nblk(连通块的数量)][j]==true ,就说明最小相差 |n-2j| ,其中第一组有j人。
用一个Print()函数倒推计算分组——先将上面枚举出的j赋值给ans代入Print中,再定义ans1,ans2分别表示第一、二组有哪些人。倒序枚举i=nblk~1,此时的ans表示前i个连通块中分给第一组的人数,若dp[i-1][ans-blk[i][0].size()]==true,则说明第i个连通块把染色为0的分给第一组,则更新ans1和ans2,并将ans-=blk[i][0].size(),表示前i-1个连通块分给第一个组的个数;否则选择染色为1的组,作相同处理。
最后输出解,记得每两组数据之间要间隔一个空行。
(应该都看懂了吧😊)
◇ 源代码
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int MAXN=110;
int T,n; //数据组数,总人数
int col[MAXN]; //第i个人染成的颜色
bool knw[MAXN][MAXN]; //dp[i][j]==1 表示i认识j(单向)
bool dp[MAXN][MAXN]; //dp[i][j]表示前i个连通块分给第一组j人
vector<int> blk[MAXN][2];int nblk; //nblk是连通块的数量,blk[i][0/1]存储连通块i中染成0/1的人
bool DFS(int u,int clr){
col[u]=clr+1; //染色(实际上染成0颜色的标记为1,染成1颜色的标记为2)
blk[nblk][clr].push_back(u); //保存连通块信息
for(int v=1;v<=n;v++)
if(v!=u && !(knw[u][v] && knw[v][u]))
{
if(col[v] && col[u]==col[v]) return false; //若相邻两个节点颜色相同,则无法构成二分图,构造失败
if(!col[v] && !DFS(v,!clr)) return false; //只要有一个构造失败,则整体构造失败
}
return true;
}
bool Build_Graph(){
nblk=0;
memset(col,0,sizeof col); //清空
for(int i=1;i<=n;i++) //枚举每一个节点
if(!col[i]) //还未染色,即已经枚举到的连通块中并不包含元素i
{
nblk++; //新的连通块
blk[nblk][0].clear();
blk[nblk][1].clear(); //清空
if(!DFS(i,0)) return false; //整体构造失败
}
return true;
}
void Print(int ans){
vector<int> ans1,ans2; //第一组/第二组
for(int i=nblk;i>=1;i--)
{
int typ; //分给第一组的是染色为0的还是染色为1的
if(dp[i-1][ans-blk[i][0].size()]) typ=0,ans-=blk[i][0].size(); //染色为0的
else typ=1,ans-=blk[i][1].size(); //染色为1的
for(int j=0;j<blk[i][typ].size();j++)
ans1.push_back(blk[i][typ][j]); //存储答案
for(int j=0;j<blk[i][typ^1].size();j++)
ans2.push_back(blk[i][typ^1][j]); //另外的都是第二组的
}
printf("%d",ans1.size()); //输出
for(int i=0;i<ans1.size();i++)
printf(" %d",ans1[i]);
printf("\n");
printf("%d",ans2.size());
for(int i=0;i<ans2.size();i++)
printf(" %d",ans2[i]);
printf("\n");
}
void DP(){
memset(dp,0,sizeof dp);
dp[0][0]=true; //初始化
for(int i=1;i<=nblk;i++)
for(int j=0;j<=n;j++)
{
if(j-blk[i][0].size()>=0)
dp[i][j]|=dp[i-1][j-blk[i][0].size()]; //染色为0的
if(j-blk[i][1].size()>=0)
dp[i][j]|=dp[i-1][j-blk[i][1].size()]; //染色为1的
}
for(int i=n/2,j=(n+1)/2;i>0 && j<n;i--,j++) //从中间枚举,则第一个枚举到的就是两组之差最接近的
{
if(dp[nblk][i]) {Print(i);return;}
if(dp[nblk][j]) {Print(j);return;}
}
}
int main(){
//freopen("in.txt","r",stdin);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
memset(knw,0,sizeof knw); //清空认识关系
for(int u=1,v;u<=n;u++)
while(~scanf("%d",&v) && v)
knw[u][v]=true; //单向认识
if(!Build_Graph()) printf("No solution\n"); //构造失败
else DP();
if(T) printf("\n"); //每两组数据间隔空行
}
return 0;
}
The End
Thanks for reading!
- Lucky_Glass


