【学时总结】◆学时·VIII◆ 树形DP
◆学时·VIII◆ 树形DP
DP像猴子一样爬上了树……QwQ
◇ 算法概述
基于树的模型,由于树上没有环,满足DP的无后效性,可以充分发挥其强大统计以及计算答案的能力。
一般来说树形DP的状态定义有三种:偏简单的,dp[u]表示以u为根的子树的最优解/方案数;带选择性质的:dp[u][0/1],表示以u为根的子树中选择/不选择u的最优解/方案数;dp[u][i] 表示以u为根的子树中,u的状态为i的最优解/方案数(其实就是第二种定义的扩展)。
一般来说题目给的是一个树形图,那么我们只需要从图中一个存在的节点开始DP即可。注意向下DP时不要重复访问父节点。
由于树这种结构中,儿子与父亲的关系比较紧密,我们一般采用记忆化搜索,可以减免大量不合法的计算(只有儿子与父亲之间才能直接计算)。
◇ 经典选讲
(均出自《算法竞赛入门经典》-刘汝佳)
【UVa 12186】Another Crisis(工人的请愿书)
<题意>
某公司里有一个老板和n(n≤10 5 )个员工组成树状结构,除了老板之外每个员工都有唯一的直属上司。老板的编号为0,员工编号为1~n。工人们(即没有直接下属的员工)打算签署一项请愿书递给老板,但是不能跨级递,只能递给直属上司。当一个中级员工(不是工人的员工)的直属下属中不小于T%的人签字时,他也会签字并且递给他的直属上司。问:要让公司老板收到请愿书,至少需要多少个工人签字?
<解析>
这道题实质上是给定了一个以老板为根的有根树,于是我们DP的起点便是老板。定义状态为dp[u]为员工u签字最少需要多少个人签字。
对于工人u(没有直接下属),能够直接提供一个签字,即dp[u]=1,仅需要一人签字。对于其他非工人员工v,我们计算出他的每一个直属下属的dp值,存入cnt;再通过题目提供的百分数,算出要让他签字,他的直属下属员工最少有多少个需要签字,记为Maxi;那么要让v签字,最少要签字的人数为cnt中前Maxi个最小的值之和。
因为我们要使答案尽量小,取前Maxi个最小的值就可以达到目的。
(详见代码,如果有一些没懂的可以在邮箱里询问~)
<源代码>

1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 using namespace std; 7 const int MAXN=int(1e5); 8 vector<int> lnk[MAXN+5]; 9 int n,m; 10 int dp[MAXN+5]; 11 inline bool cmp(int A,int B){return dp[A]<dp[B];} 12 int DP(int u){ 13 if(dp[u]) return dp[u]; 14 if(lnk[u].size()==0) return dp[u]=1; 15 vector<int> cnt; 16 for(int i=0;i<(int)lnk[u].size();i++) 17 cnt.push_back(DP(lnk[u][i])); 18 sort(cnt.begin(),cnt.end()); 19 int Maxi=lnk[u].size()*m/100+(lnk[u].size()*m%100? 1:0); 20 for(int i=0;i<Maxi;i++) 21 dp[u]+=cnt[i]; 22 return dp[u]; 23 } 24 int main(){ 25 //freopen("in.txt","r",stdin); 26 while(~scanf("%d%d",&n,&m) && n && m) 27 { 28 memset(dp,0,sizeof dp); 29 memset(lnk,0,sizeof lnk); 30 for(int i=1,pre;i<=n;i++) 31 scanf("%d",&pre),lnk[pre].push_back(i); 32 printf("%d\n",DP(0)); 33 } 34 return 0; 35 }
【UVa 1220】Party at Hali-Bula(Hali-Bula的晚会)
<题意>
公司里有n(n≤200)个人形成一个树状结构,即除了老板之外每个员工都有唯一的直属上司。要求选尽量多的人,但不能同时选择一个人和他的直属上司。问:最多能选多少人,以及在人数最多的前提下方案是否唯一。输出第一个数为最多能选多少人,接下来若仅有一种选择方案能够达到最大选择人数,则输出Yes,否则输出No。
<解析>
本题相对上一题又多了一层状态——当前节点选或不选。也就是最开始在算法概述中描述的第二种状态定义。
先处理输入,我们先利用STL容器map<string,int>将名字映射到编号上,相当于重新编了号,固定“老板”的编号为1。
根据题意可知,对于一棵子树,若选取其根节点,则根节点的所有儿子都不能选;若不选根节点,则根节点的儿子可选可不选。那么我们DP开始时就要先判断“老板”这个节点选还是不选,即在dp[1][0]和dp[1][1]中取较大值。那么可以得到下面的状态转移方程式:
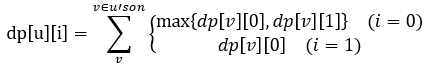
应该还是很好理解吧🙃……不懂的问邮箱……我再详细解答一下😶
下面就奉上代码啦~
<源代码>

1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<iostream> 6 #include<map> 7 #include<vector> 8 using namespace std; 9 const int MAXN=200; 10 int n; 11 map<string,int> nam;int cnt; 12 vector<int> lnk[MAXN+5]; 13 pair<int,bool> dp[MAXN+5][2]; 14 pair<int,bool> DP(int u,int f){ 15 if(dp[u][f].first) return dp[u][f]; 16 if(lnk[u].size()==0) {return dp[u][f]=make_pair(f,true);} 17 dp[u][f].second=true; 18 for(int i=0;i<lnk[u].size();i++) 19 { 20 int v=lnk[u][i]; 21 pair<int,int> res=f? DP(v,0):max(DP(v,0),DP(v,1)); 22 if(!f && dp[v][0]==dp[v][1]) res.second=false; 23 dp[u][f].first+=res.first; 24 dp[u][f].second=dp[u][f].second&&res.second; 25 } 26 dp[u][f].first+=f; 27 return dp[u][f]; 28 } 29 int main(){ 30 //freopen("in.txt","r",stdin); 31 while(~scanf("%d",&n) && n) 32 { 33 memset(dp,0,sizeof dp); 34 memset(lnk,0,sizeof lnk); 35 nam.clear();cnt=0; 36 string str;cin>>str; 37 nam[str]=++cnt; 38 for(int i=1,u,v;i<n;i++) 39 { 40 cin>>str;if(!nam.count(str)) nam[str]=++cnt;v=nam[str]; 41 cin>>str;if(!nam.count(str)) nam[str]=++cnt;u=nam[str]; 42 lnk[u].push_back(v); 43 } 44 pair<int,int> res=max(DP(1,0),DP(1,1)); 45 if(dp[1][0].first==dp[1][1].first) res.second=false; 46 printf("%d %s\n",res.first,res.second? "Yes":"No"); 47 } 48 return 0; 49 }
【UVa 1218】Perfect Service
<题意>
有n(n≤10000)台机器形成树状结构。要求在其中一些机器上安装服务器,使得每台不是服务器的计算机恰好和一台服务器计算机相邻。求服务器的最少数量。
下面两个例子:(a)是非法的,因为4同时和两台服务器相邻,而6不与任何一台服务器相邻。而图(b)是合法的。
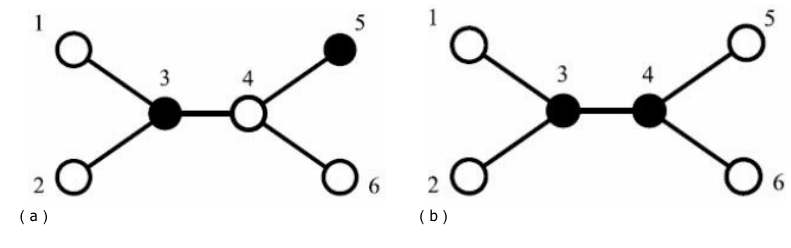
<解析>
这道题的状态就更为复杂——因为父节点影响子节点的状态总共3个,所以为了能够转移状态,我们需要在dp的第二维设置成3个状态。
dp[u][0]:节点u本身就是一个服务器;
dp[u][1]:节点u的父亲是一个服务器,但u不是;
dp[u][2]:节点u和u的父亲都不是服务器;
那么根据题目给出的条件——一个非服务器节点的相邻节点有且仅有1个节点是服务器。我们可以推论出:若u是服务器,则u的儿子可以是服务器也可以不是(状态0和1);若u不是服务器,但u的父亲是服务器,则由于u不能相邻两个服务器,u的儿子也一定不是服务器(状态2);若u的父亲和u都不是服务器,则由于u必须相邻一个服务器,u的儿子一定是服务器(状态0)。
状态转移方程式就像下面这样:
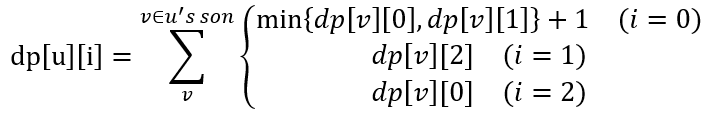
关键在定义状态,在方便转移的情况下尽可能的简洁!
就没有什么特别重要的了……😕
<源代码>

1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 using namespace std; 7 const int MAXN=10000,INF=int(1e7); 8 int n; 9 vector<int> lnk[MAXN+5]; 10 int dp[MAXN+5][3];//0: u is service ; 1: u's father is service ; 2: neither of u and its father is service 11 int DP(int u,int flag,int pre) 12 { 13 if(dp[u][flag]) return dp[u][flag]; 14 if(lnk[u].size()==1 && pre!=-1) 15 { 16 if(flag==2) return dp[u][flag]=INF; 17 return dp[u][flag]=!flag; 18 } 19 dp[u][flag]=0; 20 for(int i=0;i<(int)lnk[u].size();i++) 21 { 22 int v=lnk[u][i]; 23 if(pre==v) continue; 24 int A,B;A=B=INF; 25 switch(flag) 26 { 27 case 0: 28 A=DP(v,0,u); 29 B=DP(v,1,u); 30 break; 31 case 1: 32 A=DP(v,2,u); 33 break; 34 case 2: 35 A=DP(v,0,u); 36 break; 37 } 38 dp[u][flag]+=min(A,B); 39 } 40 dp[u][flag]+=!flag; 41 return dp[u][flag]; 42 } 43 int main(){ 44 //freopen("in.txt","r",stdin); 45 while(true) 46 { 47 memset(dp,0,sizeof dp); 48 memset(lnk,0,sizeof lnk); 49 scanf("%d",&n); 50 for(int i=1,u,v;i<n;i++) 51 scanf("%d%d",&u,&v), 52 lnk[u].push_back(v), 53 lnk[v].push_back(u); 54 int A=DP(1,0,-1); 55 int B=DP(1,2,-1); 56 int res=min(A,B); 57 printf("%d\n",res); 58 int tag;scanf("%d",&tag); 59 if(tag==-1) break; 60 } 61 return 0; 62 }
The End
Thanks for reading!
- Lucky_Glass



