【学时总结】◆学时·VII◆ 高维DP
◆学时·VII◆ 高维DP
自学之余,偶遇DP……
◇ 算法概述
顾名思义——一种处理多方面状态的DP,这种DP特点是……每一维的大小都不算太大(不然用dp数组存储下来内存会炸),而且枚举时容易超时……(一般来说,DP的复杂度为每一维的可取值之积。毕竟是乘积,很容易炸掉)。
众所周知,除了状压DP,一般的DP都是每一维表示了一个方面的状态,因此我们需要按照一定顺序枚举状态。
高维DP的大多数题中,各个方面的状态是互相关联、影响的,因此注意状态之间的互相限制是高维DP的难点,这也导致高维DP非常费脑子——状态转移方式奇多无比。
还有什么注意事项就看下面的例题吧~
◇ 例题选讲
(好像只找到一道题,之后找到其他的好题再补上吧……QwQ)
【Codeforces 14E】Camels +传送门+
· 题目大意
n个数依次为A1~n,当且仅当第i个数(1<i<n)满足 Ai-1<Ai 且 Ai>Ai+1 ,我们称Ai是一个驼峰;当且仅当 Ai-1>Ai 且 Ai<Ai+1 ,我们称 Ai 是一个谷底。已知 1≤Ai≤4 ,求恰好形成t个驼峰的方案数。
· 解析
这道题是DP没任何问题,统计类一般是DP(其他就是暴力DFS[补充 2018-08-09 08:04:21]以及组合数学推导公式)……
现在就可以开始找有哪些方面的状态了:
数的位置 i;第 i 个位置上的数 j ;第 i 个数在第 k 个驼峰上(从上升段开始到下降段结束);第 i 个数在驼峰的上升/下降段。
注意:我们并不需要找到所有的状态,那些关联很紧密(几乎一一对应的)就不需要用了,我们只需要找相对有独立性但仍能影响其他状态的状态。
有了这些状态,我们就可以进行状态转移了。
提示:如果你发现你找出的状态无法互相转移,不要犹豫,换一种方法吧……
分几种情况讨论(Tab. 这里将驼峰算作上升段,谷底算作下降段):
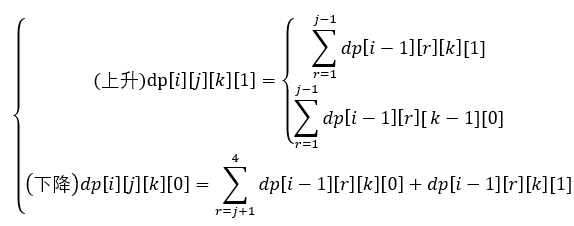
上升的第一种dp[i-1][r][k][1]就是i和i-1在同一个驼峰上且都处于上升段,直接相加;
上升的第二种dp[i-1][r][k-1][0]就是i-1是前一个驼峰上的下降段的末尾(谷底),直接相加;
下降的第一种dp[i-1][r][k][0]就是i-1和i在同一个驼峰上,都处于下降段,直接相加;
下降的第二种dp[i-1][r][k][1]就是i-1和i在同一个驼峰上,i-1处于上升段的末尾(驼峰),直接相加;
[补充 2018-08-09 16:09:51 - 由于一些reader不知道下面代码13~15行的初始化什么意思,这里加上]
由于题目规定最初的一段必须是上升的,为了避免下降的情况,我们从第2个数开始初始化,因为只有一个数时并看不出是上升还是下降,初始化第一个数显得没什么必要。dp[2][2][1][1]包含了 {1,2} ;dp[2][3][1][1] 包含了 {1,3},{2,3};dp[2][4][1][1] 包含了 {1,4},{2,4},{3,4} 。这样就保证了1~2的段上一定是上升的!
· 源代码
1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int MAXN=20,MAXDIG=4,MAXT=10; 7 typedef long long ll; 8 ll dp[MAXN+5][MAXDIG+5][MAXT+5][2]; 9 //dp[i][j][k][r] 第i个数为j时在第k个驼峰上处于 r=1上升,r=0下降 状态 10 int main() 11 { 12 int n,t;scanf("%d%d",&n,&t); 13 dp[2][2][1][1]=1; 14 dp[2][3][1][1]=2; 15 dp[2][4][1][1]=3; 16 for(int i=3;i<=n;i++) 17 for(int j=1;j<=4;j++) 18 for(int k=1;k<=t;k++) 19 for(int r=1;r<=4;r++) //上一个数字 20 { 21 if(r<j) 22 dp[i][j][k][1]+=dp[i-1][r][k][1]; 23 if(r<j && k>0) 24 dp[i][j][k][1]+=dp[i-1][r][k-1][0]; 25 if(r>j) 26 dp[i][j][k][0]+=dp[i-1][r][k][0], 27 dp[i][j][k][0]+=dp[i-1][r][k][1]; 28 } 29 ll ans=0; 30 for(int i=1;i<=4;i++) 31 ans+=dp[n][i][t][0]; 32 printf("%lld\n",ans); 33 return 0; 34 }
[补充 2018-08-09 20:44:09:作者终于找到一道好题了QwQ]
【UVA 10118】Free Candies +传送门+(Uva比较慢,这边是vjudge的链接)+传送门+
· 题目大意
有4堆糖果,每堆n个,糖果有不同的颜色。Little Bob有一个小篮子,可以装下5颗糖果。他每次可以拿出一堆糖果的顶部的糖果(一堆糖果拿完了就不能拿了)放进篮子里。每次取了糖果后,他会检查自己的篮子——如果里面有一对相同颜色的糖果,他就会取出那一对糖果放在自己的包里。
n不超过40,糖果的颜色用整数表示,该整数不超过20。
输入多组数据,每组数据第一行为n,以下n行每行4个整数,构成一个n行4列的矩阵,第i列自上至下描述了一堆糖果。输入以0结束。
计算最后Bob口袋里糖果最多有多少个,输出所得值除以2。
· 解析
由于n并不大,我们甚至能够储存一个n4的数组,于是我们就可以定义出DP状态——dp[pos[0]][pos[1]][pos[2]][pos[3]],其中pos[i]表示现在第i堆糖果的顶部是原来第i堆糖果的第几个。
这样就非常好转移——每一次只会取出4堆糖果中的一堆糖果的顶部。但是比较麻烦的是判断篮子里是否有同样颜色的糖果,用递推处理的话没法判断取出糖果的先后性(这道题中顺序会影响答案 ?留给reader们想一想)。比较好处理先后顺序的是DFS,于是我们想到可以用记忆化搜索!由于对于每一种剩余糖果的情况都唯一对应一种得到糖果数量,所以满足DP所需要的性质。
在记忆化搜索中,需要下传一个vis(用二进制压缩),表示当前篮子里有哪几种颜色的糖果,又因为同种颜色的糖果达到两个,Bob就会把他们拿出去,所以同种颜色的糖果不会超过1个,也就可以二进制压缩了。当vis中存在5个元素,则篮子满了,而里面没有相同颜色的糖果,返回0(不赋值给dp)。
每次枚举4堆糖果中的一堆,如果那堆糖果没有取完,就尝试取出堆顶,更新vis。
其他还有什么就看代码了……
· 源代码
1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int MAXN=40; 7 int n; 8 int cdy[MAXN+5][4],dp[MAXN+2][MAXN+2][MAXN+2][MAXN+2]; //糖果,以及DP数组 9 int pos[4]; //pos[i]表示现在第i堆糖果的顶部是原来的第pos[i]个糖果 10 int DP(int vis) 11 { 12 int fvis=vis,cnt=0; 13 while(fvis) cnt+=fvis%2,fvis/=2; //统计vis的元素数量,也就是篮子里的糖果数量 14 if(cnt>=5) return 0; 15 int A=pos[0],B=pos[1],C=pos[2],D=pos[3]; 16 if(dp[A][B][C][D]) return dp[A][B][C][D]; 17 for(int i=0;i<4;i++) 18 if(pos[i]<=n) //未取空 19 { 20 int x=1<<cdy[pos[i]][i]; //第pos[i]个元素的颜色 21 pos[i]++; //取出 22 if(vis&x) //vis中存在此种颜色 23 dp[A][B][C][D]=max(dp[A][B][C][D],DP(vis^x)+1); 24 else 25 dp[A][B][C][D]=max(dp[A][B][C][D],DP(vis|x)); 26 pos[i]--; //回溯 27 } 28 return dp[A][B][C][D]; 29 } 30 int main() 31 { 32 //freopen("in.txt","r",stdin); 33 while(~scanf("%d",&n) && n) 34 { 35 memset(dp,0,sizeof dp); 36 for(int i=1;i<=n;i++) 37 for(int j=0;j<4;j++) 38 scanf("%d",&cdy[i][j]); 39 pos[0]=pos[1]=pos[2]=pos[3]=1; //从堆顶开始取 40 printf("%d\n",DP(0)); //一开始篮子里什么都没有 41 } 42 return 0; 43 }
The End
Thanks for reading!
- Lucky_Glass


