【赛时总结】◇赛时·VI◇ Atcoder ABC-104
◇赛时·VI◇ ABC-104
◆???
莫名爆炸……ABC都AK不了 QwQ
C题竟然沦落到卡数据的地步;D题没有思路,直接放弃 ⋋( ◕ ∧ ◕ )⋌
◆ 题目&解析
◇A题◇ Rated for Me +传送门+
- 【题意】
给出比赛的场次;将场次小于1200的编为"ABC",场次大于等于1200小于2800的编为"ARC",场次大于等于2800小于4208的编为"AGC";输出编号。
- 【解析】
个人觉得不需要讲……题目读懂,if语句一写就好了……(萌新reader如果不太懂可以在文末邮箱email)
- 【源代码】
1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 int main() 7 { 8 int n;scanf("%d",&n); 9 if(n<1200) printf("ABC\n"); 10 else if(n<2800) printf("ARC\n"); 11 else printf("AGC\n"); 12 return 0; 13 }
◇B题◇ AcCepted +传送门+
- 【题意】
给出一个长度在4到10的字符串,一个字符串的结果为"AC"当且仅当 该字符串开头为大写A,从开头第3个字符到末尾第2个字符(包含)之间恰好存在一个大写C,除去‘A’、'C'两个字符,其余字符均为小写;否则结果为"WA"。输出对应字符串的结果。
- 【解析】
名副其实的英语阅读题……就因为一个题目没读懂WA了3遍 QwQ
先判断开头是否为A。定义bool变量F,标记从开头第3个字符到末尾第2个字符(包含)之间是否已经找到一个C,再扫描整个字符串,如果在从开头第3个字符到末尾第2个字符(包含)之外有大写字母(除了开头的A),则判为WA,若在正确区间内发现了C,就修改F为true,如果发现修改前F已经为true,说明C太多了,也判为WA。其余答案为AC。
- 【源代码】
1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 char str[20]; 7 int len; 8 int main() 9 { 10 scanf("%s",str); 11 len=strlen(str); 12 if(str[0]!='A') {printf("WA\n");return 0;} 13 bool F=false; 14 for(int i=0;i<len;i++) 15 if('A'<=str[i] && str[i]<='Z') 16 { 17 if(str[i]=='A' && i!=0) {printf("WA\n");return 0;} 18 if(str[i]=='C') 19 if(2<=i && i<=len-2) 20 { 21 if(F){printf("WA\n");return 0;} 22 else F=true; 23 } 24 else {printf("WA\n");return 0;} 25 if(str[i]!='A' && str[i]!='C') {printf("WA\n");return 0;} 26 } 27 if(!F){printf("WA\n");return 0;} 28 printf("AC\n"); 29 return 0; 30 }
◇C题◇ All Green +传送门+
- 【题意】
有D种题,第i种题有 Pi 个,每个分值为 100*i ,若将第 i 种题全部做完,会额外奖励 Ci 分。求要得到至少 G 分最少需要做多少道题。保证有解,且 G 和 Ci 是100的倍数。
- 【解析】 Tab:下面讲的不是正解
沦落到只能卡数据……
看到这道题的第一想法就是背包,一个特别的多重背包。状态定义非常标准化,dp[i][j] 表示前 i 种题获得至少 j 分的最小做题数。转移方程也很寻常,只是加了一个做完一种题的额外分的特殊处理(感谢ywk童鞋,下面修改了一个错误 2018-08-06 10:52:17):
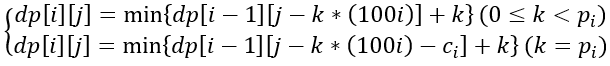
但是我们发现……题目的 G 竟然没有定义最大值,只说有解……
这就意味着dp[i][j]的第二维其实是会爆内存的。不可否认单纯的DP一定足够快,但是内存非常的感人。
但是我一意孤行要用DP的背包做这道题,于是 oh,一个STL的诡异容器从我的脑海中闪现了出来——映射 map !
众所周知 map 进行一次操作的时间复杂度为 O(logn) 无疑会减慢运行速度,但是它省空间啊!(时间换空间,oh my god)于是就可以愉快地DP了!一次AC,秀一下这心惊胆战的提交记录:

(2018-08-06 10:59:20 修正,再次感谢ywk童鞋)各位reader们当我上面什么都没说……好像G的最大值推出来连1e5都没有……所以是存得下的。那么这道题就是一个简单的背包了!不需要map!
- 【源代码】
1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<map> 6 using namespace std; 7 const int INF=int(1e9); 8 int n,goal; 9 int con[15][2]; 10 map<int,int>dp[15]; 11 int DP(int x,int y) 12 { 13 if(y<=0) return 0; 14 if(x<1) return INF; 15 if(dp[x].count(y)) return dp[x][y]; 16 dp[x][y]=INF; 17 for(int i=0;i<con[x][0];i++) 18 dp[x][y]=min(dp[x][y],DP(x-1,y-i*x)+i); 19 dp[x][y]=min(dp[x][y],DP(x-1,y-con[x][0]*x-con[x][1])+con[x][0]); 20 return dp[x][y]; 21 } 22 int main() 23 { 24 scanf("%d%d",&n,&goal); 25 goal/=100; 26 for(int i=1;i<=n;i++) 27 scanf("%d%d",&con[i][0],&con[i][1]),con[i][1]/=100; 28 printf("%d\n",DP(n,goal)); 29 return 0; 30 }
(2018-08-06 11:01:03 修正代码)
1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<map> 6 using namespace std; 7 const int INF=int(1e9); 8 int n,goal; 9 int con[15][2]; 10 int dp[15][int(1e5)]; 11 int DP(int x,int y) 12 { 13 if(y<=0) return 0; 14 if(x<1) return INF; 15 if(dp[x][y]!=-1) return dp[x][y]; 16 dp[x][y]=INF; 17 for(int i=0;i<con[x][0];i++) 18 dp[x][y]=min(dp[x][y],DP(x-1,y-i*x)+i); 19 dp[x][y]=min(dp[x][y],DP(x-1,y-con[x][0]*x-con[x][1])+con[x][0]); 20 return dp[x][y]; 21 } 22 int main() 23 { 24 memset(dp,-1,sizeof dp); 25 scanf("%d%d",&n,&goal); 26 goal/=100; 27 for(int i=1;i<=n;i++) 28 scanf("%d%d",&con[i][0],&con[i][1]),con[i][1]/=100; 29 printf("%d\n",DP(n,goal)); 30 return 0; 31 }
◇D题◇ We Love ABC +传送门+
- 【题意】
给出一个字符串S,仅包含 'A','B','C'和'?' 。你可以(也必须)把'?'替换成'A'~'C'的任意一个字母,对于每一种替换全部完成的情况,计算满足下列条件的三元组(i,j,k)数量:
i<j<k,S[i]='A',S[j]='B',S[k]='C'。
统计总和。
- 【解析】
考虑没有'?'的情况,对于S的第i个字符,统计开头到第i-1个字符中A的个数(a[i])以及从i+1到末尾C的个数(c[i]),若 S[i]='B',则有 若选取第 i 个字符(作为中心的B),方案数为 a[i]*c[i] ,即 i 之前的每一个A都可以与 i 后面的C配对,形成一种答案(乘法原理)。所以我们只需要对 S 中的每一个B进行这样的一次计算,统计总和即可。
但是现在有'?',我们再统计开头到i-1的'?'的数量(kn_fro[i]),以及从i+1到末尾'?'的数量(kn_beh[i])。考虑下面3种情况:
(1) 将i之后的一个?变成C,与i前面的一个A配对,其余?任意变换。则配对的方案数为 a[i]*kn_beh[i](乘法原理,前面的每一个A都可以与后面的每一个?配对),而其余?任意变换的方案数为 3kn_fro[i]+kn_beh[i]-1,即剩余 (kn_fro[i]+kn_beh[i]-1)个?,每一个都可以换成 A~C 的任意一个。方案数为:
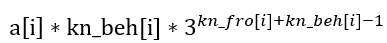
(2) 将i之前的一个?变成A,与后面的一个C配对,其余?任意变换……与(1)一样,方案为:

(3) 将i之前的一个?变成A,再把后面的一个?变成C,再将变换之后的A和C配对,其余乱选。选择A和C的方案为 (kn_fro[i]*kn_beh[i]),其他乱选的方案为(3kn_fro[i]+kn_beh[i]-2)——这次是有两个?已经固定,因此需要-2。方案数为:
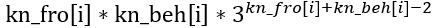
需要对哪些字符统计这样的值呢?
首先原来是B的字符一定要统计,当然还有每一个?,因为我们可以将那一个?固定变成B。
统计答案即可(标程好像是DP……我觉得没必要)
- 【源代码】
1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 typedef long long ll; 7 const ll MOD=ll(1e9)+7; 8 const int MAXN=int(1e5); 9 ll Pow3[MAXN+5]; 10 char S[MAXN+5]; 11 ll a[MAXN+5],c[MAXN+5],kn_fro[MAXN+5],kn_beh[MAXN+5]; 12 int main() 13 { 14 ll f=1; 15 for(int i=0;i<=1e5+2;i++) Pow3[i]=f,f*=3ll,f%=MOD; //预处理3的次方 16 scanf("%s",S);int len=strlen(S); 17 for(int i=0,totA=0,totkn=0;i<len;i++) //统计a[i],kn_fro[i],均不包含第i个字符本身 18 { 19 a[i]=totA;kn_fro[i]=totkn; 20 if(S[i]=='A') totA++; 21 if(S[i]=='?') totkn++; 22 } 23 for(int i=len-1,totC=0,totkn=0;i>=0;i--) //统计c[i],kn_beh[i],均不包含第i个字符本身 24 { 25 c[i]=totC;kn_beh[i]=totkn; 26 if(S[i]=='C') totC++; 27 if(S[i]=='?') totkn++; 28 } 29 ll ans=0; 30 for(int i=0;i<len;i++) 31 if(S[i]=='?' || S[i]=='B') 32 { //这里一些玄学错误……如果大家发现只在第11组数据WA了,肯定是long long 炸了,把MOD的顺序换一下再交吧…… 33 ll O1=a[i]*((c[i]*Pow3[kn_beh[i]+kn_fro[i]])%MOD)%MOD, //A->C 34 O2=kn_beh[i]? (a[i]*(kn_beh[i]*Pow3[kn_beh[i]+kn_fro[i]-1]%MOD)%MOD):0ll, //A->? 35 O3=kn_fro[i]? (c[i]*(kn_fro[i]*Pow3[kn_fro[i]+kn_beh[i]-1]%MOD)%MOD):0ll, //?->C 36 O4=(kn_beh[i] && kn_fro[i])? (kn_fro[i]*(kn_beh[i]*Pow3[kn_fro[i]+kn_beh[i]-2]%MOD)%MOD):0ll; //?->? 37 ll Sum=((O1+O2)%MOD+(O3+O4)%MOD)%MOD; 38 ans+=Sum; 39 ans%=MOD; 40 } 41 printf("%lld\n",ans); 42 return 0; 43 }
◆ 涨Rating啦!

The End
Thanks for reading!
- Lucky_Glass
(Tab:如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我,在周末我会尽量解答并完善博客~)


