【例题收藏】◇例题·III◇ 木と整数 / Integers on a Tree
◇例题·III◇ 木と整数 / Integers on a Tree
只需要一个美妙的转换,这道题就会变得无比美妙……
◆ 题目大意
给定一棵n个节点(节点被编号为1~n)的树,有K (1≤K≤n) 个节点已经被填上一个数字,现在你需要把剩余的节点填上数字,使得被同一条边相连的两个节点数值相差恰好为1。
若可以实现,先输出一行"Yes",接下来n行,每行输出一个整数,第i+1行表示节点i的数值;否则输出"No"。
若最初填上的数值没有满足相连两点差为1,也判定为No。
◆ 解析
这道题的解法非常美妙~
首先我第一个思路是BFS。一个很简单的结论,每向外延伸一个节点,节点的可取值就会增加2——最大值增加1,最小值减小1。这是很直观的:

于是我储存了每一个节点的可取值范围 [最小值,最大值] ,由于一些点已经给出值,这些点的最大值等于最小值。
另外一个简单结论就是——相邻节点的奇偶性相反(就不证明了)
于是我把已经固定值的节点作为起点:初始化它的最大值、最小值为它的定值;把它push进队列里。
利用BFS,从已知取值范围为[Au,Bu]的点u向外扩展到点v,若v没有确定范围,则v的范围暂时确定为[Au-1,Bu+1];若已经确定范围为[Av,Bv],则先判断点v的奇偶性是否冲突(只需要判断最大值或最小值的奇偶性是否冲突就可以了[为什么?想一想就知道了!]),若冲突,则直接输出"No",否则更新v的范围为[max{Av,Au+1},min{Bv,Au-1}],若v的取值范围为空(最大值小于最小值),则输出"No"。
最后遍历一遍树,就可以得到所有点的取值了……
唠了这么多……其实这个想法Wa了 QwQ
(肯定被打 @( ◕ x ◕ )@)
下面是正解……
若两点u,v满足v的数值小于u,且u,v之间有满足条件的解,则u到v的路径上的节点的数值存在两种情况:
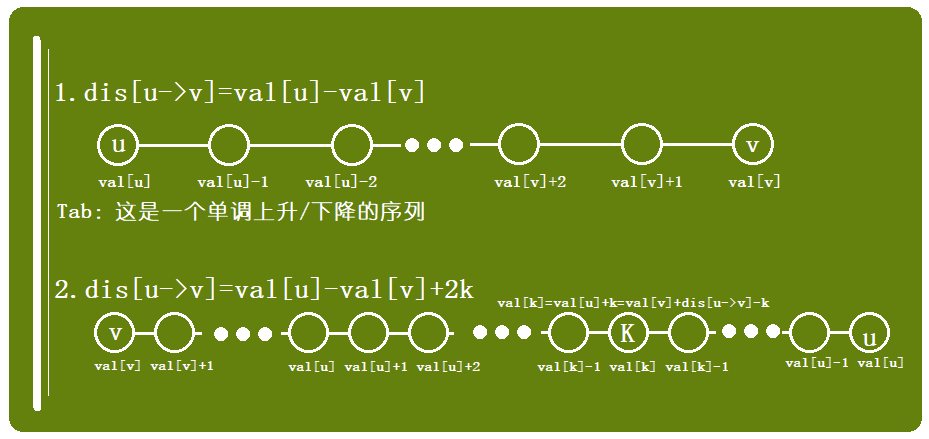
扩展到多个点也是满足的。
如何实现?
定义一个优先队列(小根堆),按节点的数值为关键字排序。我们可以把优先队列的类型定为 pair<int,int> ,因为pair<>的大小关系只取决于第一个元素(.first),所以我们把节点的值作为first,节点编号作为second,就可以实现按数值为关键字排序。同时定义答案数组 ans[]。先把已知节点的答案定为已知值,并push入队列。
每次取出队列的开头,也就是已知值最小且仍可能更新其他节点值的节点。以该节点u为起始点向它相连的点v更新,若ans[v]没有赋值,则直接赋为ans[v]=ans[u]+1;否则判断 |ans[v]-ans[u]| 是否等于1,不满足则输出No。
其他的就请详见代码了~
◆ 源代码
1 /*Lucky_Glass*/ 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #include<queue> 7 #include<cmath> 8 using namespace std; 9 const int MAXN=int(1e5),INF=int(1e9); 10 vector<int> lnk[MAXN+5]; 11 //邻接表储存图 12 priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > que; 13 //定义小根堆,first为节点数值,second为节点编号 14 int ans[MAXN+5]; 15 //储存已知值 16 int n,m; 17 int main() 18 { 19 scanf("%d",&n); 20 for(int i=1,u,v;i<n;i++) 21 scanf("%d%d",&u,&v), 22 lnk[u].push_back(v), 23 lnk[v].push_back(u); 24 scanf("%d",&m); 25 fill(ans,ans+MAXN+5,INF); //初始化 26 for(int i=0,x,y;i<m;i++) 27 scanf("%d%d",&x,&y), 28 que.push(make_pair(y,x)), //将已知节点push进队列 29 ans[x]=y; 30 while(!que.empty()) 31 { 32 int u=que.top().second,val=que.top().first; //取出已知值最小且可能更新周围节点的节点 33 /*什么叫可能更新周围节点?每一次更新一定会更新完一个节点的全部相邻节点,且这些节点不再更新,因此每一个节点在队列里只出现一次*/ 34 que.pop(); 35 for(int i=0;i<lnk[u].size();i++) 36 { 37 int v=lnk[u][i]; 38 if(ans[v]==INF) 39 ans[v]=val+1,que.push(make_pair(ans[v],v)); //更新值 40 if(fabs(ans[v]-ans[u])!=1) //不满足条件 41 { 42 printf("No\n"); 43 return 0; 44 } 45 } 46 } 47 printf("Yes\n"); 48 for(int i=1;i<=n;i++) 49 printf("%d\n",ans[i]); 50 return 0; 51 }
The End
Thanks for reading!
- Lucky_Glass


