【学时总结】 ◆学时·II◆ IDA*算法
【学时·II】 IDA*算法
■基本策略■
如果状态数量太多了,优先队列也难以承受;不妨再回头看DFS……
A*算法是BFS的升级,那么IDA*算法是对A*算法的再优化,同时也是对迭代加深搜索(IDFS)的优化。之前的学习中,已经了解到A*算法通过启发函数达到了有效的优化,而迭代加深搜索则通过限制搜索深度,成功地避免了无止境的向下搜索而无解的情况。
现在学习的IDA*算法则是将前两种结合,限制搜索深度,若当前深度加上启发函数预估值(乐观估算:估计值<=实际值)已经大于深度限制,则终止搜索,然后不断放松限制,得到第一个解就是最优解。IDA*的函数通常以bool作为返回值,一方面代替了全局变量flag的判断是否已经找到解的作用,另一方面,更方便地使整个DFS在找到解后迅速退出。
至于为什么要用IDA*算法?其实我们需要弄懂A*和IDA*算法的本质——分别是BFS和DFS。
①BFS具有的优点是同时考虑所有情况,不会错误地搜到底,且能一次找到正解;但是缺点也很明显,就是占用空间。
②DFS具有的优点是只占用栈空间,不需要以任何数据结构为依靠;但缺点也提到:如果当前的这个路线是错误的,他会一直搜到底,直到返回,浪费时间,且第一次找到的不一定是最优解;
当DFS加上深度限制,它更像BFS了——由于深度限制就是限制了它的代价,所以它第一次找到的接就是代价最小解;也由于这个限制,它避免了错误地一直往下搜。但是传统的迭代加深搜索并不是太优,所以我们又提出了启发函数,是一个“乐观”地预估剩余代价的函数,找到一个小于等于实际代价的花费。如果当前花费加上预估花费都超过限制,就提前结束搜索。
■一些例题■
其实就是迭代加深搜索 ๑乛◡乛๑
◆凡事要先从水题开始◆ DNA sequence
- HDU 1560
- 解析
这其实是一个很基础的匹配问题——序列匹配。序列就不一定连续,所以我们只需要判断当前字母是否与下一个需要匹配的字母相同就可以了。我们可以定义一个指针变量来指向各个序列下一个需要匹配的位置,每次添加一个字母后判断其是否可以与下一个字符匹配,如果可以匹配就后移指针。
这一点很好理解,但后面就要难一些了。我们先考虑启发函数:
A:D()为当前的深度;H()为当前未匹配序列的最大长度(比如现在有"ATG","T","GA"未匹配,则H()=3);定义启发函数G()=H()+D()。
评价:因为要让序列匹配,首先需要满足字母的个数,所以这个函数一定是正确的;
B:D()为当前深度;令A[i],C[i],G[i],T[i]方便表示ACGT在第i个序列中未匹配的序列里的个数,则启发函数\(G()=\max A[k_1]+\max B[k_2]+\max C[k_3]+\max D[k_4]\)(比如未匹配序列为"ACA","GG","ACG",则max A[]=2,max G[]=2,max C[]=1,所以G()=5)
评价:比上一个函数更优,更准确
接下来就是一个贪心的思想——如果现在存在一个答案与所有序列匹配,但是其中有一个字母不与任何一个序列匹配,则删除该字母后,答案依然成立,所以原答案不是最优的。虽然枚举4种字符的复杂度也不高,但是仍然可以优化。
最后注意回溯的细节,不要把本来就没有匹配的序列回溯,也不要少回溯匹配的序列!
- 源代码
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,depth;
int len[10],chr[10][4],mat[10];
char DNA[10][10];
inline int GetPri()
{
int ret=0;
for(int j=0;j<4;j++)
{
int Max=0;
for(int i=0;i<n;i++)
Max=max(Max,chr[i][j]);
ret+=Max;
}
return ret;
}
bool ID_A_Star(int dep)
{
int pri=GetPri();
if(dep+pri>depth) return false;
if(!pri)
return true;
for(int i=0;i<4;i++)
{
char ch=i+'0';bool chg[10]={},flag=true;
for(int j=0;j<n;j++)
if(DNA[j][mat[j]]==ch)
chr[j][DNA[j][mat[j]]-'0']--,mat[j]++,chg[j]=true,flag=false;
if(!flag)
if(ID_A_Star(dep+1))
return true;
for(int j=0;j<n;j++)
if(chg[j])
mat[j]--,chr[j][DNA[j][mat[j]]-'0']++;
}
return false;
}
int main()
{
int t;scanf("%d",&t);
while(t--)
{
memset(DNA,'\0',sizeof DNA);
memset(chr,0,sizeof chr);
memset(len,0,sizeof len);
memset(mat,0,sizeof mat);
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%s",DNA[i]);
len[i]=strlen(DNA[i]);
for(int j=0;j<len[i];j++)
switch(DNA[i][j])
{
case 'A': DNA[i][j]='0';chr[i][0]++;break;
case 'C': DNA[i][j]='1';chr[i][1]++;break;
case 'G': DNA[i][j]='2';chr[i][2]++;break;
case 'T': DNA[i][j]='3';chr[i][3]++;break;
}
}
depth=GetPri();
while(!ID_A_Star(0))
{
memset(mat,0,sizeof mat);
depth++;
}
printf("%d\n",depth);
}
return 0;
}
◆是时候进阶了◆ The Rotation Game
- HDU 1667
- 解析
- 数据结构
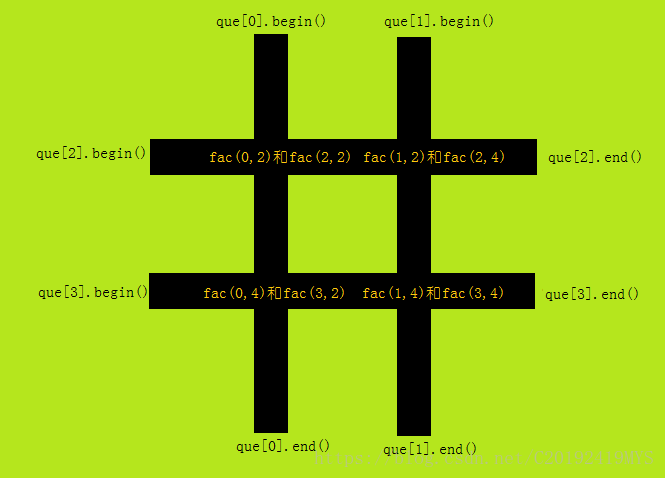
这道题的第一个考点就是数据储存,虽然我知道可以暴力地用2维矩阵储存,但是在这里我还是更为推荐STL的一个容器——deque,即双端队列——支持插入或删除队首、队尾的元素的队列。
我们可以将“#”的4条树链分别储存为一个队列。由于deque是无法直接修改内部元素的,这里就运用到了迭代器——deque<int>::iterator,一个类似于指针的东西。它十分有效,由于deque的基础数据结构是链表,我们可以通过类似于que.begin()+k的形式来得到que里第k(k从0开始)个元素的迭代器,相当于que[i],且复杂度仅为\(O(1)\)。那么我就写了一个函数 fac(x,y) 表示第x个队列中第 y 个元素的迭代器。
那么有了迭代器我们就可以直接修改变量的值了——定义deque<int>::iterator it=fac(x,y),那么直接用*it=var就可以了。
2. 操作实现
我们这里把‘#’编号如下:
由于一次操作会牵连到3个队列,例如'A',会影响que[0]、que[2]、que[3]。所以我手打了mov[i]为操作 i+'A' 的方法:
mov[i][0]:操作将会旋转哪一个队列;
mov[i][1]:相当于bool,当为 false,则队首转移到队尾,为 true 则队尾转移到队首;
mov[i][2]:将会影响的第一个队列编号;
mov[i][3]:将会影响到队列 mov[i][2] 的第几个元素;
mov[i][4]:将会影响到的第一个队列的元素进行操作后会变为队列 mov[i][0] 中的第几个元素;
mov[i][5]:将会影响的第二个队列编号;
mov[i][6]:将会影响到队列 mov[i][5] 的第几个元素;
mov[i][7]:将会影响到的第二个队列的元素进行操作后会变为队列 mov[i][0] 中的第几个元素;
我知道看起来极其复杂……不如举个例子:mov[0]是操作A,它会旋转队列0,由队首到队尾,将会影响队列2的第2个元素,旋转后的值为队列0的第2个元素,还会影响队列3的第2个元素,旋转后的值为队列0的第4个元素。所以 mov[0]={0,0,2,2,2,3,2,4}。嗯哼?٩(◕‿◕。)۶
根据上面的这个数组我就写成了Move函数。
3. IDA*
前面做完现在就简单了。先看启发函数——由于一次操作最多只能使中间8个格子中新增加一个相同元素,则设中间8格最多的元素个数为k,所以最少还需要 8-k 的操作。我们可以统计3种元素在中间格内的个数,再用8减其中的最大值就得到了启发函数。
这里在回溯时还有一个小技巧——dis[i]表示操作i的反操作,比如A的反操作为F。所以回溯时只需要执行一次反操作就可以了。
- 源代码
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
using namespace std;
const int ipt[][3]={{1,0},{1,1},{1,0},{1,1},{1,2},{1,2},{2,0,2},{1,2},{2,1,2},{1,2},{1,2},{1,0},{1,1},{1,3},{1,3},{2,0,3},{1,3},{2,1,3},{1,3},{1,3},{1,0},{1,1},{1,0},{1,1}};
const int mov[][8]={{0,0,2,2,2,3,2,4},{1,0,2,4,2,3,4,4},{2,1,0,2,2,1,2,4},{3,1,0,4,2,1,4,4},{1,1,2,4,2,3,4,4},{0,1,2,2,2,3,2,4},{3,0,0,4,2,1,4,4},{2,0,0,2,2,1,2,4}};
const int dis[8]={5,4,7,6,1,0,3,2};
//1 last-first 0 first-last
deque<int> line[4];
int depth;
char ans[107];
inline deque<int>::iterator fac(int x,int y)
{
deque<int>::iterator ret=line[x].begin()+y;
return ret;
}
int Get_Pri()
{
int tot[4]={};
tot[*fac(0,2)]++;tot[*fac(2,3)]++;tot[*fac(1,2)]++;
tot[*fac(0,3)]++; tot[*fac(1,3)]++;
tot[*fac(0,4)]++;tot[*fac(3,3)]++;tot[*fac(1,4)]++;
return 8-max(max(tot[1],tot[2]),tot[3]);
}
void Move(int knd)
{
if(mov[knd][1])
{
int last=line[mov[knd][0]].back();
line[mov[knd][0]].pop_back();
line[mov[knd][0]].push_front(last);
}
else
{
int first=line[mov[knd][0]].front();
line[mov[knd][0]].pop_front();
line[mov[knd][0]].push_back(first);
}
*fac(mov[knd][2],mov[knd][3])=*fac(mov[knd][0],mov[knd][4]);
*fac(mov[knd][5],mov[knd][6])=*fac(mov[knd][0],mov[knd][7]);
}
bool ID_A_Star(int dep)
{
int pri=Get_Pri();
if(dep+pri>depth) return false;
if(!pri) return true;
for(int i=0;i<8;i++)
{
ans[dep]=i+'A';
Move(i);
//Debug();
if(ID_A_Star(dep+1)) return true;
Move(dis[i]);
ans[dep]='\0';
}
return false;
}
int main()
{
while(true)
{
for(int i=0;i<4;i++) line[i].clear();
char ipts[105]="";gets(ipts);
if(ipts[0]=='0') break;
for(int i=0,j=0;i<24;i++,j+=2)
for(int k=1;k<=ipt[i][0];k++)
line[ipt[i][k]].push_back(ipts[j]-'0');
depth=0;memset(ans,'\0',sizeof ans);
//Debug();
while(!ID_A_Star(0))
depth++;
if(!depth) printf("No moves needed\n");
else cout<<ans<<endl;
cout<<*fac(0,2)<<endl;
}
return 0;
}
The End
Thanks for reading!
-Lucky_Glass