「SOL」JOISC2021 解题报告
JOIS(egment-Tree)C
1. 前言
很早之前教练让我们做这套题，我以为这套题应该挺简单，用几天的空余时间就能刷完，结果预想的短周期刷题变成了长周期刷题……（好像是整个团队里最后一个刷完的？？）
大多数题目（除了「保镖」和「特技飞行」，我不知道把特技飞行这种题放 Day1 是不是想搞选手心态 QwQ）还是能够独立地想出来，但是代码长度堪忧，看了一下好像每道题的代码都比其他人要长一些，不知道是不是实现细节的问题。话说过来虽然代码要长一些，但是运行效率好像要快一些耶，目前「IOI 热病」和「最差记者 4」都是 LOJ 的速度榜一 awa。
这一发是把线段树给练爽了，真就 JOI Segment-Tree Camp 呗。
2. Day1 解析
2.1. IOI 热病
2.1.1. 评析
推导「每个人行走方向其实固定」这一点比较考察贪心构造的技巧。
而后面「李超线段树上查全局最小值，支持删除坐标」这个有一定套路（我自己的做法，可能比较复杂），但是主要还是考察代码实现能力。
2.1.2. 解析
先枚举第一个人往哪个方向走，然后对其他人的最优行走方向进行分析。
不妨设 ta 向上走，先考虑一些特殊的位置——考虑到能一个人与一个人相遇的人是米字格形状的，所以先分析以起点为中心的米字格形状。
- 显然 1 区域只能向下，5 区域只能向上。
- 分析 2 区域，首先不可能向右向上；若向下，有一个非常巧妙的分析是「在时刻 \(i\) 出现感染的范围是距离起点横纵坐标之差不超过 \(i\) 的位置」，手动模拟一下「可能出现感染的范围」和 2 区域的人行走的情况，发现不可能被感染；于是只能向左。同理 8 区域只能向右。
- 分析 3 区域，不可能向右向下；若向上，同样模拟「可能出现感染的范围」和 3 区域行走的情况，不可能感染，所以只能向左。同理 7 区域只能向右。
- 分析 4 区域，不可能向右向下；若向左，同样模拟「可能出现感染的范围」和 4 区域行走的情况，发现只能向上。同理 6 区域只能向上。
分析得到这些区域只可能向一个方向走，于是我们大胆猜测其他区域也是这样。实际上利用「可能出现感染的范围」的分析同样可以得到以下结论：
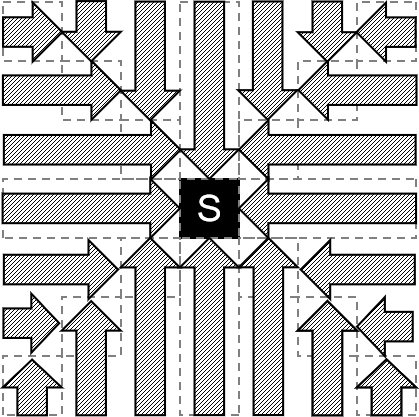
于是可以直接枚举第一个人走的方向，然后固定其他人走的方向。
接下来其实就是模拟感染的过程了。两个人相遇时可能会发生感染，但是必须要有一个人已经感染。记 \(d_i\) 表示第 \(i\) 个人被感染的时刻。则在 \(\ge d_i\) 的时刻，第 \(i\) 个人才具备感染能力。发现 \(d_i\) 其实就是最短路。
考虑用 Dijkstra 求最短路，设当前点为 \(u=(x_u,y_u)\)。不妨设 \(u\) 的行走方向为 \(y\) 正方向（即「向上」），\(u\) 能够更新到的点只有：
- 左上右上的对角线上的人，若这个人在 \(v=(x',y')\)，则相遇时间为 \(|x'-x_u|\)，当 \(|x'-x_u|\ge d_u\) 时会感染，更新 \(|x'-x_u|\overset \min\to d_v\)；
- \(u\) 行走方向上的人 \(v=(x_u,y')\)，则相遇时间为 \(\frac {y'-y_u}2\)，当 \(\frac {y'-y_u}2\ge d_u\) 时会感染，更新 \(\frac {y'-y_u}2\overset \min\to d_v\)；
我们发现每次更新，都是将对角线上或同行同列上，\(x\) 坐标（或 \(y\) 坐标）在某个范围内的点的 \(d\) 更新为一个关于 \(x\) 或 \(y\) 的一次式。于是可以对每条对角线、每行每列维护一棵李超线段树，每次区间插入一条直线，支持查找全局最小点。一个区间的最小点一定在端点取到，直接更新即可。
这样更新是支持了，但是 Dijkstra 还需要「弹出当前点」，也就是将当前这个 \(d\) 最小的点删除。李超线段树不是不支持删除吗？李超线段树不支持删除已经插入的直线，但是可以删除要考虑的点。我们可以给已经删除的点打标记，更新区间最小值时找到左右两端的未被删除的点，这种「只有删除，查找下一个未删除的点」的操作实际上是一个并查集的套路。
可能就是并查集运行效率非常高，使我的代码运行速度比其他人要快吧。
时间复杂度瓶颈在于李超线段树区间插入线段，\(\mathcal O(n\log^2n)\)，常数较大。
2.1.3. 源代码
考虑到直接粘贴代码会使文章长度爆炸，这里直接附上 LOJ 的提交记录。
> Link LOJ - IOI热病 参考代码
2.2. 饮食区
2.2.1. 评析
部分分算法特别多，比较考验选手对各种算法的熟悉程度。
一开始我想的是分块，然后空间卡不过去……
2.2.2. 解析
删除操作非常麻烦。如果没有删除操作，那么我们可以整体二分，对每个查询找到第一次队列的人数大于等于 \(B_i\) 的时候。
考虑删除会产生什么影响。我们尝试「不真的进行删除操作」，而是把查询给定的位置 \(B_i\) 向后移动离开的人数。注意到队列可能小于 \(K_i\)，不能直接向后移动 \(K_i\)。
用线段树分别维护「不考虑删除操作，当前队列有多少人」，以及「考虑删除操作，当前队列有多少人」。第一种就是区间加、单点查；第二种稍麻烦，每次有删除操作时，需要全部元素对 \(0\) 取 \(\max\)，但是只涉及单点查询，可以直接维护形如 \(x'=\max\{x+a,b\}\) 的懒标记 \((a,b)\)，而不用 Segment Tree Beats! 。
两个值的差就是询问前离开的人数，然后就可以整体二分了。注意需要提前判断是否无解。
时间复杂度 \(\mathcal O(n\log^2n)\)。
2.2.3. 源代码
> Link LOJ - 饮食区 参考代码
3. Day2 / Day3 解析
因为通信题暂时不做，然后「保镖」这道题又完全不会，Day2Day3 就合起来了……
3.1. 道路建设
3.1.1. 评析
这道题硬上复杂数据结构（树套树、KD树）也能做，但是在考场上比较消耗时间。
如果多花些时间思考有没有简单一些的方法，反而可能节省时间。毕竟出题人只要不是想要出防 AK 题会考虑代码的复杂程度。
3.1.2. 解析
显然是要用数据结构直接维护当前花费最小的方案，支持把最小的方案删除。
还是比较常见的套路，对每个点求出从它出发的最优方案，全部塞进堆里。每次从堆里取出全局最优方案，将其删除后找到对应点的次优方案。
曼哈顿距离有两个绝对值，如果硬上数据结构就需要树套树维护四个象限的点。但是题目规定起点终点交换本质相同，我们可以直接把点按 \((x,y)\) 双关键字排序，只考虑从较大的点出发到较小点的路径。这样一来 \(x\) 的绝对值就没了。
现在的问题就是维护 \((x,y)\lt(x_u,y_u)\) 的所有点中，\(y\) 在某个区间上的点的 \(\max\{-x-y\}\) 以及 \(\max\{-x+y\}\)。需要支持删除指定的点。
不管删除操作，那就是可持久化线段树。加上删除操作呢？那还是可持久化线段树，只在当前线段树上删除指定节点，把对应位置赋值为 \(-\infty\) 即可。
时空复杂度为 \(\mathcal O((n+K)\log n)\)。
3.1.3. 源代码
> Link LOJ - 道路建设 参考代码
3.2. 聚会 2
3.2.1. 评析
个人认为是一道比较一般的题目……仅仅是考察基础的树上信息维护的方法而已。
3.2.2. 解析
设出席者的点集为 \(S\)，通过调整法（如果「开会地址」不符合下述条件，可以通过把它向某个方向调整，使代价不减，直到符合下述条件，即为代价最小的「开会地址」）可证明：
- 若 \(|S|\) 为偶数，则「开会地址」可以取某条路径上的所有点；
- 若 \(|S|\) 为奇数，唯一的「开会地址」是 \(S\) 中距离其他点距离之和最小的点。
所以我们只需要回答 \(|S|\) 为偶数的的情况。不妨枚举上述的「某条路径」为 \((u,v)\)，
\(S\) 可取的点集为 \(\{u,v\}\cup S_1\cup S_2\)，并且 \(S\) 在 \(\{u\}\cup S_1\) 中的点数必须和 \(\{v\}\cup S_2\) 中的点数相等，类似于中位数。于是 \(dist(u,v)\) 可以贡献到 \(|S|\le2(\min\{|S_1|,|S_2|\}+1)\) 的所有偶数 \(|S|\) 的答案。
考虑树形 DP，\(f(u,s)\) 表示 \(u\) 子树内，子树大小大于等于 \(s\) 的最深的点的深度。一边转移一边贡献到答案。\(s\) 不超过 \(u\) 的子树大小，可以考虑 Dsu on Tree 进行优化，时间复杂度 \(\mathcal O(n\log n)\)。
但是我们发现 Dsu on Tree 只能计算「折线型」的路径，而不能计算祖先到后继的路径。分别考虑较小值在后继方向和在祖先方向的情况：
- 后继的子树较小：在 DFS 时，用线段树维护子树大小大于后继子树的祖先的最小深度，或者利用单调性二分；
- 祖先的子树较小：直接线段树合并维护出当前子树内，子树大小在某个区间内的后继的最大深度。
复杂度仍然是 \(\mathcal O(n\log n)\)。
3.2.3. 源代码
> Link LOJ - 聚会 2 参考代码
4. Day4 解析
4.1. 活动参观 2
4.1.1. 评析
考察了非常经典的字典序的贪心性质以及选手选择算法的能力。
与道路建设一题相同，用较简单的算法往往可以节省大量时间。
4.1.2. 解析
先读对题，字典序是将参加的活动按编号排序后再比较，而不是按参加时间比较。
于是贪心地从小到大判断「是否可以参加第 \(i\) 个活动」。
假设要参加，首先 \(i\) 不能和已经参加的活动冲突。
然后 \(i\) 会把原来的一个空闲时间段 \([L,R]\) 分成两段 \([L,l_i],[r_i,R]\)，记只考虑时间段 \([L,R]\)，最多能够参加的活动数量为 \(f(L,R)\)。则原本 \([L,R]\) 提供 \(f(L,R)\) 的贡献，现在只能提供 \(f(L,l_i)+f(r_i,R)+1\) 的贡献。直接判断剩余次数是否足够即可。
怎么计算 \(f(L,R)\)？贪心地选取活动，每次选取可参加的右端点最小的活动，于是参加一个活动之后的下一个活动（的右端点）是唯一的，倍增即可。
4.1.3. 源代码
> Link LOJ - 活动参观 2 参考代码
4.2. 最差记者 4
4.2.1. 评析
一道不错的线段树合并优化 DP 的题，对这个技巧比较熟练的话应该能一眼看出来。
如果想到利用 DP 数组的单调性维护差分数组，可以在一定程度上简化代码，但是没想到这点也能做。
4.2.2. 解析
把选手的 rating 的 “≥” 关系建为有向图，\(u\to v\) 表示 \(u\) 的 rating 小于等于 \(v\) 的 rating。
每个点的入度为 \(1\)，显然每个连通块是叶向基环树，不同连通块之间没有影响。基环树环上的点的 rating 必须相同，显然最终环的 rating 只可能是 \(1\) 或者环上某个点原本的 rating。
最后枚举环的取值，考虑对树的部分进行 DP。定义一个非常暴力的 DP 状态，\(f(u,w)\) 表示 \(u\) 的 rating 设为 \(w\)，子树内的总花费的最小值。
然而这样定义会使得 \(f(u,w)\) 有值的点很多，并且被分成前后缀两个部分。考虑到 \(c_i\) 之和为定值，我们可以反过来定义 \(f(u,w)\) 为 \(u\) 取 \(w\)，\(u\) 子树内减免的花费的最大值。
这样比较方便之后线段树合并。
转移式中有后缀 \(\max\)，并且是子树求和合并的形式，可以用线段树合并。我们发现，后缀 \(\max\) 使得大多数位置都有值，如果在合并是直接新建节点下放懒标记，会导致线段树节点数爆炸，破坏线段树合并的时间复杂度。但是后缀 \(\max\) 改变的位置数量只有子树大小，称改变的位置为「关键点」，则只需要维护关键点的值即可。
比较显然的是 \(v_1,v_2\) 合并后的关键点就是 \(v_1,v_2\) 各自的关键点的并，于是在合并时维护两棵线段树各自的后缀 \(\max\) 即可。合并时若出现一棵线段树已经为空，会对另一棵线段树产生「整体加上后缀 \(\max\)」的贡献，这意味着要打加法标记。我们并不希望下放标记，还好加法标记比较简单，可以采用标记永久化。
整个代码最复杂的部分就是线段树合并的函数，具体可以参考代码。
4.2.3. 源代码
> Link LOJ - 最差记者 4 参考代码
