「SOL」序列 (LOJ/NOI2019)

准备写新博客的时候发现自己草稿箱里还有一篇咕了十几天的题解 😦

思路挂在了费用流之前……

题面

> Link LOJ #3158

解析

这道题的本质是一个二分图带权匹配的问题，一个经典的做法是直接做费用流。

考虑如何在流网络中体现限制。只能选择恰好 \(K\) 对非常简单，只需要控制总流量为 \(K\) 即可；主要是 \(L\) 的限制。网络流并不容易限制下界，所幸总流量固定为 \(K\)，所以反过来考虑，「至少有 \(L\) 对 “A-A” 型的匹配」，则「至多有 \(K-L\) 对 “A-B” 型的匹配」。

考虑这样建图（以下「边权」指边的费用）：

  • \(a,b\) 两个序列各自作为二分图的一个部，\(a\) 部与源点 \(S\) 的边权为 \(a_i\)，\(b\) 部与汇点同理；
  • \(a_i\) 到 \(b_i\) 直接连边，表示一种 “A-A” 型的匹配；
  • 新建两个特殊点 \(p,q\)，边 \(p\to q\) 容量限制为 \(K-L\)，用于处理 “A-B” 型：
    • \(a_i\) 向 \(p\) 连边，\(q\) 向 \(b_j\) 连边；
    • 这样 \(a_i\to p\to q\to b_j\) 即构成了 “A-B” 型匹配。

流网络大概长这样：

直接限制总流量为 \(K\) 跑最大费用流，可以获得不错的部分分。

既然是费用流，而且流网络比较规整，可以尝试模拟费用流 —— 简单的说就是快速找“\(S\) 到 \(T\) 的最长路”。考虑一条最长路会长什么样。

一个点「被选」指它的匹配方式是 A-B 匹配，一个 S 部的被选点 \(u\) 具有反向边 \(p\to u\)，一个 T 部的被选点 \(v\) 具有反向边 \(v\to q\)。

一个点「为空」指它还没有被匹配。

一条路径开头一定是 \(S\to a\)，结尾一定是 \(b'\to T\)，其中 \(a,b'\) 均为空。大概会有以下四种情况：

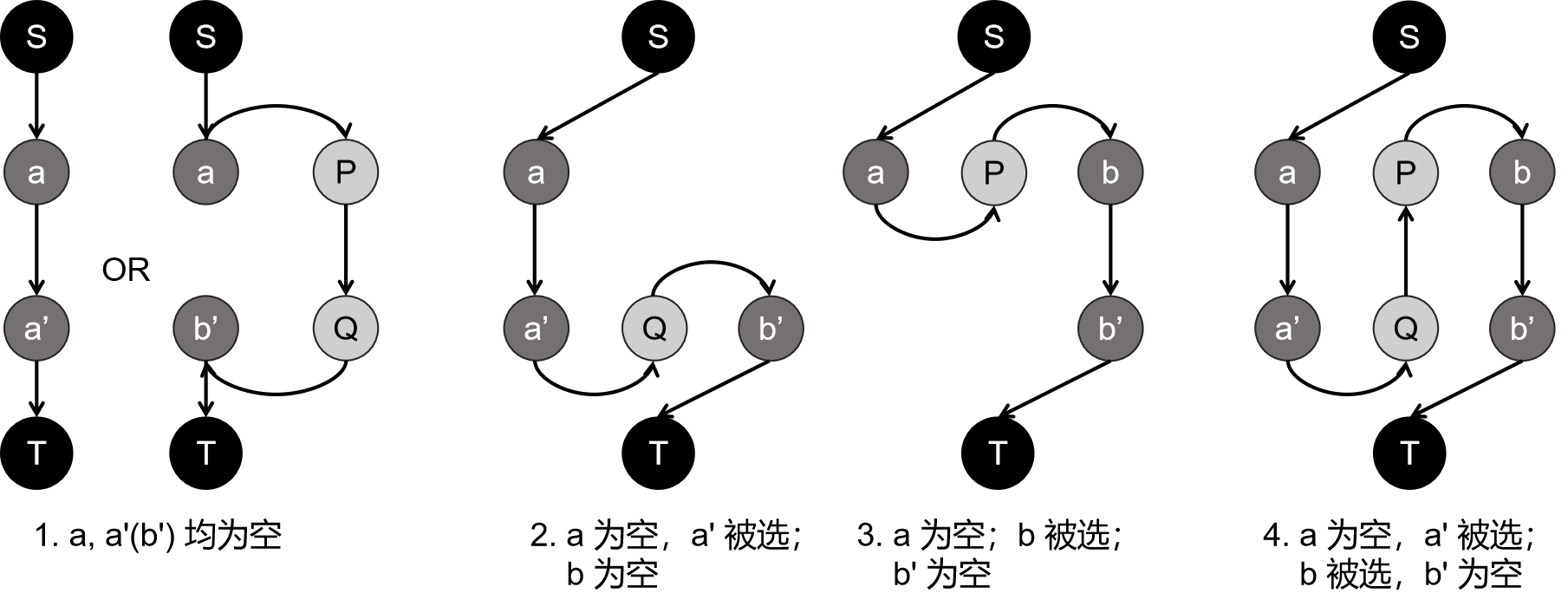
注意到只有 \(S\to a\) 和 \(b'\to T\) 这两种边有费用，所以决定路径长度的其实就只有开头和结尾。

于是我们发现我们需要维护以下信息：

  1. 空的 \(a\)；
  2. 空的 \(b'\)；
  3. \(a'\) 被选，且 \(a\) 为空的 \(a\)；
  4. \(b\) 被选，且 \(b'\) 为空的 \(b'\)；

这四类信息都可以用堆维护最大值。继续考虑如何模拟费用流——

我们每找一条最长路，就会把 \(S\to T\) 的总流量增加 \(1\)，所以限制总流量为 \(K\) 则只需要找 \(K\) 次最长路即可。

然后这张流网络上还有一条特殊的边 \(P\to Q\)，需要维护它的容量。在上图列出的四种情况中：

  1. 若为 \(a\to a'\)，则容量不变；若为 \(a\to b'\)，则容量 \(-1\)；
  2. 容量不变；
  3. 容量不变；
  4. 容量 \(+1\)。

另外，我们有时会发现 \(a\) 和 \(a'\) 同时被选，显然是不优的。这种时候就可以把 \(a\) 和 \(a'\) 同时改为不被选，答案不变但是 \(P\to Q\) 容量 \(+1\)。

直接模拟即可。

源代码

/*Lucky_Glass*/
#include <queue>
#include <cstdio>
#include <cstring>
#include <cassert>
#include <algorithm>

inline int rin(int &r) {
  int c = getchar(); r = 0;
  while ( c < '0' || '9' < c ) c = getchar();
  while ( '0' <= c && c <= '9' ) r = r * 10 + (c ^ '0'), c = getchar();
  return r;
}

typedef long long llong;
typedef std::pair<int, int> pii;

#define CON(typ) const typ &

const int N = 2e5 + 10;

int ncas, n, nk, nl;
int num[N << 1];
std::priority_queue<pii> emp[2], opp[2], par;
bool cov[N << 1], used[N << 1];

void clean() {
  while ( !emp[0].empty() ) emp[0].pop();
  while ( !emp[1].empty() ) emp[1].pop();
  while ( !opp[0].empty() ) opp[0].pop();
  while ( !opp[1].empty() ) opp[1].pop();
  while ( !par.empty() ) par.pop();
  for ( int i = 1; i <= (n << 1); ++i )
    cov[i] = used[i] = false; 
}
int empTop(CON(bool) typ) {
  while ( !emp[typ].empty() && used[emp[typ].top().second] ) emp[typ].pop();
  return emp[typ].empty() ? -1 : emp[typ].top().second;
}
int oppTop(CON(bool) typ) {
#define OPPID(x) ((x) <= n ? (x) + n : (x) - n)
  while ( !opp[typ].empty() && (used[opp[typ].top().second]
         || !cov[OPPID(opp[typ].top().second)]) )
    opp[typ].pop();
  return opp[typ].empty() ? -1 : opp[typ].top().second;
#undef OPPID
}
int parTop() {
  while ( !par.empty() && (used[par.top().second]
         || used[par.top().second + n]) )
    par.pop();
  return par.empty() ? -1 : par.top().second;
}
void checkCross(CON(int) id, int &rem) {
#define OPPID(x) ((x) <= n ? (x) + n : (x) - n)
  if ( cov[OPPID(id)] && cov[id] ) {
    cov[OPPID(id)] = cov[id] = false;
    ++rem;
  }
#undef OPPID
}
llong findPath(int &rem) {
#define GID(x) (std::make_pair(num[x], x))
  llong ee = -1, eo = -1, oe = -1, oo = -1;
  int etop[2] = {empTop(0), empTop(1)}, otop[2] = {oppTop(0), oppTop(1)},
      ptop = parTop();
  if ( rem && ~etop[0] && ~etop[1] ) ee = num[etop[0]] + num[etop[1]];
  if ( !rem && ~ptop ) ee = num[ptop] + num[ptop + n];
  if ( ~etop[0] && ~otop[1] ) eo = num[etop[0]] + num[otop[1]];
  if ( ~otop[0] && ~etop[1] ) oe = num[otop[0]] + num[etop[1]];
  if ( ~otop[0] && ~otop[1] ) oo = num[otop[0]] + num[otop[1]];
  llong mx = std::max(std::max(ee, eo), std::max(oe, oo));
  if ( mx == ee ) {
    if ( rem ) {
      --rem;
      used[etop[0]] = used[etop[1]] = true;
      cov[etop[0]] = cov[etop[1]] = true;
      checkCross(etop[0], rem), checkCross(etop[1], rem);
      opp[1].push(GID(etop[0] + n));
      opp[0].push(GID(etop[1] - n));
    }
    else {
      used[ptop] = used[ptop + n] = true;
    }
  } else if ( mx == eo ) {
    used[etop[0]] = used[otop[1]] = true;
    cov[etop[0]] = true, cov[otop[1] - n] = false;
    checkCross(etop[0], rem);
    opp[1].push(GID(etop[0] + n));
  } else if ( mx == oe ) {
    used[otop[0]] = used[etop[1]] = true;
    cov[etop[1]] = true, cov[otop[0] + n] = false;
    checkCross(etop[1], rem);
    opp[0].push(GID(etop[1] - n));
  } else {
    ++rem;
    used[otop[0]] = used[otop[1]] = true;
    cov[otop[0] + n] = cov[otop[1] - n] = false;
  }
  return mx;
}
void solve() {
  rin(n), rin(nk), rin(nl);
  clean();
  for ( int i = 1; i <= n; ++i )
    emp[0].push(std::make_pair(rin(num[i]), i));
  for ( int i = 1; i <= n; ++i ) {
    emp[1].push(std::make_pair(rin(num[i + n]), i + n));
    par.push(std::make_pair(num[i] + num[i + n], i));
  }
  llong ans = 0;
  int rem = nk - nl;
  for ( int i = 0; i < nk; ++i )
    ans += findPath(rem);
  printf("%lld\n", ans);
}
int main() {
  freopen("sequence.in", "r", stdin);
  freopen("sequence.out", "w", stdout);
  rin(ncas);
  while ( ncas-- ) solve();
  return 0;
}

THE END

Thanks for reading!

若写花开花落花飞花舞太遥远
若写风去风回风追风止太疲倦
若写日升月落斗转星移太幽怨
写你看我一颦一笑太腼腆

——《词不达意》 By 夏语遥

> Link 词不达意 - 网易云

posted @ 2021-06-10 08:52  Lucky_Glass  阅读(90)  评论(0)  编辑  收藏  举报
TOP BOTTOM