「SOL」E-Lite (Ural Championship 2013)
为什么这数据能水到可以枚举角度 ac 啊
# 题面
给你 \(n\) 个平面向量 \((x_i,y_i)\),对于每个 \(k=1\sim n\),求「从给出的 \(n\) 个向量中不重复地选择 \(k\) 个,\(k\) 个向量的和的模长最大是多少」。
数据规模:\(n\le1000\)。
# 解析
这种「选择 \(k\) 个」的题目,我们之前往往会从 DP 考虑,或者贪心求解。但是我们发现向量并不满足局部最优就是全局最优。
于是这道题我们换一个思路,不从选的过程考虑,而从选的结果 —— 也就是答案的角度考虑。
如果我们知道了答案为 \(\mathbf{v}\),那么一定是由在 \(\mathbf{v}\) 方向上投影最大的 \(k\) 个向量组成的。于是我们可以尝试「旋转」答案向量的方向,然后贪心地选取向量。
虽然数据水,离散地枚举答案向量角度可以 ac,但是角度毕竟是连续的,这种做法不是很靠谱(但是很难卡掉)。
连续的枚举一般考虑枚举临界点。不妨设我们逆时针旋转答案向量 \(\mathbf{v}\),记 id[i] 表示当前在 \(\mathbf{v}\) 方向上投影从大到小第 \(i\) 个向量是哪一个,同理定义 rnk[i] 表示 \(i\) 向量的排名(rnk[id[i]] = i)。
我们发现只有 id 发生变化 —— 也即两个向量的相对投影大小改变时,答案才会改变。设 \(\mathbf{u,v}\) 为两个方向不同的向量:
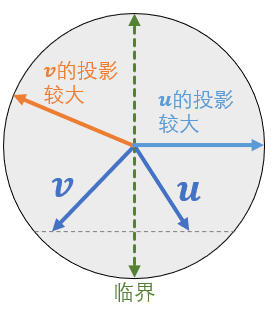
于是一对向量会产生两个临界点,总共会有 \(\mathcal{O}(n^2)\) 个临界。将它们极角排序过后逆时针扫一遍。
每经过一个临界点,就会有 rank 相邻的两个向量的 rank 发生交换(记为 rnk, rnk + 1)。扫描时,维护当前 rank,当 rnk, rnk + 1 交换时,只会改变前 rnk 个和前 rnk + 1 个向量的和,\(\mathcal{O}(1)\) 更新答案即可。
唯一的麻烦点是给出的 \(n\) 个向量可能重叠……我的处理是把重叠的向量看成一个,记录一下个数。只能自己意会一下或者看一看代码了。
# 源代码
/*Lucky_Glass*/
#include <cmath>
#include <cstdio>
#include <cstring>
#include <cassert>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long double ldouble;
const int N = 1005;
const ldouble EPS = 1e-12;
#define con(typ) const typ &
#define sec second
#define fir first
template<class typ> typ iAbs(con(typ) key) {return key < 0 ? -key : key;}
template<class typ> int sgn(con(typ) key) {
if ( iAbs(key) <= EPS ) return 0;
return key < 0 ? -1 : 1;
}
struct Vector {
ldouble x, y;
Vector() {}
Vector(con(ldouble) _x, con(ldouble) _y) : x(_x), y(_y) {}
ldouble len() const {return x * x + y * y;}
Vector operator - (con(Vector) p) const {
return Vector(x - p.x, y - p.y);
}
Vector operator + (con(Vector) p) const {
return Vector(x + p.x, y + p.y);
}
friend ldouble dot(con(Vector) p, con(Vector) q) {
return p.x * q.x + p.y * q.y;
}
Vector operator -() const {return Vector(-x, -y);}
bool operator != (con(Vector) p) const {
return sgn(x - p.x) || sgn(y - p.y);
}
bool operator < (con(Vector) p) const {
if ( sgn(x - p.x) ) return sgn(x - p.x) < 0;
return sgn(y - p.y) < 0;
}
Vector cwise90() const {return Vector(y, -x);}
} sum[N];
struct Data {
Vector v; int cnt;
Data() {}
Data(con(Vector) _v, con(int) _c) : v(_v), cnt(_c) {}
} dat[N];
int nn, n, ndv;
pair<int, int> inp[N];
int cnt[N], rnk[N];
ldouble ans[N];
struct Divi {
int a, b;
ldouble ang;
Divi() {}
Divi(con(int) _a, con(int) _b, con(ldouble) _ang)
: a(_a), b(_b), ang(_ang) {}
bool operator == (con(Divi) p) const {return !sgn(ang - p.ang);}
static bool cmpAng(con(Divi) p, con(Divi) q) {return sgn(p.ang - q.ang) < 0;}
static bool cmpID(con(Divi) p, con(Divi) q) {
if ( rnk[p.a] != rnk[q.a] ) return rnk[p.a] < rnk[q.a];
return rnk[p.b] < rnk[q.b];
}
} dv[N * N];
void init() {
sum[0] = Vector(0, 0);
for (int i = 1, tmp = 0; i <= n; i++) {
for (int j = 1; j <= dat[i].cnt; j++) {
tmp++;
sum[tmp] = sum[tmp - 1] + dat[i].v;
ans[tmp] = sum[tmp].len();
}
rnk[i] = i, cnt[i] = tmp;
}
}
// q is better than p then
void done(con(int) p, con(int) q) {
// assert( rnk[p] == rnk[q] - 1 );
int tmp = cnt[rnk[p] - 1];
for (int i = 1; i <= dat[q].cnt; i++) {
tmp++;
sum[tmp] = sum[tmp - 1] + dat[q].v;
ans[tmp] = max(ans[tmp], sum[tmp].len());
}
cnt[rnk[p]] = tmp;
for (int i = 1; i <= dat[p].cnt; i++) {
tmp++;
sum[tmp] = sum[tmp - 1] + dat[p].v;
ans[tmp] = max(ans[tmp], sum[tmp].len());
}
swap(rnk[p], rnk[q]);
}
int main() {
scanf("%d", &nn);
for (int i = 1; i <= nn; i++)
scanf("%d%d", &inp[i].fir, &inp[i].sec);
sort(inp + 1, inp + 1 + nn);
for (int i = 1; i <= nn;) {
int j = i;
while ( j <= nn && inp[i] == inp[j] ) j++;
dat[++n] = Data(Vector(inp[i].fir, inp[i].sec), j - i);
inp[n] = inp[i];
i = j;
}
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++) {
double k1 = atan2(inp[j].fir - inp[i].fir, inp[i].sec - inp[j].sec),
k2 = atan2(inp[i].fir - inp[j].fir, inp[j].sec - inp[i].sec);
dv[++ndv] = Divi(j, i, k1);
dv[++ndv] = Divi(i, j, k2);
}
sort(dv + 1, dv + 1 + ndv, Divi::cmpAng);
init();
for (int i = 1; i <= ndv; ) {
int j = i;
while ( j <= ndv && dv[i] == dv[j] ) j++;
sort(dv + i, dv + j, Divi::cmpID);
while ( i < j ) {
done(dv[i].a, dv[i].b);
i++;
}
}
for (int i = 1; i <= nn; i++)
printf("%.8f\n", (double)sqrt(ans[i]));
return 0;
}


