「NOTE」支配树

理性愉悦(×)在线自闭(√)（和析合树有得一拼）
感谢大神的博客：Meowww~（本文的证明思路同上博客）

# 概念

支配树是建立在单源有向图上的有根树。单源有向图又被称为“流程图”，其特点除了有向，还有存在一个源点使得源点可以到达任意一个点。

在流程图上定义支配关系，设源点为 \(r\)：如果 \(r\) 到 \(v\) 的每一条路径都经过了 \(u\)，则 \(u\) 支配 \(v\)。

非常显然的，对于 \(v\)（\(v\neq r\)）来说，有两个平凡的支配点 \(v,r\)，一般来说都不会考虑 \(v\) 本身作为 \(v\) 的支配点。但是我们知道，往往是其他不平凡的支配点比较重要。

定义1-最近支配点

对于一个点 \(v\)（\(v\neq r\)），如果 \(u\) 是 \(v\) 的一个支配点，并且任意一个 \(v\) 的支配点都支配 \(u\)，则称 \(u\) 为 \(v\) 的最近支配点；记作 \(\operatorname{idom}(v)=u\)。

定理一

对于点 \(v\)，存在唯一的 \(\operatorname{idom}(v)\)。

首先支配关系具有一定的“传递性”，即如果 \(a\) 支配 \(b\)、\(b\) 支配 \(c\) 则 \(a\) 支配 \(c\)。则可以证明：

推论1

如果 \(a\) 支配 \(c\)、\(b\) 支配 \(c\)，则 \(a\) 支配 \(b\) 或 \(b\) 支配 \(a\)。否则存在 \(r\) 经过 \(b\) 到达 \(v\) 的路径不经过 \(a\)，与 \(a\) 支配 \(c\) 矛盾。

那么有且仅有一个 \(v\) 的支配点支配 \(v\) 的所有支配点，即 \(\operatorname{idom}(v)\)。

那么将 \(\operatorname{idom}(v)\) 作为 \(v\) 的父亲，可以获得一棵有根树，称为支配树。

接下来会介绍 Lengauer-Tarjan 算法，在 \(O(n\log n)\) 时间复杂度内求出支配树，进而获得支配关系。

# 一些记号

先从流程图的源点出发DFS整张流程图，得到DFS树以及对应的DFS序。DFS树上有 4 种边：树边，前向边，后向边和横插边

png1

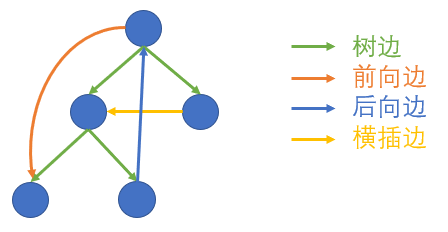
注意到横插边只会从右边的子树指向左边的子树，因此前向边和树边都是从低DFS序指向高DFS序，后向边和横插边就反过来。

\(u\to v\)，表示 \(u\) 到 \(v\) 的一条有向边；
\(u\leadsto v\)，表示存在 \(u\) 到 \(v\) 的一条路径；
\(u\overset .\to v\) 表示 \(u\) 到 \(v\) 的一条只经过树边的路径；
\(u\overset+\to v\) 表示 \(u\overset.\to v\) 且 \(u\neq v\)；
\(dfn_u\) 表示 \(u\) 的 DFS 序；
以下所有「点的大小比较」都是指 DFS 序进行比较。

# 理论证明

引理一（路径引理）

若 \(dfn_u\le dfn_v\) 则 \(u\) 到 \(v\) 的路径必经过 \(u,v\) 的公共祖先。

要么 \(v\) 是 \(u\) 的后继，要么 \(v\) 是 \(u\) 的更右边的子树中的点。

对于第一种情况，\(u\) 就是公共祖先，必须经过；
对于第二种情况，考虑删去 \(u,v\) 的 LCA 到 \(r\) 的所有点（也就是删去所有公共祖先），此时不可能通过树边从 \(u\) 的子树到达 \(v\) 的子树；
另外前向边、后向边都不跨子树，而横插边只从右边的子树指向左边的子树，于是不存在向右跨越子树的边，不可能到达。

由于并不好计算 \(\operatorname{idom}(u)\)，所以考虑引入一些定义来辅助计算——

定义2-半支配点

点 \(v\) 满足：存在路径 \(P=v\leadsto u\)，且 \(P\) 上除去 \(u,v\) 两点不存在 dfn 比 \(u\) 小的点。

满足上述条件的最小的点 \(v\) 称为 \(u\) 的半支配点，记作 \(\operatorname{sdom}(u)\)。

形式化的定义为：

\[\operatorname{sdom}(u)=\min\left\{v|\ \exists v\leadsto u=(v,a_1,a_2,\dots,a_m,u),a_i< u\right\} \]

注意到 \(\operatorname{sdom}(u)\) 并不一定是 \(u\) 的一个支配点，比如下图：

png2

\(v\) 是 \(u\) 的半支配点但是显然不支配 \(u\)。

但是 \(\operatorname{sdom}(u)\) 是有潜力成为支配点的点，在之后的证明中我们会看到任何一个点的 \(\operatorname{idom}(u)\) 要么是 \(\operatorname{sdom}(u)\)，要么是另一个点的 \(\operatorname{sdom}(v)\)。

而且我们发现 \(\operatorname{sdom}(u)\lt u\)（\(u\neq r\)），因为 \(fa(u)\) 一定是 \(u\) 的半支配点的「候选」。

引理二

对于任意 \(u\neq r\)，有 \(\operatorname{idom}(u)\overset+\to u\) 且 \(\operatorname{sdom}(u)\overset+\to u\)。

如果 \(\operatorname{idom}(u)\) 不是 \(u\) 的祖先，那么 \(r\) 就可以直接经过树边到达 \(u\)，就与 \(\operatorname{idom}(u)\) 支配 \(u\) 矛盾。

如果 \(\operatorname{sdom}(u)\) 不是 \(u\) 的祖先：

首先，\(\operatorname{sdom}(u)\) 不可能是右边的子树或者 \(u\) 的后继，因为 \(\operatorname{sdom}(u)<u\)，那么只能是左边的子树；
根据路径引理，从 dfn 小的点到大的点必然经过公共祖先，而 \(u\) 和 \(\operatorname{sdom}(u)\) 的公共祖先一定比 \(u\) 小，违背了 \(\operatorname{sdom}(u)\) 的定义。

引理三

对于任意 \(u\neq r\)，有 \(\operatorname{idom}(u)\overset.\to \operatorname{sdom}(u)\)。

考虑反证。根据引理二，\(\operatorname{sdom}(u)\) 和 \(\operatorname{idom}(u)\) 都是 \(u\) 的祖先。所以如果引理三不成立，则 \(\operatorname{sdom}(u)\overset+\to \operatorname{idom}(u)\)。

因为 \(\operatorname{sdom}(u)\) 可以不经过比 \(u\) 小的点到达 \(u\)，即可以不经过 \(\operatorname{idom}(u)\)，则存在 \(r\overset.\to \operatorname{sdom}(u)\leadsto u\) 不经过 \(\operatorname{idom}(u)\)，矛盾。

引理四

对于点 \(w\)，任意 \(v\overset.\to w\) 满足 \(v\overset.\to \operatorname{idom}(w)\) 或 \(\operatorname{idom}(w)\overset.\to \operatorname{idom}(v)\)。

由引理二，可以推得 \(\operatorname{idom}(w),\operatorname{idom}(v),w,v\) 是在 \(r\overset{.}{\to}w\) 上的。

仍然考虑反证。此时相反情况只有 \(\operatorname{idom(v)}\overset{+}{\to}\operatorname{idom}(w)\overset{.}{\to}v\overset{.}{\to}w\)，比如下面这样：

png3

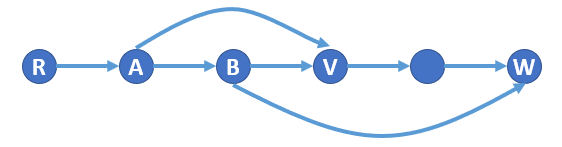
其中 \(A,B\) 分别为 \(\operatorname{idom}(v),\operatorname{idom}(w)\)，注意到 \(\operatorname{idom}(v)\neq\operatorname{idom}(w)\)，故必然存在 \(\operatorname{idom}(v)\leadsto v\) 不经过 \(\operatorname{idom}(w)\)。于是存在路径 \(r\overset{.}{\to}\operatorname{idom}(v)\leadsto v\overset{.}{\to}w\)，不经过 \(\operatorname{idom}(w)\)，矛盾。

完备的引理是对定理的铺垫~

定理二

对于 \(u\neq r\)，若所有满足 \(\operatorname{sdom}(u)\overset+\to v\overset.\to u\) 的点 \(v\) 都满足 \(\operatorname{sdom}(v)\ge \operatorname{sdom}(u)\)，则 \(\operatorname{idom}(u)=\operatorname{sdom}(u)\)。

这个定理就让 \(\operatorname{idom}(u)\) 和 \(\operatorname{sdom}(u)\) 有联系了~

由引理三，我们知道 \(\operatorname{idom}(u)\overset.\to \operatorname{sdom}(u)\)，则只需证明 \(\operatorname{sdom}(u)\) 支配 u。考虑反证，假设 \(\operatorname{sdom}(u)\) 不支配 u，则存在 \(r\leadsto u\) 不经过 \(\operatorname{sdom}(u)\)。

记该路径为 \(P=r\leadsto u\)。令 \(x\) 为 \(P\) 上最后一个 \(x\lt\operatorname{sdom}(u)\) 的点。

则 \(x\leadsto u\) 上一定存在点 \(y_0\) 满足 \(\operatorname{sdom}(u)\overset.\to y_0\overset+\to u\)（\(y_0\) 在 \(\operatorname{sdom}(u)\) 和 \(u\) 之间的链上），否则 \(x\) 就会成为 \(\operatorname{sdom}(u)\)。记所有满足条件的点 \(y_0\) 中最小的一个为 \(y\)。

若 \(y\neq \operatorname{sdom}(u)\)，由定理二得：\(\operatorname{sdom}(y)\ge \operatorname{sdom}(u)\)。

说明 \(P\) 上还有一个点 \(z\) 满足 \(z\lt y\)，否则 \(x\) 将成为 \(\operatorname{sdom}(y)\)。那么有 \(z\lt y\lt u\)，但是 \(y\) 是 \(P\) 上最小的 \(y\lt u\) 的点，产生矛盾。

则 \(y=\operatorname{sdom}(u)\)，因此 \(P\) 一定经过 \(\operatorname{sdom}(u)\)，即 \(\operatorname{sdom}(u)\) 支配 \(u\)。

定理三

对于 \(w\neq r\)，若存在 \(u_0\) 满足 \(\operatorname{sdom}(w)\overset+\to u_0\overset+\to w\) 使得 \(\operatorname{sdom}(u_0)\lt\operatorname{sdom}(w)\)；

记 \(\operatorname{sdom}(u_0)\) 最小的 \(u_0\) 为 \(u\)，则 \(\operatorname{idom}(u)=\operatorname{idom}(w)\)。

相当于是对定理二的补充。大概是这样一个图：

png4

考虑 \(\operatorname{idom}(u)\) 和 \(\operatorname{idom}(w)\) 的位置。

首先 \(\operatorname{idom}(w)\overset{.}{\to}\operatorname{sdom}(w)\) 且 \(\operatorname{idom}(u)\overset{.}{\to}\operatorname{sdom}(u)\)（引理三）；
由引理四，因为 \(u\overset{.}{\to}w\)，且不存在 \(u\overset{.}{\to}\operatorname{idom}(w)\)，所以只能是 \(\operatorname{idom}(w)\overset{.}{\to}\operatorname{idom}(u)\)。

于是整个情形如下图：

png5

只需要证明 \(\operatorname{idom}(u)\) 支配 \(w\)。考虑证明非平凡情况：\(\operatorname{idom}(u)\neq r\)。

任意取一条路径 \(P=r\leadsto w\)，令 \(P\) 中最后一个小于 \(\operatorname{idom}(u)\) 的点为 \(x\)。则存在 \(y_0\) 使得 \(\operatorname{idom}(u)\overset.\to y_0\overset+\to w\)，我们取最小的 \(y_0\) 作为 \(y\)。

因为 \(y\) 是满足条件的最小点，所以不存在 \(v\) 使得 \(\operatorname{idom}(u)\overset.\to v\overset+\to y\)。于是 \(x\) 是 \(\operatorname{sdom}(y)\) 的「候选」，\(\operatorname{sdom}(y)\le x\lt\operatorname{idom}(u)\le\operatorname{sdom}(w)\)。

若 \(\operatorname{sdom}(w)\overset{+}{\to}y\overset{+}{\to}w\)，则 \(y\) 可以作为定理中的 \(u_0\)，而 \(\operatorname{sdom}(y)\le x\lt\operatorname{sdom}(u)\)，与 \(u\) 是 \(\operatorname{sdom}(u_0)\) 最小的 \(u_0\) 矛盾。

因此 \(\operatorname{idom}(u)\overset{.}{\to}y\overset{.}{\to}\operatorname{sdom}(w)\)。

此时，如果 \(y\neq\operatorname{idom}(u)\)，则存在 \(r\overset{.}{\to}x\leadsto y\overset{.}{\to}u\) 不经过 \(\operatorname{idom}(u)\)，矛盾。故 \(y=\operatorname{idom}(u)\)。

因此任意路径 \(P\) 都经过 \(\operatorname{idom}(u)\)，即 \(\operatorname{idom}(u)\) 支配 \(w\)。

得证，\(\operatorname{idom}(u)=\operatorname{idom}(w)\)。

推论2

对于 \(w\neq r\)，令 \(u\) 为 \(\operatorname{sdom}(w)\overset+\to u\overset.\to w\) 中 \(\operatorname{sdom}(u)\) 最小的，则有：

\[\operatorname{idom}(w)=\begin{cases}\operatorname{sdom}(w)&\operatorname{sdom}(u)\ge \operatorname{sdom}(w)\\\operatorname{idom}(u)&\operatorname{sdom}(u)< \operatorname{sdom}(w)\end{cases} \]

其实就是定理二三的综合。

最后只剩下如何求 \(\operatorname{sdom}(w)\)。

定理四

对于 \(w\neq r\)，\(\operatorname{sdom}(w)\) 只可能是下面两种情况

存在边 \(v\to w\)，\(\operatorname{sdom}(w)=v\)；
点 \(u\) 满足 \(u\overset{.}{\to}v\to w\)，其中 \(v\gt w\)，\(\operatorname{sdom}(w)=\operatorname{sdom}(u)\)。

形式化地：

\[\operatorname{sdom}(w)=\min\{\{v|(v,w)\in E\}\cup\{\operatorname{sdom}(u)|u>w,\exists(v,w)\in E,u\overset.\to v\}\} \]

显然两种情况都满足了 \(\operatorname{sdom}(w)\) 的定义，只要证明 \(\operatorname{sdom}(w)\) 一定符合两种情况之一：

\(\operatorname{sdom}(w)\leadsto w\) 只有一条边，对应第一个种情况；
\(\operatorname{sdom}(w)\leadsto w\) 大于一条边，对应第二种情况，记第二种情况中 \(\operatorname{sdom}(u)\) 的最小值为 \(k\)；则 \(\operatorname{sdom}(w)\le k\)。
记 \(P=\operatorname{sdom}(w)\leadsto w\) 上 \(\operatorname{sdom}(w)\) 以外的最小的点为 \(y\)。那么 \(\operatorname{sdom}(w)\leadsto y\) 上除去 \(\operatorname{sdom}(w), y\) 的所有点都大于 \(y\)，也即 \(\operatorname{sdom}(w)\) 是 \(\operatorname{sdom}(y)\) 的「候选」。
根据描述，\(y\) 符合第二种情况中 \(u\) 的定义，则 \(k\le\operatorname{sdom}(y)\)。
而 \(\operatorname{sdom}(y)\le\operatorname{sdom}(w)\)，所以 \(k\le\operatorname{sdom}(w)\)。
综上 \(\operatorname{sdom}(w)=k\)。

得证。

# Lengauer-Tarjan

有了上述定理作为基础，Lengauer-Tarjan算法就被设计出来，以 \(O(n\log n)\) 的复杂度计算 \(\operatorname{idom}(u),\operatorname{sdom}(u)\)。

算法流程大概如下：

先DFS一遍，求一个DFS树，然后初始化 \(\operatorname{sdom}(u)=u\)（为了方便……）；
根据定理四，按dfn从大到小枚举 \(w\)，计算 \(\operatorname{sdom}(w)\)（在每次计算前，\(\gt w\) 的 \(\operatorname{sdom}()\) 已经计算好了）：
枚举连向 \(w\) 的点 \(u\)，计算 \(u\) 沿着 \(fa(u)\) 往上爬到第一个dfn小于 \(w\) 的点，这条路径上最小的 \(\operatorname{sdom}()\)。
当然我们不会直接枚举 \(fa(u)\) 向上跳，需要用带权并查集维护有根树结构——每次计算完 \(\operatorname{sdom}(w)\)，就把 \(w\) 在并查集中连向 \(fa(w)\)，并查集用路径压缩，压缩时更新路径上最小的 \(\operatorname{sdom}(u)\) 对应的 \(u\)（详见代码）。
当我们计算完 \(\operatorname{sdom}(w)\) 时，在并查集上 \(w\) 的子树上所有点一定都连向了 \(fa(w)\)，因此可以枚举 \(\operatorname{sdom}(u)\) 为 \(fa(w)\) 的点 \(u\)，根据推论2，用带权并查集求出 \(u\) 到 \(\operatorname{sdom}(u)\) 的路径上最小的 \(\operatorname{sdom}(v)\) 对应的 \(v\)，若 \(\operatorname{sdom}(v)<\operatorname{sdom}(u)\)，则给 \(\operatorname{idom}(u)\) 打上“\(v\) 的标记”，表示 \(\operatorname{idom}(u)=\operatorname{idom}(v)\)，否则直接 \(\operatorname{idom}(u)=\operatorname{sdom}(u)\)。
最后再扫一遍 \(\operatorname{idom}(u)\)，把有标记 \(v\) 的 \(\operatorname{idom}(u)\) 的值赋值为 \(\operatorname{idom}(v)\)。

Hint. 因为我们时常要取一个点的dfn做大小比较，写代码的时候注意变量到底代表的是dfn还是一个点本身。

# 源代码

> 洛谷 P5180

对应题目P5180【模板】支配树

/*Lucky_Glass*/
#include <queue>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 2e5 + 10, M = 3e5 + 10;
#define con(typ) const typ &

struct Graph {
	int head[N], to[M], nxt[M], ncnt;
	void addEdge(con(int) u, con(int) v) {
		int p = ++ncnt;
		to[p] = v, nxt[p] = head[u];
		head[u] = p;
	}
	inline int operator [] (con(int) u) {return head[u];}
} gr, rg, bin;


int n, m, ndfn;
int dfn[N], idfn[N], sdom[N], idom[N], fa[N], ans[N], deg[N];

struct Dsu {
	int fa[N], val[N];
	void init(con(int) siz) {for (int i = 1; i <= siz; i++) val[i] = fa[i] = i;}
	int findF(con(int) u) {
		if ( u == fa[u] ) return u;
		int ret = findF(fa[u]);
		if ( sdom[val[fa[u]]] < sdom[val[u]] ) val[u] = val[fa[u]];
		return fa[u] = ret;
	}
	bool combine(int u, int v) {
		u = findF(u), v = findF(v);
		if ( u == v ) return false;
		fa[u] = v;
		return true;
	}
	int getVal(con(int) u) {findF(u); return val[u];}
} dsu;

inline int rin(int &r) {
	int b = 1, c = getchar(); r = 0;
	while ( c < '0' || '9' < c ) b = c == '-' ? -1 : b, c = getchar();
	while ( '0' <= c && c <= '9' ) r = (r * 10) + (c ^ '0'), c = getchar();
	return r *= b;
}
void dfs(con(int) u) {
	idfn[sdom[u] = dfn[u] = ++ndfn] = u;
	for (int it = gr[u]; it; it = gr.nxt[it])
		if ( !dfn[gr.to[it]] )
			fa[gr.to[it]] = u, dfs(gr.to[it]);
}
int main() {
	rin(n), rin(m);
	for (int i = 1, u, v; i <= m; i++) {
		rin(u), rin(v);
		gr.addEdge(u, v), rg.addEdge(v, u);
	}
	dfs(1);
	dsu.init(n);
	for (int i = ndfn; i >= 2; i--) {
		int u = idfn[i];
		for (int it = rg[u]; it; it = rg.nxt[it])
			if ( dfn[rg.to[it]] )
				sdom[u] = min(sdom[u], sdom[dsu.getVal(rg.to[it])]);
		bin.addEdge(idfn[sdom[u]], u);
		dsu.combine(u, fa[u]);
		for (int it = bin[fa[u]]; it; it = bin.nxt[it]) {
			int w = bin.to[it], uu = dsu.getVal(w);
			if ( sdom[uu] == sdom[w] ) idom[w] = idfn[sdom[w]];
			else idom[w] = -uu; // tag
		}
		bin.head[fa[u]] = 0;
	}
	queue<int> que;
	for (int i = 2; i <= ndfn; i++) {
		int u = idfn[i];
		if ( idom[u] < 0 ) idom[u] = idom[-idom[u]];
//		printf("%d : %d\n", u, idom[u]);
		deg[idom[u]]++;
	}
	for (int i = 1; i <= ndfn; i++)
		if ( !deg[idfn[i]] )
			que.push(idfn[i]);
	while ( !que.empty() ) {
		int u = que.front(); que.pop();
		ans[u]++;
		if ( u != 1 ) {
			ans[idom[u]] += ans[u];
			if ( !(--deg[idom[u]]) ) que.push(idom[u]);
		}
	}
	for (int i = 1; i <= n; i++)
		printf("%d%c", ans[i], i == n ? '\n' : ' ');
	return 0;
}

THE END

Thanks for reading!

只要极致谁比我放肆
展开双翅去奔跑像个孩子
写下你的名字在风中化成诗
再说一次不在乎方式
哪怕重新开始那也要坚持
别去拔你的刺那是你最美丽的旗帜

——《奔赴》By 司南

> Linked 奔赴-网易云

posted @ 2021-04-17 12:54 Lucky_Glass 阅读(190) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Lumen's Code Space

玻璃破碎的时候才会显现出它真正的棱角