「NOTE」概率生成函数
本质是生成函数,只是太特殊了就被单独「dia」了出来
# 概率生成函数
顾名思义,是概率的生成函数。具体地说,对于离散随机变量 \(X\),记 \(X=i\) 的概率为 \(f_i\),则记
这个生成函数有一些优美的性质……
- 若 \(i\) 能取到 \(X\) 的可能情况的全集(之后有一些题会看到「生成函数不代表全集」的情况),则 \(F(1)=1\);
- 根据期望的定义,\(E(X)=F'(1)\)(\(F(x)\) 对 \(x\) 求导)。
于是它被单独拿出来当成一个模型。下面将按照集训队论文的思路梳理概率生成函数的技巧。
#『例一』歌唱王国
经典老题
> Link BZOJ 1152
- 题面
给定一个长度为 \(n\) 的整数序列 \(T\),其中元素的范围在 \([1,m]\)。有一个初始为空的序列 \(S\)。
每次操作在 \([1,m]\) 的整数中等概率生成一个数加入 \(S\) 的末尾。若 \(S\) 中已经存在一个与 \(T\) 相同的子串,则结束操作,否则继续。
求期望操作多少次结束。
数据规模:\(n,m\le10^5\)。
- 解析
生成函数一般就是「题目要求什么就设什么的生成函数」,但是概率生成函数略微不同,因为它和期望的联系非常紧密(上文提到的第二条性质),所以要求期望,往往设的是概率的生成函数。
于是设 \(f_i\) 表示进行 \(i\) 次操作刚好结束的概率,记 \(F(x)\) 是 \(f_i\) 的生成函数。
首先操作一定会「结束」(在无穷远处结束也是「结束」),所以 \(F(x)\) 代表的所有状态是可能状态的全集。那么 \(F(1)=1\)。
我们的目标就是求得 \(E(X)=F'(1)\)。
然后考虑如何求 \(F'(1)\),需要构造辅助生成函数(不一定是概率生成函数,但例一是概率生成函数)。设 \(g_i\) 表示进行了 \(i\) 次操作还没有结束的概率(互补),\(G(x)\) 为其生成函数。
性质1
$$ G(x)x+1=F(x)+G(x) $$
考虑从一个未结束的状态(\(G(x)\))开始,进行一步操作,即 “\(G(x)x\)”,那么得到的状态可能是结束的状态也可能是未结束的状态——并且能够包含其中的几乎所有状态,即 “\(F(x)+G(x)\)”。
但是还遗漏了一个情况:\(G(x)\) 中包含的「初始状态」(没有进行任何操作)是无法用 \(G(x)x\) 来代表的,于是加 \(1\) 补充。或者你也可以理解为“补充常数项”。
性质2
$$ G(x)\left(\frac{x}{m}\right)^n=\sum_{i=1}^nF(x)\left(\frac{x}{m}\right)^{n-i}\big[T[1,j]=T[n-j+1,n]\big] $$
其中 $T[l,r]$ 表示 $T$ 从 $l$ 开始到 $r$ 结束的子串。
考虑从一个未结束的状态开始,直接在它后面加上整个 \(T\) 串。那么这个状态一定结束了,但是不是「恰好结束」。
可能整个串还没有加完的时候,当前串的末尾已经是 \(T\) 了。如下图:
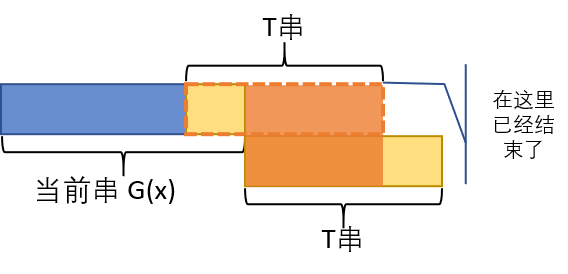
这意味着什么?注意上图标出的橙色段,同时是 \(T\) 的前缀和后缀——即 \(T\) 的 border,对应式子中的“\(\big[T[1,j]=T[n-j+1,n]\big]\)”。
而且在这种情况下,直接在当前串后面加上 \(T\),比对应的结束状态多加了 \(n-i\) 个字符,所以要补上 \(\left(\frac{x}{m}\right)^{n-i}\)。
这也就是「性质2」的含义。
有了这两个性质,我们尝试求 \(F'(1)\)。「性质1」的式子简单一些,考虑给它求导并代入 \(x=1\):
\(F'(1)=G(1)\),令人欣喜的结论。
简记 \(h_i=\big[T[1,i]=T[n-i+1,n]\big]\)。利用「性质2」求解,先化简:
再代入 \(x=1\):
还记得一开始我们找到的性质吗?\(F(1)=1\)——
于是就只需要判断 border,随便用 hash 判一判就好了。
# 源代码
点击展开/折叠代码
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
inline int rin(int &r){
int b=1,c=getchar();r=0;
while(c<'0' || '9'<c) b=c=='-'?-1:b,c=getchar();
while('0'<=c && c<='9') r=(r<<1)+(r<<3)+(c^'0'),c=getchar();
return r*=b;
}
const int N=1e5+10,MOD=1e4,P1=100000073,P2=300023,BAS2=300000047;
typedef unsigned long long ullong;
#define con(type) const type &
inline int hmul(con(int)a,con(int)b){return int(1ll*a*b%BAS2);}
inline int hadd(con(int)a,con(int)b){return a+b>=BAS2?a+b-BAS2:a+b;}
inline int hsub(con(int)a,con(int)b){return a-b<0?a-b+BAS2:a-b;}
ullong powp1[N];
int powp2[N];
struct Hash{
ullong p1;int p2;
Hash(){}
Hash(con(ullong)_p1,con(int)_p2):p1(_p1),p2(_p2){}
Hash operator -(con(Hash)b)const{return Hash(p1-b.p1,hsub(p2,b.p2));}
Hash operator +(con(int)d)const{return Hash(p1+d,hadd(p2,d));}
bool operator ==(con(Hash)b)const{return p1==b.p1 && p2==b.p2;}
Hash operator <<(con(int)d)const{return Hash(p1*powp1[d],hmul(p2,powp2[d]));}
}phas[N];
int n,len,cas;
int num[N];
void init(){
powp1[0]=powp2[0]=1;
for(int i=1;i<N;i++) powp1[i]=powp1[i-1]*P1;
for(int i=1;i<N;i++) powp2[i]=hmul(powp2[i-1],P2);
}
Hash subhash(con(int)le,con(int)ri){
return phas[ri]-(phas[le-1]<<(ri-le+1));
}
int main(){
init();
rin(n),rin(cas);
while(cas--){
rin(len);
for(int i=1;i<=len;i++){
rin(num[i]);
phas[i]=(phas[i-1]<<1)+num[i];
}
int tmp=n%MOD,ans=0;
for(int i=1;i<=len;i++,tmp=tmp*n%MOD)
if(subhash(1,i)==subhash(len-i+1,len)){
ans+=tmp;
if(ans>=MOD) ans-=MOD;
}
printf("%04d\n",ans);
}
return 0;
}
# 『例二』多串匹配问题
- 题面
一个随机数生成器,生成数 \(i\) 的概率为 \(p_i\),数的范围在 \([1,m]\)。给定 \(n\) 个串,第 \(i\) 个串 \(T_i\) 长度为 \(L_i\)。
初始有一个空序列,每次用随机数生成器生成一个数加在序列的末尾。当给定的 \(n\) 个串每一个都出现在了序列中(是序列的子串),就停止操作。
问最后序列的期望长度。
数据规模:\(n\le15,m\le10^5,L_i\le20000\)。
- 解析
实际上和『例一』大同小异。首先,所有串都出现并不容易限制。设第 \(i\) 个串第一次出现的时间为 \(t_i\),原问题是让我们求 \(t_i\) 的最大值的期望,可以 Min-Max 反演,转化为求「第一次出现集合 \(S\) 中的某一个串的时间」的期望。
按照一般套路,设 \(f_i\) 表示最终序列长度为 \(i\) 的概率,\(F(x)\) 为其生成函数。由于这道题有多串,特别地,我们设 \(F_i(x)\) 表示「序列因为第一次出现串 \(i\) 而结束」的概率生成函数。
类似『例一』我们仍然互补地设辅助生成函数 \(G(x)\):\(g_i\) 表示序列长度为 \(i\) 时还未结束的概率。
仍然有在一个未结束的状态的基础上再进行一次操作,会得到一个结束状态或一个非结束状态:
然后考虑在未结束状态的末尾加上整个 \(i\) 串,一定会是一个结束状态。和『例一』一样,仍然可能在 \(i\) 串整个加完之前就已经结束了,不同的是可能不是因为出现了串 \(i\) 而结束。
不妨枚举已经加入了 \(j\) 个字符,就已经出现了串 \(k\)。
简记一些记号:
- \(h(i,j,k)=[T_i[1,j]=T_k[L_k-j+1,L_k]\);
- \(P(T_i)=\prod\limits_{w=1}^{L_i}p_{T_{iw}}\);
- \(P(T_i[l,r])=\prod\limits_{w=l}^rp_{T_{iw}}\)。
所有 \(n\) 个字符串都可以写出上面这个式子:
分析了这么多,回过头来看我们要求什么——\(F'(1)\)。
对式 \(\eqref{2.1}\) 两边求导并代入 \(x=1\):
于是我们需要求 \(G(1)\),唯一相关的式子是 \(n\) 个式子 \(\eqref{2.2}\)。
再对 \(\eqref{2.2}\) 代入 \(x=1\):
我们可以把上式看成关于 \(G(1)\) 和 \(F_k(1)\) 的方程,也就是说我们有 \(n+1\) 个未知数但是只有 \(n\) 个方程??
实际上还有一个方程:
这样方程就够了,可以高斯消元解出 \(G(1)\)。
# 「传统题」小结
『例一』『例二』都是较为模板,且推导较为单一的经典题。其共同点是
- 题目要求某离散随机变量 \(X\) 的期望,则设出对应 \(X=i\) 的概率 \(p_i\) 的生成函数;
- 设置辅助生成函数则考虑“互补型”,即原题要求「已经结束」则设「还未结束」。
其中第一点是概率生成函数的通法,但是第二点并不是所有题都适用的。
下面来看一下不那么“传统”的题,然后你就知道为什么第二点并不是通法了
# 『例三』开关
题解参见下链接。
> Link 「SOL」开关
假如仍然设置互补型辅助函数,即「按了 \(i\) 次还未开门」,显然完全无法简化问题——原因是无法找到 \(F(x)\) 和 \(G(x)\) 的关系。
(可能会继续更,希望不会咕)


