「SOL」战争(JSOI 洛谷)
一道融合了好多计算几何技巧的题目
# 题面
> Linked 洛谷 P4557
给定两组散点 \(A,B\),给定 \(Q\) 组询问,每次询问给出向量 \(v=(dx,dy)\):
求将 \(B\) 的散点全部移动 \(v\),得到新的散点集 \(B'\),是否存在 \(A\) 中的三个点构成的三角形与 \(B\) 中的三点构成的三角形有公共点。
\(|A|,|B|\le 10^5\),\(Q\le10^5\)。
# 解析
“存在 \(A\) 中三点和 \(B\) 中三点,使得构成的三角形有公共点”,等价于 \(A\) 构成的凸包与 \(B\) 构成的凸包有公共点。因为凸包包含散点集中的任意一个点,也就包含散点集中任意三个点构成的三角形。
于是第一步非常自然的,分别求出 \(A,B\) 的凸包,Andrew或者Graham随便,但是用Andrew比较好的是可以删掉凸包边上的点。
Hint.
那么在下面的解析中,默认 “$A,B$” 指的是散点集求得的凸包。
怎么判断凸包有没有交?如果时间复杂度比较宽松,就可以检测 \(A\) 的每个顶点,看是否在 \(B\) 里面,再检测 \(B\) 的顶点是否在 \(A\) 里面,这样最优复杂度也只能是 \(O(n\log n)\) 一次。显然不可过。
于是就要用到一个黑科技,叫做闽可夫斯基和(Minkowski);两个凸包 \(A,B\) 的闽可夫斯基和定义如下:
可以感受到它的几何意义就是“把凸包 \(B\) 沿着凸包 \(A\) 的边缘平移一圈得到的封闭图形”,那么显然这个封闭图形仍然是个凸包。举个简单的例子,将下图的黑色凸包和绿色凸包做闵可夫斯基和就可以得到橙色凸包:

这个有什么用?这是将两个凸包“相加”,能不能两个凸包“相减”?
我们把 \(B\) 以原点为对称中心对称得到 \(B^-\),那么我们对 \(A\) 和 \(B^-\) 做闵可夫斯基和就是:
因为 \(A,B^-\) 都是凸包,所以 \(C\) 也是凸包。而 \(C\) 就非常有用了,如果原点包含在 \(\mathbf C\) 中,那么 \(A,B\) 就有交点。
于是第二步就是要对 \(A,B^-\) 求闵可夫斯基和得到 \(C\)。
怎么求闵可夫斯基和?我们只需要找到 \(C\) 的边界,具体步骤如下:
- 分别找到 \(A,B\) 的最左下角的点 \(p,q\)(\(y\) 坐标最小的前提下 \(x\) 坐标最小);
- \(C\) 的第一个点 \(w=p+q\);
- 逆时针找凸包上与 \(p,q\) 相邻的边 \(\overrightarrow{E_p},\overrightarrow{E_q}\);
- 比较 \(E_p,E_q\) 的极角,找到靠右的一条边,比如说是 \(\overrightarrow{E_p}\);
- \(w\) 移动到 \(w+\overrightarrow E_p\);
- \(p\) 逆时针移动到下一个点;
这样 \(p,q\) 一直移动就会将 \(A,B\) 的每个点都遍历到,然后每次得到的 \(w\) 都是 \(C\) 边界上的点,特殊处理一下可以得到 \(C\) 的顶点,具体可以看代码。
Hint.
下面简记“凸包 $A$ 的每个点移动向量 $v$”得到的图形为 $A+v$。
以及对于两点 $p,q$,记 $p\pm q=(x_p\pm x_q,y_p\pm y_q)$
再看一下题目的要求,即 \(A\) 和 \(B+v\) 没有交;根据闽可夫斯基和就是判断
也就是判断 \((O+v)\) 这个点在不在凸包 \(C\) 内了。
最后一步,对 \(C\) 进行极角排序,如下图:
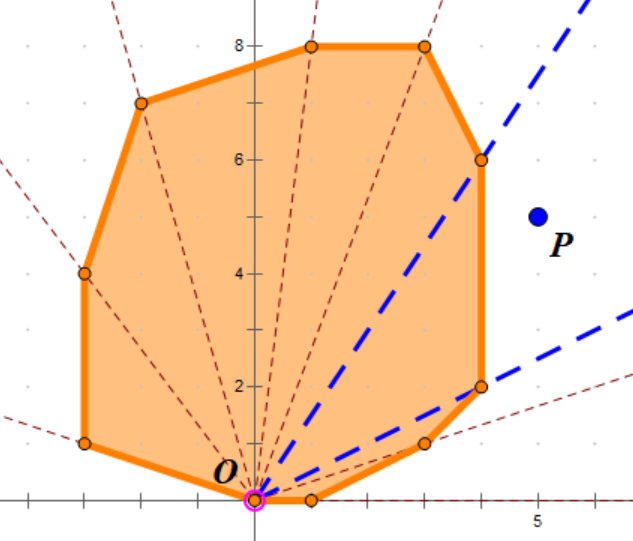
仍然是找到 \(C\) 的左下角的点 \(O\),然后向凸包的其他点引出射线。二分找到 \((O+v)\) 所在的位置(位于哪两条射线之间),然后用叉积判断一下点在线段的哪一侧即可。
# 源代码
/*Lucky_Glass*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<cassert>
#include<algorithm>
using namespace std;
namespace GEO{
typedef long long llong;
const double EPS=1e-15;
inline llong square(const int &key){return 1ll*key*key;}
inline int sgn(const llong &key){
if(!key) return 0;
return key<0? -1:1;
}
inline int sgn(const int &key){
if(!key) return 0;
return key<0? -1:1;
}
inline int sgn(const double &key){
if(fabs(key)<EPS) return 0;
return key<0? -1:1;
}
struct Vector{
int x,y;
Vector(int _x=0,int _y=0):x(_x),y(_y){}
friend double angle(const Vector &u,const Vector &v){
return acos(double((long double)dot(u,v)/(long double)u.len()/(long double)v.len()));
}
friend llong dot(const Vector &u,const Vector &v){return 1ll*u.x*v.x+1ll*u.y*v.y;}
friend llong cross(const Vector &u,const Vector &v){return 1ll*u.x*v.y-1ll*u.y*v.x;}
double len()const{return sqrt(square(x)+square(y));}
};
struct Point{
int x,y;
Point(int _x=0,int _y=0):x(_x),y(_y){}
Vector operator -(const Point &v)const{return Vector(x-v.x,y-v.y);}
Point operator +(const Vector &v)const{return Point(x+v.x,y+v.y);}
friend llong distPoint2(const Point &u,const Point &v){return square(u.x-v.x)+square(u.y-v.y);}
};
struct Line{
Point p;Vector d;
Line(){}
Line(Point _p,Vector _d):p(_p),d(_d){}
Line(Point s,Point t):p(s),d(t-s){}
};
//1=left / 0=on / -1=right
int fixSide(const Point &s,const Point &t,const Point now){
return sgn(cross(t-s,now-s));
}
bool cmpPointToX(const Point &u,const Point &v){
return sgn(u.x-v.x)? sgn(u.x-v.x)<0:sgn(u.y-v.y)<0;
}
bool cmpPointToY(const Point &u,const Point &v){
return sgn(u.y-v.y)? sgn(u.y-v.y)<0:sgn(u.x-v.x)<0;
}
void buildConvex(Point *org,int n,Point *res,int &nres){
nres=0;
sort(org,org+n,cmpPointToX);
for(int i=0;i<n;i++){
while(nres>1 && fixSide(res[nres-2],res[nres-1],org[i])<=0) nres--;
res[nres++]=org[i];
}
int tmp=nres;
for(int i=n-2;~i;i--){
while(nres>tmp && fixSide(res[nres-2],res[nres-1],org[i])<=0) nres--;
res[nres++]=org[i];
}
nres--;
}
void modelizeConvex(Point *org,int n){
int it=0;
for(int i=1;i<n;i++)
if(cmpPointToY(org[i],org[it]))
it=i;
rotate(org,org+it,org+n);
}
void Minkowski(Point *pa,int na,Point *pb,int nb,Point *res,int &nres){
//把凸包的左下角固定为凸包的第一个元素
modelizeConvex(pa,na),modelizeConvex(pb,nb);
pa[na]=pa[0],pb[nb]=pb[0];
int ma=0,mb=0;nres=0;
Point now=Point(pa[0].x+pb[0].x,pa[0].y+pb[0].y);
res[nres++]=now;
while(ma<na && mb<nb){
int re=sgn(cross(pa[ma+1]-pa[ma],pb[mb+1]-pb[mb]));
//如果两条边极角相同,则一起平移
//这样可以使得到的点都是凸包的顶点
if(!re) now=now+(pa[ma+1]-pa[ma])+(pb[mb+1]-pb[mb]),ma++,mb++;
else if(re>0) now=now+(pa[ma+1]-pa[ma]),ma++;
else now=now+(pb[mb+1]-pb[mb]),mb++;
res[nres++]=now;
}
while(ma<na){
now=now+(pa[ma+1]-pa[ma]),ma++;
res[nres++]=now;
}
while(mb<nb){
now=now+(pb[mb+1]-pb[mb]),mb++;
res[nres++]=now;
}
nres--;
}
}
using namespace GEO;
const int N=1e5+10;
int nA,nB,nply,cas,mA,mB;
Point ply[N<<1],covA[N<<1],covB[N];
bool ifFarthar(const Point &u,const Point &v){
return distPoint2(ply[0],u)<distPoint2(ply[0],v);
}
bool ifOutside(const Point &it){
//有可能点不位于射线之间,先特判掉
if(fixSide(ply[0],ply[1],it)<0 || fixSide(ply[0],ply[nply-1],it)>0) return true;
if(fixSide(ply[0],ply[1],it)==0) return ifFarthar(ply[1],it);
if(fixSide(ply[0],ply[nply-1],it)==0) return ifFarthar(ply[nply-1],it);
Vector vit=it-ply[0];
int lef=1,rig=nply-1;
while(lef+1<rig){
//用叉积判断点在射线哪边
int mid=(lef+rig)>>1,re=sgn(cross(ply[mid]-ply[0],vit));
//点在射线上
if(!re) return ifFarthar(ply[mid],it);
if(re<0) rig=mid;
else lef=mid;
}
//判断点在线段哪一侧
int re=sgn(cross(ply[lef]-it,ply[rig]-it));
return re<0;
}
int main(){
// freopen("input.in","r",stdin);
scanf("%d%d%d",&nA,&nB,&cas);
for(int i=0;i<nA;i++) scanf("%d%d",&ply[i].x,&ply[i].y);
//先对 A,B 求凸包
buildConvex(ply,nA,covA,mA);
for(int i=0;i<nB;i++){
scanf("%d%d",&ply[i].x,&ply[i].y);
ply[i].x*=-1,ply[i].y*=-1;
}
buildConvex(ply,nB,covB,mB);
//求出闵可夫斯基和
Minkowski(covA,mA,covB,mB,ply,nply);
for(int t=1;t<=cas;t++){
Point mov;scanf("%d%d",&mov.x,&mov.y);
//判断点是否在凸包内
printf("%d\n",!ifOutside(mov));
}
return 0;
}
THE END
Thanks for reading!
> Linked 余命3日少女-网易云


