学习笔记 - Ford-Fulkerson & EK
Ford-Fulkerson & EK - 学习笔记
之前网络流什么的快忘完了
老师讲课的时候一脸懵逼……开始系统复习,从最大流开始
标签:网络流-最大流
『预备』
首先复习了网络流的概念——
网络流是一个有向图,每一条边有一个流量限制(也可以叫做边权),图上有且仅有两个特殊点:源点-入度为0、汇点-出度为0。除此之外的所有点都有出度和入度。
网络流类似于“水流”,源点就相当于“无穷的水源”,从源点出发向其相邻边“流水”,边上“水”的流量不能超过其流量限制(容量限制),且对于每个点(除源点、汇点),流入该点的“水量”等于该点流出的“水量”(流守恒性)。
其次网络流具有斜对称性,即对于一条边,若它的流量为f,则它的反向边流量为 -f。
(下面简写源点为Begin,汇点为End,网络的边集为 E、点集为 V)
用式子的方法总结一下网络流所具有的性质:
定义\(f(u,v)\)表示u到v的边的流量,\(c(u,v)\)表示u到v的边的流量限制(容量);只对相邻的 u,v 有此定义。
定义网络流的 流f 为:\(f=\sum_v f(Begin,v)=\sum_w f(w,End)\)
定义u到v的边的残留容量r(u,v)为:\(r(u,v)=c(u,v)-f(u,v)\)
最大流即流网络中的最大流值。
EK算法是对Ford-Fulkerson方法的实现。
『Ford-Fulkerson方法』
「残留网络&增广路」
如果 \(r(u,v)>0\),则边 (u,v) 在残留网络中。
增广路是残留网络中从 Begin 到 End 的一条路径 P,\(\delta(P)=\min\{r(u,v)\},(u,v)\in P\) 表示增广路P的残留容量。
「方法」
Ford-Fulkerson方法的主要思想是先构造残余, DFS 找到一条增广路,然后找到增广路上的流量 \(\delta\),将增广路上的每一条边的流量限制都减去 \(\delta\)、每一条边都反向边都流量限制都加上 \(\delta\) 。
为什么要把反向边的流量限制加上 \(\delta\) 呢?我们来看一个简单的例子:
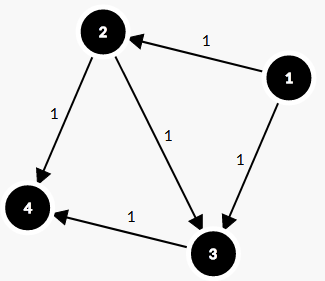
如果我们一开始选择流“1-2-3-4”,那么我们得到流的大小为1,但是显然我们可以选择流“1-2-4 , 1-3-4”,流的大小为2。
如果先流“1-2-3-4”,那么我们就相当于确定了边 (2,3) 必须流,但是这是不一定的。我们给它的反向边 (3,2) 加上 \(\delta\)(最初所有边的反向边的流量限制都为0),那么下一次我们流过它的反向边 (3,2) 时,就相当于“撤销”了流过 (2,3)。然后两次的流量之和就是最大流。
为什么这样是正确的?
让我们手推一下这张图的最大流过程:先找到了“1-2-3-4”,然后 (1,2)(2,3)(3,4) 的流量限制减去10,(2,1)(3,2)(4,3) 加上10;再流过 “1-3-2-4”。就相当于把原来“1-2-3-4”的(2,3)断开,接上(2,4)形成“1-2-4”;而断开过后的“2-3-4”中,流过反向边(3,2)使得(2,3)的流被撤销,再接上(1,3)就形成“1-3-4”。
『EK算法』
一种比较基础的对Ford-Fulkerson方法的实现,基于BFS。
首先定义一些数组,方便后面阐述:
(1) vis[u] 表示点 u 在该次BFS中是否被访问过
(2) flw[u] 表示该次BFS中从源点开始流到点 u 的流最大的值(也就是源点BFS到u的路径上的边的最小的流量限制)
(3) preedg[u] 表示该次BFS中是从哪一条边流到u的
「BFS部分」
从源点开始,BFS遍历整个流网络,要求经过的有向边的流量限制严格大于0,并且不重复经过同一个点。当遍历到汇点时,返回当前流值。
假设现在要从u流到v,先要保证 vis[v] == 0 并且 (u,v) 的流量限制大于0。然后标记 vis[v] ,再记录 preedg[v] 为当前边的编号;flw[v] 的计算类似于 dp,因为流值最大不超过 (u,v) 的限制,那么递推式也非常显然 \(flw[v]=\min\{flw[u],c(u,v)\}\)。
如果v就是汇点,则返回 flw[v],否则将v压入队列。
如果最后无法到达汇点,则返回0,表示无增广路。
「EK算法主部分」
先BFS判断当前是否有增广路,如果有,则BFS返回值则为增广路的流量 \(\delta\),则从v沿着增广路倒过来回到源点,并将增广路上的边的流量限制减去 \(\delta\),增广路上的边的反向边的流量限制加上 \(\delta\) 。直到没有增广路(BFS返回值为0),退出循环。
其实就是把 Ford-Fulkerson 方法模拟了一遍。
因此EK算法的时间复杂度并不理想,但毕竟它是(似乎是)最大流算法中最为稳定的算法,有其存在的价值。
「模板代码」
以〔洛谷 P2740〕为原题的代码~
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N=200;
struct FLOWGRAPH{
struct NODE{
int to,nxt,lim,rev;
NODE(){}
NODE(int _to,int _nxt,int _lim,int _rev):
to(_to),nxt(_nxt),lim(_lim),rev(_rev){}
}nod[N*2+7];
int cnt,adj[N+7];
void Rebuild(){
memset(adj,-1,sizeof adj);
cnt=0;
}
void AddEdge(int u,int v,int lim){
int A=++cnt,B=++cnt;
nod[A]=NODE(v,adj[u],lim,B),adj[u]=A;
nod[B]=NODE(u,adj[v],0,A),adj[v]=B;
}
}grp;
int m,n;
int preedg[N+7],flw[N+7],vis[N+7];
int BFS(int cas){
queue<int> que;
que.push(1);
flw[1]=(1<<30);
while(!que.empty()){
int u=que.front();que.pop();
for(int i=grp.adj[u];i!=-1;i=grp.nod[i].nxt){
int v=grp.nod[i].to;
if(!grp.nod[i].lim || vis[v]==cas) continue;
vis[v]=cas;
preedg[v]=i;flw[v]=min(grp.nod[i].lim,flw[u]);
if(v==n) return flw[v];
que.push(v);
}
}
return 0;
}
int EK(){
int del,res=0,cas=0;
while(del=BFS(++cas)){
int pnt=n;
while(pnt!=1){
grp.nod[preedg[pnt]].lim-=del;
grp.nod[grp.nod[preedg[pnt]].rev].lim+=del;
pnt=grp.nod[grp.nod[preedg[pnt]].rev].to;
}
res+=del;
}
return res;
}
int main(){
grp.Rebuild();
scanf("%d%d",&m,&n);
for(int i=0;i<m;i++){
int u,v,lim;
scanf("%d%d%d",&u,&v,&lim);
grp.AddEdge(u,v,lim);
}
int res=EK();
printf("%d\n",res);
return 0;
}
\(\mathcal{The\ End}\)
\(\mathcal{Thanks\ For\ Reading!}\)
如果有没看懂或者有问题的,请咨询作者邮箱\(lucky\_glass@foxmail.com\)~


