竞赛题解 - [CF 1080D]Olya and magical square
Olya and magical square - 竞赛题解
借鉴了一下神犇tly的博客QwQ(还是打一下广告)
终于弄懂了
Codeforces 传送门
『题目』(直接上翻译了)
给一个边长为 \(2^n(n>0)\) 的正方形,你需要对它进行恰好 \(k(k>0)\) 次“剪切”,“剪切”的方法是:选取一个边长不为 \(1\) 的正方形,将它剪成 \(4\) 个大小相同的正方形,不能挪动位置。
要求在 \(k\) 次操作后存在一条路径:从左下角的正方形到右上角的正方形,且路径上所有正方形的大小都相等。
求是否可行,若存在可行解,输出可行解的路径上的正方形的边长以 \(2\) 为底的对数。
『解析』
其实比较容易看出来是一道结论(找规律)题,毕竟也就只有这种类型之类的题会把 \(k\) 设置为 \(10^{18}\) 这么大……
大概的解题思路是:对于每一种可能的路径上正方形的边长 \(2^i\),求出这种情况最少需要进行多少次剪切以及最多需要多少次,判断 \(k\) 是否在这个区间内。
不妨让路径先一直向上,然后一直向右。假设现在路径上正方形的边长是 \(2^i\),
- 先求一下最少次数
这种情况的最少操作次数为 \(1+3+7+...+(2^i-1)\),感性理解一下——
当 \(i=n-1\) 时显然最少需要进行 \(1\) 次操作,这样就会变成:
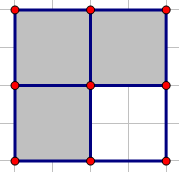
如果进一步让 \(i=n-2\),那么我们就应该对上图的灰色块进行操作,也就是 \(3\) 次。……以此类推,就会得到上面的式子~ - 然后求最大次数
显然(一般来说)在最少次数的基础下我们还可以再进行一些不会对答案造成影响的操作——也就是对除了左下角到左上角再到右上角的路径上的正方形(最左边、最上边的正方形),我们最多可以把它们全部剪成\(1*1\)的~
令 \(f(siz)\) 为将边长为 \(2^{siz}\) 的正方形剪成 \(1*1\) 的操作次数,那么我们发现 \(2^{siz}\) 的边长剪 \(1\) 次会变成 \(4\) 个 \(2^{siz-1}\),再剪 \(4\) 次会变成 \(16\) 个 \(2^{siz-2}\)……
以此类推,我们可以得到 \(f(siz)=1+4+4^2+...+4^{siz-1}\) 。
假设现在正方形的边长为 \(2^a\),左上角的正方形为 \(2^b(b<a)\),如果按照最小方法剪,那么正方形可能长这样:

上面的蓝色部分就是我们可以乱剪(不会对答案造成影响)的正方形,假设我们已经算出来了这一块蓝色部分全部剪成 \(1*1\) 的操作次数,然后如果按照最小方法继续剪,它就会变成这样:
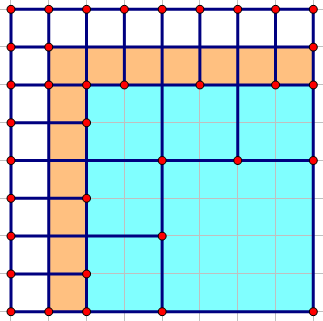
上面的橙色部分就是相较上一次剪切多出来的可以任意操作而不会影响答案的正方形(假设它们的大小不是 \(1*1\)),那么我们要算这一次可以任意剪切的次数就可以根据上一次(蓝色部分)加上这次(橙色部分)全部剪成 \(1*1\) 的操作次数~
而我们发现橙色正方形的边长就是我们的路径上的正方形边长,所以可以直接套用 \(f()\) 函数计算。至于个数……假设上一次多出来的正方形(蓝色里面除去右下角的正方形)的个数为 \(tmp'\) ,那么这次多出来的正方形个数就是 \(tmp=(tmp-1)*4+5\),找规律嘛~
那么最大操作数就是最少操作数加上将这些(橙色和蓝色)正方形剪成 \(1*1\) 的正方形的操作数。
那么我们只要枚举一下答案的路径上的正方形边长,判断 \(k\) 是否在最小操作数和最大操作数之间即可。但是我们可以看到 \(n\) 也不小……所以这里还有一个 特性:
当 \(n \geq 32\) 时,答案就是 \(n-1\)
为什么?显然如果我们要将边长为 \(2^m(m \geq 31)\) 的正方形全剪成 \(1*1\) 的正方形的总操作次数已经超过了 \(10^{18}\) ,这就意味着我们可以将原来 \(n \geq 32\) 的正方形剪成 \(4\) 个边长为 \(2^{n-1}\) 的正方形,然后就尽可能地将右下角的那一个边长为 \(2^{n-1}\) 的正方形剪成 \(1*1\) 的,但是 \(k\) 并不够大,所以就可以将剩下的 \(k-1\) 次机会全部用完~
代码比较简单,但是论证思路还是非常严谨的!
『源代码』
/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll QPow(ll a,int r){ //快速幂
ll res=1ll;
while(r){
if(r&1) res*=a;
a*=a;
r>>=1;
}
return res;
}
ll Cut(int siz){ //把边长为 2^siz 的正方形剪成 1*1 的操作次数
return (QPow(4,siz)-1)/3;
}
int Solve(int n,ll k){
if(n>=32) return n-1;
else{
ll liml=0,limu=0,sam=1;
//liml:最少操作次数
//limu:在最少操作次数的基础上最多还能进行的操作次数使得答案不变化
//sam:按最少操作方法与路径上的正方形大小相同的正方形(除去路径上的)的最大个数,也就是进行最少操作后相较上一次多出来的可以任意操作的正方形的个数
for(int i=n-1;i>=0;i--){
liml+=(1<<n-i)-1;
limu+=sam*Cut(i);
sam=(sam-1)*2+5;
if(liml<=k && k<=limu+liml) //是否在范围内
return i;
if(k<liml) return -1;
}
}
return -1;
}
int main(){
int cas;scanf("%d",&cas);
while(cas--){
int n;ll k;
scanf("%d%lld",&n,&k);
int res=Solve(n,k);
if(res==-1) printf("NO\n");
else printf("YES %d\n",res);
}
return 0;
}
\(\mathfrak{THE\ END}\)
\(Thanks\ for\ reading!\)
没看懂的可以在 \(lucky\_glass@foxmail.com\) 随便问~


