首先,假设3维曲面函数表示成 z = f(x, y), 那么等高面可以表示为在 z = c时的切平面。将该切平面向xoy平面的投影,投影的轮廓便是等高线:
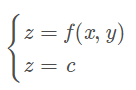
直观表示为,每一条虚线都表示一个等高线
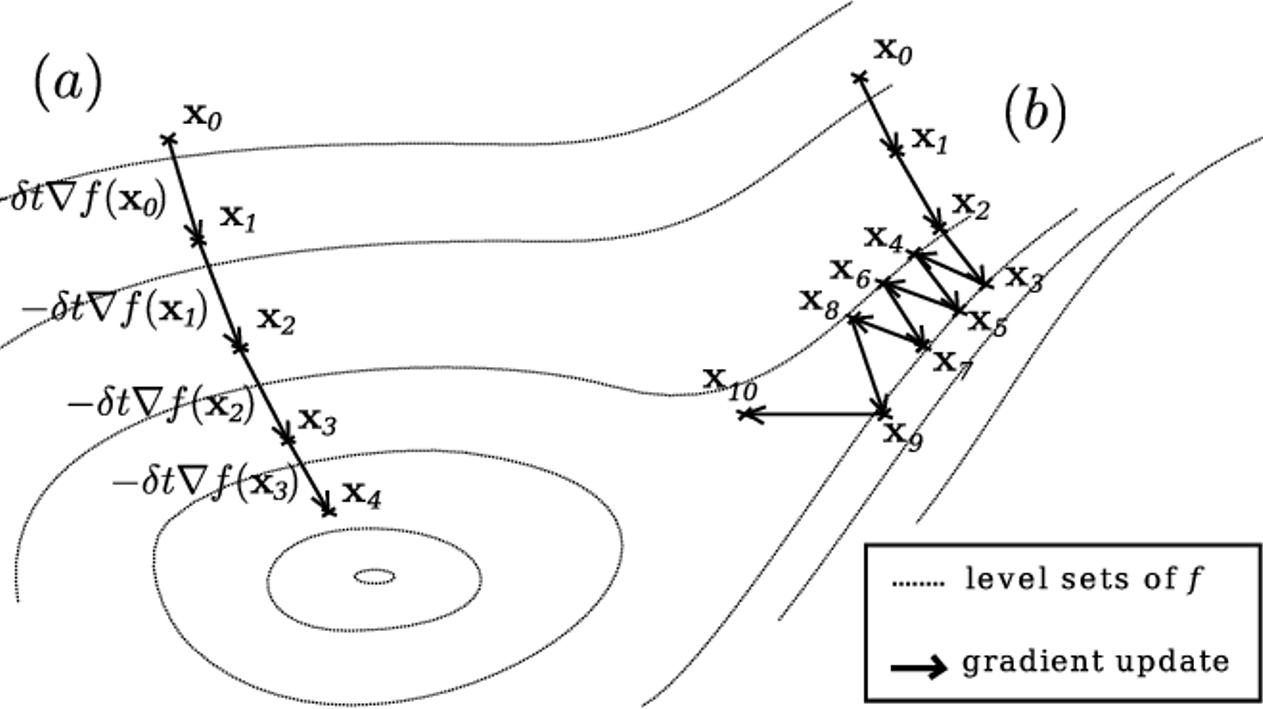
在上图中,(a)路径的x0位置处的切线斜率表示为dy/dx,与切线斜率垂直的法线斜率表示为:
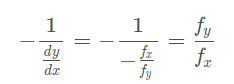
因为 f(x, y) = c是隐函数,即y是x的函数,等号两边对x求导表示为:
f'_x * dx + f'_y * dy/dx * dx = 0,所以 dy/dx = - f'_x / f'_y
又,函数f(x,y)=c的梯度表示成 f_x * i + f_y * j,方向为 f_y / f_x 所以看出,梯度方向与切线垂直方向是相同的。
注意:梯度指向函数值增大最快的方向,所以梯度的反方向指向函数值减小最快的方向
参考:https://blog.csdn.net/bitcarmanlee/article/details/85275016
https://www.cnblogs.com/shine-lee/p/11715033.html





