洛谷P1070 道路游戏(dp+优先队列优化)
题目链接:传送门
题目大意:
有N条相连的环形道路。在1-M的时间内每条路上都会出现不同数量的金币(j时刻i工厂出现的金币数量为val[i][j])。每条路的起点处都有一个工厂,总共N个。
可以从任意工厂i购买机器人,价格为cost[i]。机器人可以设定为从购买的工厂开始顺时针行走长度为1-P的任意时间,并在这段时间内在路上收集金币。
小新能且只能同时拥有一个机器人,当一个机器人行走结束后小新会立即从任意一个工厂内买一个新的机器人,设定时间,并继续顺时针收集。
问M时间内最多能收集多少金币。
2 ≤ N ≤ 1000, 1 ≤ M ≤ 1000, 1 ≤ P ≤ M,各种金额都为1-100间的整数。
假思路1.0(折叠失败:-D):
//92分O(n3)不看题解只能搓出这种拙劣的算法:
//不想看花里胡哨的思路可以直接跳到思路2.0 (-。=)
因为每个时刻j每个工厂i都可以选择买一个机器人或者不买机器人。
①如果买了就可以用于更新之后的1-P时间;
②如果不买就只能从之前k(1≤k≤P)时间内的买了局面更新过来。
注意:从之前的k时间内更新过来的时候需要依次加上之前1-k时间内机器人经过的路径上的所有金币,这里需要预处理一个前缀和sum。
状态:
f[i][j][2]表示j时刻到第i个工厂的最大金额,第三维表示此时此地有没有买机器人,0表示没买,1表示买了。
初始状态:
memset(f, -INF, sizeof f);
f[i][0][0] = 0;
f[i][0][1] = -cost[i+1];
//cost[i+1]是因为此时此地的金额若用于更新未来的时刻,应从路的终点而不是起点购买机器人,
因为这条路的金币已经被收集了,说明机器人已经走过了这条路到达了这条路经的终点。
如:更新f[2][1][0]的时候会从f[2-1][1-1][1] = f[1][0][1]处更新,这里i=1,但是实际上需要购买i+1 = 2处的机器人。
状态转移方程:
f[i][j][0] = max(f[i][j][0], f[i-k][j-k][1] + j-k时刻在第i-k个工厂处经过k时间到达(j,i)处的累计金币);
f[i][j][1] = max(f[i][j][1], f[L][j][0] - cost[i+1]);
//这里的L遍历了j时刻所有的工厂为找出最大值。cost[i+1]同上。
时间复杂度: O(MN2)

#include <bits/stdc++.h> using namespace std; const int INF = 0x3f3f; const int MAX_N = 1e3 + 5; #define ind(x) ((x+N-1)%N+N)%N+1 int N, M, P; int f[MAX_N][MAX_N][2];//0表示不走,1表示走 int cost[MAX_N], val[MAX_N][MAX_N], sum[MAX_N][MAX_N]; inline int cal(int i, int j, int k) { return sum[i][j] - sum[ind(i-k)][j-k]; } int main() { //92分 cin >> N >> M >> P; for (int i = 1; i <= N; i++) for (int j = 1; j <= M; j++) scanf("%d", &val[i][j]); for (int i = 1; i <= N; i++) scanf("%d", cost+i); for (int j = 1; j <= M; j++) for (int i = 1; i <= N; i++) sum[i][j] = sum[ind(i-1)][j-1] + val[i][j]; for (int i = 0; i <= N; i++) for (int j = 0; j <= M; j++) f[i][j][0] = f[i][j][1] = -INF; for (int j = 0; j <= M; j++) { for (int i = 1; i <= N; i++) { if (j == 0) { f[i][j][0] = 0; f[i][j][1] = f[i][j][0] - cost[ind(i+1)]; } for (int k = 1; k <= min(P, j); k++) { if (j-k < 0) break; f[i][j][0] = max(f[i][j][0], f[ind(i-k)][j-k][1] + cal(i, j, k)); } } for (int i = 1; i <= N; i++) { for (int l = 1; l <= N; l++) { f[i][j][1] = max(f[i][j][1], f[l][j][0] - cost[ind(i+1)]); } } } int ans = -INF; for (int i = 1; i <= N; i++) ans = max(ans, f[i][M][0]); cout << ans << endl; return 0; } /* 2 2 1 1 2 2 3 1 1 */
假思路1.1(折叠失败×2 :-D):
//100分O(n3)卡过,在TLE的边缘试探(滑稽)
在思路1.0中的状态转移方程中有:
f[i][j][1] = max(f[i][j][1], f[L][j][0] - cost[i+1]);
我枚举l遍历了所有工厂,然鹅这实际上是没有必要的。我们可以直接把所有工厂的最大值保留下来,而不是一一枚举。
因为无论是未来的时刻从j时刻转移,还是最后统计答案,我们都只会用到j时刻所有工厂中的最大金币数,所以非最大值的保留是没有意义的,第二维,去掉。
去掉了原状态的第二维,我们仔细思考可以发现第三维的0和1也是可以去掉的:
如果未来从j时刻转移了,直接在转移时减掉对应的cost即可,而不需要一一保存减掉cost之后的值。
状态:
f[i]表示i时刻所有工厂中的最大金币数。
初始状态:
显然f[0] = 0;//没开始走就没有钱。
状态转移方程:
f[i] = max(f[i], f[i-k] + i-k时刻在第j-k个工厂处经过k时间到达(i,j)处的累计金币 - cost[j+1-k]);
//这里的累计金币同样需要预处理前缀和。
去掉了两个维度,也免去了遍历L产生的硬性O(n),变成了1-P的不完全O(n),752ms偷渡成功。
时间复杂度: O(MNP)

#include <bits/stdc++.h> using namespace std; const int INF = 0x3f3f3f; const int MAX_N = 1e3 + 5; #define ind(x) ((x-1)%N+N)%N+1 int N, M, P; int val[MAX_N][MAX_N], cost[MAX_N], sum[MAX_N][MAX_N]; int f[MAX_N]; inline int cal(int x, int y, int z) { return sum[x][y] - sum[ind(x-z)][y-z]; } int main() { //100分O(n^3)卡过 cin >> N >> M >> P; for (int i = 1; i <= N; i++) for (int j = 1; j <= M; j++) scanf("%d", &val[i][j]); for (int i = 1; i <= N; i++) scanf("%d", cost+i); for (int j = 1; j <= M; j++) for (int i = 1; i <= N; i++) sum[i][j] = sum[ind(i-1)][j-1] + val[i][j]; for (int j = 1; j <= M; j++) f[j] = -INF; f[0] = 0; for (int i = 1; i <= M; i++) { for (int j = 1; j <= N; j++) { for (int k = 1; k <= P; k++) { if (i < k) break; f[i] = max(f[i], f[i-k] + sum[j][i] - sum[ind(j-k)][i-k] - cost[ind(j-k+1)]); } } } cout << f[M] << endl; return 0; }
思路2.0(没想到你真的就直接来看正解了(〃>皿<)):
//O(n2logn),题目的数据范围是1000,O(n3)卡过的题就是感觉不爽。于是就有了以下的解法
(敲黑板!!!)
首先我们可以这样理解对机器人步数的设定:在开始行走之后的1-P时间内,我们可以在任意时刻打断它,然后买一个新的机器人。
所以对于时刻i,如果此时的机器人是在i-k时刻买的,则时刻i的累计金币,等于i-k时刻的累计金币,加上机器人从i-k时刻走到i时刻累计得到的金币,减去i-k时刻购买机器人花费的金币。
这里的“机器人从i-k时刻走到i时刻累计得到的金币”,预处理前缀和sum后就可以直接算出。
于是有状态:
f[i]表示i时刻的最大累计金币。
初始状态:
显然f[0] = 0;//没开始走就没有钱。
状态转移方程:
f[i] = max(f[i], f[i-k] + sum[j][i] - sum[j-k][i-k] - cost[j-k+1]);
但是这样转移会有很多重复计算!
如图:
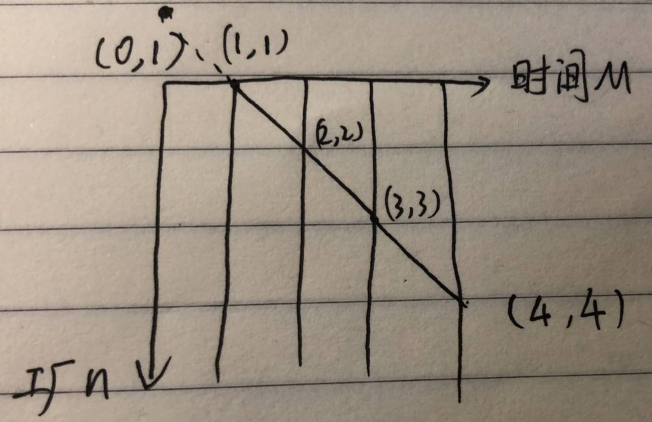
在更新点(3,3)的时候已经计算过了点(1,1)和点(2,2)转移到点(3,3)的值,而这个值仅与起点和终点有关。
我们可以把只与起点有关的值分离出来,就可以免去枚举起点的复杂度了:
①转移之前的状态只与起点有关,分离之;
②转移时的cost只与起点有关,分离之;
③转移时的累计金币是通过前缀和计算的:
sum[j][i] - sum[j-k][i-k],
//这里的sum[j-k][i-k]只取决于起点,分离之。sum[j][i]取决于终点,那就不动。
把这些分离出来的值合起来放到优先队列里面:
对于起点(i, j) 构造一个data[i][j] = f[i] - sum[j][i] - cost[j+1];
那么当从起点(i-k, j-k) 更新到点(i, j)时,f[i] = max(f[i], data[i-k][j-k] + sum[j][i]);
发现对于所有的k(1 ≤ k ≤ P),只需要取出data[i-k][j-k]中的最大值,拿来更新f[i]即可。
将这些所有data装入(对应斜行的)优先队列中,就可以用O(logn)的时间从优先队列里拿出最大值了 ♪(^∀^●)ノ
lei了lei了:新的状态转移方程:
f[i] = max(f[i], max(data) + sum[j][i]);
时间复杂度: O(MNlogN)

#include <bits/stdc++.h> using namespace std; const int INF = 0x3f3f3f; const int MAX_N = 1e3 + 5; #define ind(x) ((x-1)%N+N)%N+1 struct Node{ int data, t; Node(int _d = 0, int _t = 0) : data(_d), t(_t) {} bool operator < (const Node& x) const { return data < x.data; } }; int N, M, P; int val[MAX_N][MAX_N], cost[MAX_N], sum[MAX_N][MAX_N]; int f[MAX_N]; inline int cal(int x, int y, int z) { return sum[x][y] - sum[ind(x-z)][y-z]; } priority_queue <Node> Q[MAX_N]; int main() { cin >> N >> M >> P; for (int i = 1; i <= N; i++) for (int j = 1; j <= M; j++) scanf("%d", &val[i][j]); for (int i = 1; i <= N; i++) scanf("%d", cost+i); for (int j = 1; j <= M; j++) for (int i = 1; i <= N; i++) sum[i][j] = sum[ind(i-1)][j-1] + val[i][j]; for (int j = 1; j <= M; j++) f[j] = -INF; f[0] = 0; for (int i = 0; i <= M; i++) { if (i != 0) for (int j = 1; j <= N; j++) { while (!Q[ind(i-j)].empty() && i - Q[ind(i-j)].top().t > P) Q[ind(i-j)].pop(); Node cur; if (!Q[ind(i-j)].empty()) cur = Q[ind(i-j)].top(); f[i] = max(f[i], cur.data+sum[j][i]); } for (int j = 1; j <= N; j++) { Node cur(f[i]-sum[j][i]-cost[ind(j+1)], i); Q[ind(i-j)].push(cur); } } cout << f[M] << endl; return 0; }




