Codeforces Round #516(Div 2)
比赛链接:传送门
A. Make a triangle!(简单思维)
题目大意:
给你三条边,问你最多加多少长度能使这三条边能构成三角形。
思路:
最大边小于答案加另外两条边的和。

#include <bits/stdc++.h> using namespace std; int main() { int a, b, c; cin >> a >> b >> c; int _max = max(a, b); _max = max(_max, c); int sum = a+b+c - _max; int ans = max(0, _max-sum+1); cout << ans << endl; return 0; }
B. Equations of Mathematical Magic(位运算)
题目大意:
给定a,求方程:a = x + (a^x)的非负整数解的数量。(符号"^"表示异或)
思路:
只有一个二进制位时:(表达式各位置的对应未知数与上面方程对齐)
① a = 0:0 = 0 + (0^0)
② a = 1:1 = 0 + (1^0) = 1 + (1^1)
所以对于题目a的每个二进制位:
① 如果为0,则x的对应二进制位也只能为0
② 如果为1,则x的对应二进制位可以是1或0
组合后答案为2k,(其中k为a变成二进制后1的个数)

#include <bits/stdc++.h> using namespace std; int main() { int T; cin >> T; while (T--) { int N; cin >> N; int cnt = 0; while (N) { if (N&1) cnt++; N/=2; } cout << (1 << cnt) << endl; } return 0; } /* 3 0 2 1073741823 */
C. Oh Those Palindromes(字符串)
题目大意:
求给定字符串重排序后,最多的回文子串数量。
思路:
把一样的字母放在一起貌似就可以了。(直接sort)

#include <bits/stdc++.h> using namespace std; int cnt[30]; int main() { int N; string s; cin >> N >> s; memset(cnt, 0, sizeof cnt); for (int i = 0; i < N; i++) { int ind = s[i] - 'a'; cnt[ind]++; } for (int i = 0; i < 26; i++) { while (cnt[i]--) { printf("%c", 'a'+i); } } printf("\n"); return 0; }
D. Labyrinth(0-1bfs)
题目大意:
给定bfs图,起始点,最多的左移次数X、右移次数Y,求能访问的最多的格子数。
思路:
用bfs乍一搜可以pretest passed,但是可以被这组样例hack。

/* 20 7 3 6 5 2 ......* .****.* .****.* ....*.* **.**.* **.**.* **.**.* **.**.* **.**.* **.**.* **.**.* **.**.* **.**.* **.**.* **.**.* **.**.* **.**.* **.**.* **....* ******* */
加一个对当前点X、Y的最大值的维护即可。
另外可以按列缩点跑最短路,不过我没试过。

#include <bits/stdc++.h> using namespace std; const int MAX_N = 2e3 + 5; const int actx[4] = {0, 0, 1, -1}; const int acty[4] = {1, -1, 0, 0}; struct Node{ int x, y; int resl, resr; Node(int xx = 0, int yy = 0, int ll = 0, int rr = 0) : x(xx), y(yy), resl(ll), resr(rr) {} }nodes[MAX_N][MAX_N]; int N, M, R, C, X, Y; char mat[MAX_N][MAX_N]; bool vis[MAX_N][MAX_N]; inline bool check(int x, int y) { if (x < 1 || x > N || y < 1 || y > M) return false; if (mat[x][y] == '*') return false; return true; } int main() { cin >> N >> M >> R >> C >> X >> Y; memset(vis, false, sizeof vis); for (int i = 1; i <= N; i++) scanf("%s", mat[i]+1); queue <Node> Q; vis[R][C] = true; Q.push(Node(R, C, X, Y)); while (!Q.empty()) { Node cur = Q.front(); Q.pop(); for (int i = 0; i < 4; i++) { int x = cur.x + actx[i]; int y = cur.y + acty[i]; if (!check(x, y)) continue; int l = cur.resl; int r = cur.resr; if (i == 0) r--; if (i == 1) l--; if (l < 0 || r < 0) continue; if (x == 4 && y == 4) int aaa = 1; if (vis[x][y]) { if (l > nodes[x][y].resl || r > nodes[x][y].resr) { nodes[x][y].resl = max(l, nodes[x][y].resl); nodes[x][y].resr = max(r, nodes[x][y].resr); } else continue; } else if (!vis[x][y]) { nodes[x][y] = Node(x, y, l, r); vis[x][y] = true; } Q.push(Node(x, y, l, r)); } } int ans = 0; for (int i = 1; i <= N; i++) { for (int j = 1; j <= M; j++) { if (vis[i][j]) ans++; } } cout << ans << endl; return 0; }
更新:
正解应该是0-1bfs(说白了就是用双向队列deque维护的bfs)
纵向搜到的点入队首,横向搜到的点入队尾。

#include <bits/stdc++.h> using namespace std; const int MAX_N = 2000 + 5; const int actx[4] = {1, -1, 0, 0}; const int acty[4] = {0, 0, 1, -1}; #define nx cur.x+actx[i] #define ny cur.y+acty[i] struct Node{ int x, y; int l, r; Node (int xx = 0, int yy = 0, int ll = 0, int rr = 0) : x(xx), y(yy), l(ll), r(rr) {} }; int N, M, R, C, X, Y; bool vis[MAX_N][MAX_N]; char mat[MAX_N][MAX_N]; bool check(int x, int y) { if (x < 1 || x > N || y < 1 || y > M) return false; if (mat[x][y] == '*' || vis[x][y]) return false; return true; } int bfs0_1() { int ans = 1; memset(vis, false, sizeof vis); deque <Node> Q; Q.push_back(Node(R, C, X, Y)); vis[R][C] = true; while (!Q.empty()) { Node cur = Q.front(); Q.pop_front(); for (int i = 0; i < 4; i++) { if (!check(nx, ny)) continue; int l = cur.l; int r = cur.r; if (i < 2) { Q.push_front(Node(nx, ny, l, r)); } else { if (i == 2) r--; if (i == 3) l--; if (l < 0 || r < 0) continue; Q.push_back(Node(nx, ny, l, r)); } vis[nx][ny] = true; ans++; } } return ans; } int main() { cin >> N >> M >> R >> C >> X >> Y; for (int i = 1; i <= N; i++) scanf("%s", mat[i]+1); cout << bfs0_1() << endl; return 0; }
E. Dwarves, Hats and Extrasensory Abilities(二分)
题目大意:
交互式的题目,给定N,然后你输出N个点的坐标,你每输出一个点,他给你这个点的颜色(随机黑或白),然后让你给出一条直线,使得黑白的点在线的两边。
思路:
二分坐标系。注意题目中坐标系的上限直接拿来用的话,不够N的最大值。
所以有下图的二分选择:

注意交互式的题目输出时要加一个cout << flush;

#include <iostream> using namespace std; int main() { int N; cin >> N; int l = 0, r = 1 << 29; string sl, scur; cout << l << ' ' << l << endl << flush; cin >> sl; if (N == 1) { cout << 1 << ' ' << 0 << endl << flush; cout << 1 << ' ' << 1 << endl << flush; return 0; } cout << r << ' ' << 0 << endl << flush; cin >> scur; N -= 2; if (sl == scur) {//在(2^29, 0)到(2^29, 2^29)内二分 int mid = (l + r) >> 1; int x = 1 << 29; while (N--) { cout << x << ' ' << mid << endl << flush; cin >> scur; if (scur == sl) l = mid; else r = mid; mid = (l + r) >> 1; } cout << x << ' ' << mid << endl << flush; cout << x-1 << ' ' << mid << endl << flush; } else { int mid = (l+r) >> 1; int y = 0; while (N--) { cout << mid << ' ' << y << endl << flush; cin >> scur; if (sl == scur) { l = mid; } else { r = mid; } mid = (l+r) >> 1; } cout << mid << ' ' << y << endl << flush; cout << mid << ' ' << y+1 << endl << flush; } return 0; }
更新:
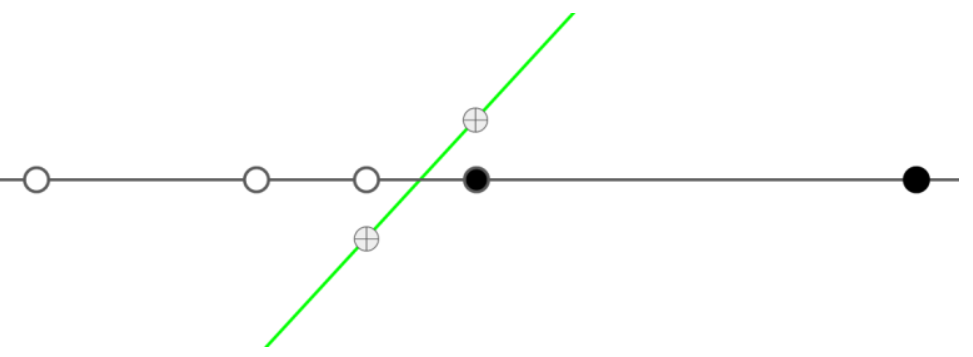
在x轴上二分也可以。

#include <iostream> using namespace std; void print(int x, int y) { cout << x << ' ' << y << endl << flush; } int main() { int N; string col, pre; cin >> N; int l = 0, mid = 0, r = 1<<29; if (N--) { print(l, 1); cin >> pre; mid = (l+r) >> 1; } while (N--) { print(mid, 1); cin >> col; if (col == pre) l = mid; else r = mid; mid = (l+r) >> 1; } print(l, 0); print(r, 2); return 0; }
F. Candies for Children(数学+分类暴力)
题目大意:
有n个人围成一圈分k个糖果,从 l 开始分到 r ,可以跑很多圈。一个人拿一颗,里面有p个人喜欢甜食会拿两颗。
问你p的最大值。数据矛盾则输出-1。
思路:
题目中的数据范围是1e11,这个数据很微妙(1e11 = 1e5 * 1e6),所以分两种情况讨论:
① n < 2e6 :
这时候可以直接跑答案。
对于给定的p,y有很多取值,但是可以直接取模算出y的满足p、d约束最大值。O(n)复杂度。
② n > 2e6 :
这时候跑圈数i,每个对应的圈数可以求出最大的喜欢甜食的人数:
1、(p + n) * i + y + d = k
2、p - y <= n - d
联立这个就可以求p的最大值。(其中d表示l跑到r的人数,y表示d中的喜甜人数)然后处理一下细节就可以O(k/n)。
然后暴力跑就好了。注意一个点就是最后一个人可以喜欢甜食但是只拿一个。

#include <bits/stdc++.h> using namespace std; typedef long long ll; const ll X = 2e6 + 5; int main() { ll n, l, r, k; cin >> n >> l >> r >> k; ll d = (r - l + n) % n + 1; ll ans = -1; if (n < X) { for (ll p = n; p >= 0; p--) { ll y = (k - 1)%(n + p) + 1 - d; if (y < 0 || y > p || y > d || d-(y+1) > n-p) continue; ll y2 = y+1; if (y2 <= p && y2 <= d) { ans = max(ans , p); } if (d-y <= n-p) { ans = max(ans, p); } } } else { for (ll i = 0; i <= k/n; i++) { ll p = (k - 2*d - (i-1)*n + 1) / (i+1); ll y = k - i*(n+p) - d; if (y < 0) { if (i == 0) continue; ll dis = (-y - 1) / i + 1; y += i*dis; p -= dis; } if (p > n) { y += (p-n) * i; p == n; } if (y < 0 || y > p || y > d || d-(y+1) > n-p) continue; ll y2 = y+1; if (y2 <= p && y2 <= d) { ans = max(ans , p); } if (d-y <= n-p) { ans = max(ans, p); } } } cout << ans << endl; return 0; } /* 10 5 5 1 10000000 5 5 1 */



