栈的应用
一、数制转换
例如,把十进制数159转换成八进制数,如图
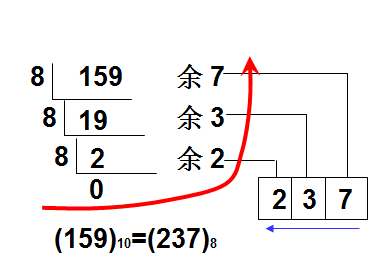
159/8=19余7,19/8=2余3,2/8=0余2,我们发现得到的结果是倒过来的,因为栈的先进后出的特性,所以可以用栈来存储这几个数,然后输出出来就是对应的正确的八进制数了。
伪代码:
void conversion(){
InitStack(&S);//构造一个空栈S
scanf("%d",&n);
while(n){
push(&S,n%8);//把余数进栈
n=n/8;
}
while(!StackEmpty(S)){
Pop(&S,&e);//倒着输出,即出栈,得到的余数
printf("%d",e);
}
}//conversion
二、括号匹配的检验
即检验括号是否一一对应,如[ ( ) [ ] ]为正确的格式,( [ ] ( )为错误的格式。
算法描述:
读入表达式,若遇到左括号进栈,若遇到右括号则检验栈顶元素是否和右括号匹配,若匹配则出栈,若不匹配则表达式格式错误。若读完所有的括号,栈为空,则表达式格式正确,栈不为空则表达式格式错误。
伪代码:
Status matching(char exp[]){
InitStack(&S);
for(i=0;i<Length(exp);i++){
if(exp[i]=='('||exp[i]=='[')
Push(&S,exp[i]);
else if(exp[i]==')'||exp[i]==']'){
if(StackEmpty(S))
return ERROR;
Pop(&S,e);
if(e!=exp[i]){
exit ERROR;
}
}//for
if(StackEmpty(S))
return OK;
else
return ERROR;
}//matching
三、行编辑程序问题
设立一个输入缓冲区,用以接受用户输入的一行字符,然后逐行存入用户缓冲区,并假设“#”为退格符,“@”为退行符。例如,
whli##ilr#e( s#*s )
outcha@putchar(*s=#++);
实际有效的是如下两行
while(*s)
putchar(*s++);
算法描述:
1、既不是退格符也不是退行符,则入栈。
2、退格符,栈顶元素出栈。
3、退行符,清空栈。
四、迷宫求解问题,广度优先搜索(BFS)。
五、表达式求值
中缀表达式转后缀表达式和前缀表达式:
推荐链接:
①http://blog.csdn.net/antineutrino/article/details/6763722/
1)计算后缀表达式
算法描述:读入表达式,从左到右读,遇到数字则入栈,遇到操作符,则连续从栈顶退出两个元素,计算结果入栈,当表达式所有项处理完后,栈顶元素即为最后计算结果。
伪代码:
double calcul_exp(char a[]){
InitStack(&S);
for(i=0;i<Length(a);i++){
if(a[i]!='+'&&a[i]!='-'&&a[i]!='*'&&a[i]!='/'&&a[i]!='%'){
Push(&S,a[i]);
}//if
else{
Pop(&S,a);
Pop(&S,b);
switch(a[i]){
case '+' : c=a+b;break;
case '-' : c=a-b;break;
case '*' : c=a*b;break;
case '\' : c=a/b; break;
case '%' : c=a%b; break; }//switch
Push(&S,c);
}//else
}//for
PopStack(&S,result);
return result;
}//calcul_exp
2)计算前缀表达式
算法描述:从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算,并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果。
伪代码:
和计算后缀表达式一样,只不过for循环i从Length(a)开始到0。



