主席树
主席树
upd2022.8.10再开个新坑,以后填上
upd2022.8.11
历史:主席树又叫可持久化线段树,为什么?因为它比较持久,先说说它为什么叫主席树吧,因为主席树创始人叫\(黄嘉泰\),缩写\(hjt\),是不是很像某个人的名字,所以民间就叫它主席树了,
那么主席树是什么呢?
主席树,即可持久化线段树,支持对每个历史版本的访问,而在实际应用中,主席树近似为一种思想,即对每个位置建一棵线段树,并且优化空间。
该如何使用主席树呢?
例如我们要维护每个历史版本的情况,那么我们的朴素处理方法是对每个历史版本建一棵线段树,占用区间极大。而拿单点修改的操作举例,不难发现,每次改变的线段树上节点,也仅仅是一条链,所以我们只需要在上一个版本的基础上,将这一条链新开点赋值,就能够节省许多空间。之后的操作就和线段树相同了
举个栗子:
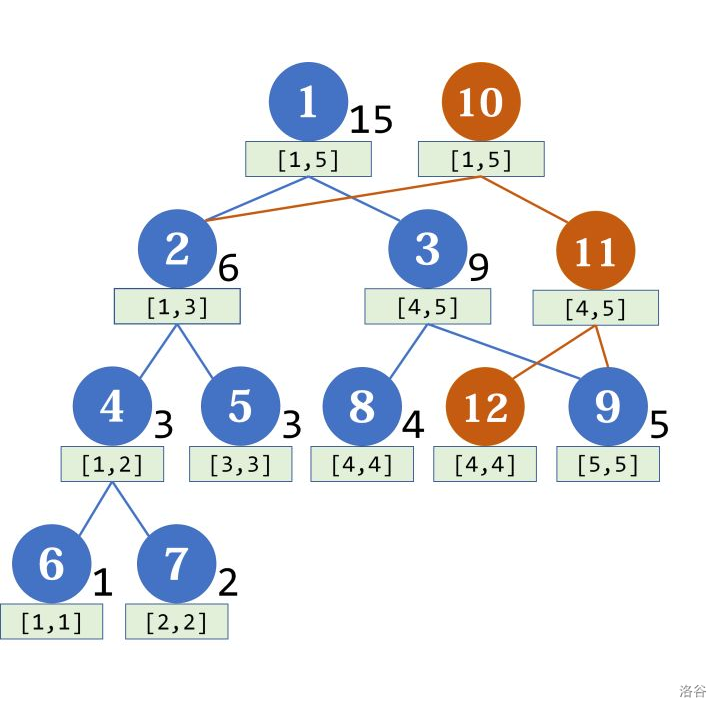
假设原始数据是\(1,2,3,4,5\),那我们就有了以下的一颗线段树(\(root[1]\)为根)

然后维持这棵树不变,额外添加节点来操作;
单点修改:
现在我们令\(A4\)加\(2\),然后创建一个新的根节点\(root[2]\)

要修改的\(A4\)对应的节点在柚子树上,所以这个树的新节点的左儿子应该和\(root[1]\)的左儿子相同,再建一个新的节点当改变的右儿子\(A4'\),接下来处理这个新节点(这是一个递归的过程),显然\(A4\)应该在左子树,所以相似地,沿用原树的右儿子,然后创建一个新的节点作为左儿子。
节点来给每个节点赋值,和线段树一样了就
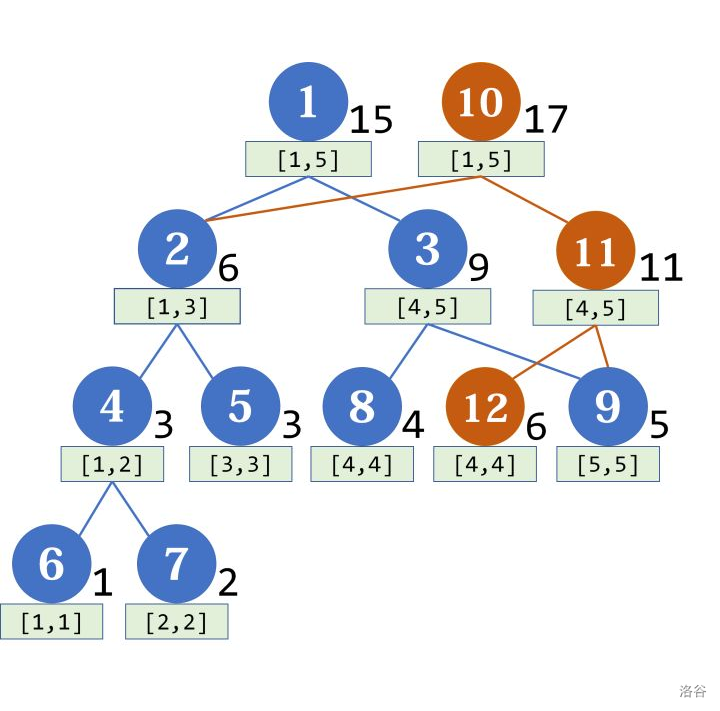
这样就完成了单点修改这样就完成了单点修改。
事实上我们没有修改任何东西,我们保留了原来的版本,并新增了一个修改后的版本。这样既节省了时间,也节省了空间,这就是主席树
方法总结如下:
1.将原始数组复制一份,然后排序好,然后去掉多余的数,即将数据离散化。推荐使用\(C++\)的\(STL\)中的\(unique\)函数;
2.以离散化数组为基础,建一个全0的线段树,称作基础主席树;
3.对原数据中每一个\([1,i]\)区间统计,有序地插入新节点(题目中i每增加1就会多一个数,仅需对主席树对应的节点增加1即可);
4.对于查询\([1,r]\)中第\(k\)小值的操作,找到\([1,r]\)对应的根节点,我们按照线段树的方法操作即可(这个根节点及其子孙构成的必定是一颗线段树)。
下面放一个经典例题:主席树求区间\([l,r]\)第k小的值
【模板】可持久化线段树 2直达
题目背景
这是个非常经典的可持久化权值线段树入门题——静态区间第 \(k\) 小。(我使用vectoe写的,我觉得vector比较好用)
数据已经过加强,请使用可持久化权值线段树。同时请注意常数优化。
题目描述
如题,给定 \(n\) 个整数构成的序列 \(a\),将对于指定的闭区间 \([l, r]\) 查询其区间内的第 \(k\) 小值。
输入格式
第一行包含两个整数,分别表示序列的长度 \(n\) 和查询的个数 \(m\)。
第二行包含 \(n\) 个整数,第 \(i\) 个整数表示序列的第 \(i\) 个元素 \(a_i\)。
接下来 \(m\) 行每行包含三个整数 $ l, r, k$ , 表示查询区间 \([l, r]\) 内的第 \(k\) 小值。
输出格式
对于每次询问,输出一行一个整数表示答案。
样例 #1
样例输入 #1
5 5
25957 6405 15770 26287 26465
2 2 1
3 4 1
4 5 1
1 2 2
4 4 1
样例输出 #1
6405
15770
26287
25957
26287
提示
样例 1 解释
\(n=5\),数列长度为 \(5\),数列从第一项开始依次为\(\{25957, 6405, 15770, 26287, 26465\}\)。
- 第一次查询为 \([2, 2]\) 区间内的第一小值,即为 \(6405\)。
- 第二次查询为 \([3, 4]\) 区间内的第一小值,即为 \(15770\)。
- 第三次查询为 \([4, 5]\) 区间内的第一小值,即为 \(26287\)。
- 第四次查询为 \([1, 2]\) 区间内的第二小值,即为 \(25957\)。
- 第五次查询为 \([4, 4]\) 区间内的第一小值,即为 \(26287\)。
数据规模与约定
- 对于 \(20\%\) 的数据,满足 \(1 \leq n,m \leq 10\)。
- 对于 \(50\%\) 的数据,满足 \(1 \leq n,m \leq 10^3\)。
- 对于 \(80\%\) 的数据,满足 \(1 \leq n,m \leq 10^5\)。
- 对于 \(100\%\) 的数据,满足 \(1 \leq n,m \leq 2\times 10^5\),\(|a_i| \leq 10^9\),\(1 \leq l \leq r \leq n\),\(1 \leq k \leq r - l + 1\)。
#include<cstdio>
#include<algorithm>
#include<vector>
const int N=2e5+5;
using namespace std;
vector<int>G;
int a[N],root[N];
int n,m,l,r,k,cnt;
struct node{int l,r,sum;}tree[N*40];
int getid(int x){return lower_bound(G.begin(),G.end(),x) - G.begin() + 1;}
void insert(int l,int r,int pre,int &pos,int p)
{
tree[++cnt]=tree[pre];
tree[pos=cnt].sum++;
if(l==r) return ;
int mid=l+r>>1;
if(p<=mid) insert(l,mid,tree[pre].l,tree[pos].l,p);
else insert(mid+1,r,tree[pre].r,tree[pos].r,p);
}
int query(int l,int r,int L,int R,int k)
{
if(l==r) return l;
int p=tree[tree[R].l].sum - tree[tree[L].l].sum;
int mid=l+r>>1;
if(k<=p) return query(l,mid,tree[L].l,tree[R].l,k);
else return query(mid+1,r,tree[L].r,tree[R].r,k-p);
}
signed main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),G.push_back(a[i]);
sort(G.begin(),G.end());
G.erase(unique(G.begin(),G.end()),G.end());
for(int i=1;i<=n;i++)
{
int p=getid(a[i]);
insert(1,n,root[i-1],root[i],p);
}
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&l,&r,&k);
printf("%d\n",G[query(1,n,root[l-1],root[r],k) - 1 ] );
}
return 0;
}


