P2805 [NOI2009]植物大战僵尸

题目链接

题目分析

这道题目让我暂时一段时间内不想玩植物大战僵尸了

其实我们只要搞清楚之后 建个模 就会发现 这其实是一道最大权闭合子图问题

只有消灭了所有护着这株植物的所有植物 才可以消灭这株植物 也就意味着我们要消灭这株植物 就不可以不管护着ta的植物

符合闭合子图的概念

首先 这株植物在哪些植物的攻击范围之内 就意味着哪些植物护着ta

其次 这株植物右边的植物必须被僵尸吃掉 才可被消灭 所以这株植物右边的植物也护着ta

所以我们建图 然后跑最小割就可以......了？

如果出现下面的场景呢

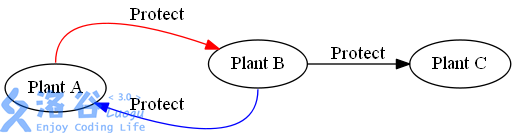
圈中的植物 无法被消灭 被圈中的植物保护的植物 同样无法被消灭

所以 我们先由保护的植物向被保护的植物连边

从入度为零也就是没有被保护的植物 开始进行拓扑 然后找出所有的可以被逐个击破的植物

接下来我们建图的时候只需要考虑 这些植物的点是否合法就可以了

CODE：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<cmath>
#include<queue>
#define N 500080
#define inf 999999999999999LL
#define ll long long
using namespace std;
template<typename T>void read(T &_)
{
	T __=0,___=1;char ____=getchar();
	while(!isdigit(____)) {if(____=='-') ___=0;____=getchar();}
	while(isdigit(____)) {__=(__<<1)+(__<<3)+____-'0';____=getchar();}
	_=___ ? __:-__;
}
int n,m,S,T,tot=1;
int to[N],nex[N],head[N],in[N],cur[N],dep[N];
ll ans,w[N];
bool okay[N];
vector<int> link[N];
queue<int> que;
struct Node
{
	int num;ll val;
	pair<int,int> have[100];
}pro[22][32];
int getid(int x,int y)
{return (x-1)*m+y;}
void add(int x,int y,ll z)
{to[++tot]=y;nex[tot]=head[x];head[x]=tot;w[tot]=z;
swap(x,y);to[++tot]=y;nex[tot]=head[x];head[x]=tot;w[tot]=0;}
void topsort()
{
	for(int i=1;i<=n*m;++i) if(!in[i]) que.push(i),okay[i]=1;
	for(;!que.empty();)
	{
		int now=que.front();que.pop();
		for(int i=0;i<(int)link[now].size();++i)
		{
			int v=link[now][i];
			in[v]--;
			if(!in[v]) que.push(v),okay[v]=1;
		}
	}
	
}
bool bfs()
{
	for(int i=1;i<=T;++i) dep[i]=0;
	dep[S]=1;que.push(S);
	for(;!que.empty();)
	{
		int u=que.front();que.pop();
		for(int i=head[u];i;i=nex[i])
		{
			int v=to[i];
			if(w[i]>0&&dep[v]==0)
			{
				dep[v]=dep[u]+1;
				que.push(v);
			}
		}
	}
	return dep[T]!=0;
}
ll dfs(int now,ll res)
{
	if(now==T||!res) return res;
	for(int &i=cur[now];i;i=nex[i])
	{
		int v=to[i];
		if(w[i]>0&&dep[v]==dep[now]+1)
		{
			ll have=dfs(v,min(res,w[i]));
			if(have>0)
			{
				w[i]-=have;
				w[i^1]+=have;
				return have;
			}
		}
	}
	return 0;
}
void Dinic()
{
	while(bfs())
	{
		for(int i=1;i<=T;++i) cur[i]=head[i];
		ans-=dfs(S,inf);
	}
}
int main()
{
	read(n);read(m);S=n*m+1;T=n*m+2;
	if(n==18&&m==30) {puts("55983");return 0;}
	for(int i=1;i<=n;++i)
	 for(int j=1;j<=m;++j)
	 {
	 	read(pro[i][j].val);
	 	read(pro[i][j].num);
	 	for(int k=1,x,y;k<=pro[i][j].num;++k)
	 	{
	 		read(x);read(y);++x;++y;
	 		pro[i][j].have[k]=make_pair(x,y);
		}
	 }
       //我们统计入度
	for(int i=1;i<=n;++i)
	 for(int j=1;j<=m;++j)
	 {
	 	if(j<m) link[getid(i,j+1)].push_back(getid(i,j)),in[getid(i,j)]++;
	 	for(int k=1;k<=pro[i][j].num;++k)
	 	{
	 		link[getid(i,j)].push_back(getid(pro[i][j].have[k].first,pro[i][j].have[k].second));
	 		in[getid(pro[i][j].have[k].first,pro[i][j].have[k].second)]++;
		}
	 }
	topsort(); //我们跑拓扑排序寻找合法的植物点
	for(int i=1;i<=n;++i)
	 for(int j=1;j<=m;++j)
	 {
	 	if(j<m) add(getid(i,j),getid(i,j+1),inf);
	 	for(int k=1;k<=pro[i][j].num;++k)
	 	add(getid(pro[i][j].have[k].first,pro[i][j].have[k].second),getid(i,j),inf);
	 }
	for(int i=1;i<=n;++i)
	 for(int j=1;j<=m;++j)
	  {
	  	if(!okay[getid(i,j)]) continue;
		if(pro[i][j].val>0) add(S,getid(i,j),pro[i][j].val),ans+=pro[i][j].val;
	    else add(getid(i,j),T,-pro[i][j].val);
	  }
	Dinic(); //我们愉快的跑最小割  
	printf("%lld\n",ans);
	return 0;
}