学习笔记 无向图删边游戏
无向图删边游戏
树上删边游戏
在某一棵树上删除一条边,同时删去所有在删除后不再与根相连的部分
双方轮流操作,无法再进行删除者判定为失败
一个游戏中有多棵树,
我们把TA们的根都放在地板上,方便之后的处理 、
轮到谁是无法删的一方获胜
树上问题@leige
竹子
为了方便 我们先引入竹子(也就是链)
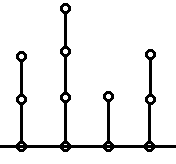
Nim游戏变形
SG[ x ]=x
克朗原理
对于树上摸一个点 TA的分支可以转化为以这个点为根的一个竹子
竹子长度就是 TA各个分支的边的数量的疑惑和
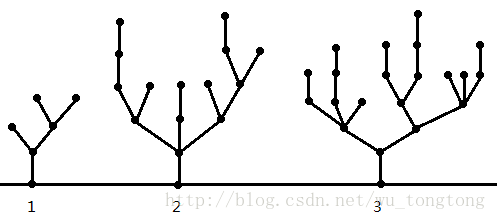
1号树 最后是一条边的竹子 SG1=1
2号树 SG2=8
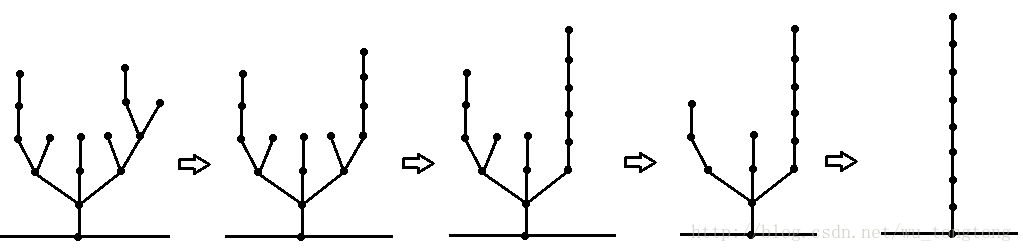
3号树 SG3=4

克朗定理的相关证明【我是证明】
无向图上删边游戏
这里有一个无向图
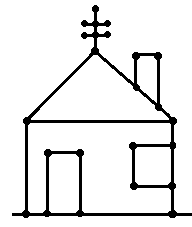
这里根等同于地板
一脸大雾~~~~
是不是有什么东西可以帮我们把TA氪成一个树形结构
费森定理
环上的点是可以融合的 并且不改变图的SG值
从栗子入手
门独立于大框 从门开始
地板上的两个点可以视为一个 因为地板本身就是一个大点
这样的话这扇门就成为了一个三角形 (也就是一个有三个点的环)
费森原理指出 我们可以把换上一个点等价成一个自环 而这个环又可以成为一条边

一般来讲
一个带奇数边的环就是一个只有一个端点的边
一个带偶数边的环就是一个点
那么这样的话就可以所缩点了
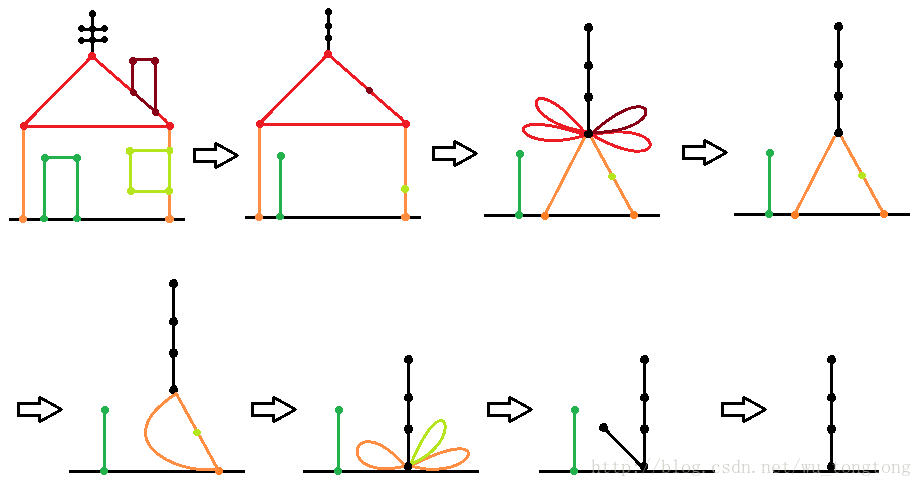
最好还是感性理解一下
结论
对于无向图 我们先利用费森原理 将其转化为一棵树
然后 对于一棵树
树上节点的SG值就是
TA的所有子节点的SG值+1之后的异或和
具体操作的话
我们可以使用
Tarjan 缩点 dfs 构造 仙人掌布拉布拉滴
例题




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 深入理解 Mybatis 分库分表执行原理
· 如何打造一个高并发系统?
· .NET Core GC压缩(compact_phase)底层原理浅谈
· 现代计算机视觉入门之:什么是图片特征编码
· .NET 9 new features-C#13新的锁类型和语义
· Sdcb Chats 技术博客:数据库 ID 选型的曲折之路 - 从 Guid 到自增 ID,再到
· 语音处理 开源项目 EchoSharp
· 《HelloGitHub》第 106 期
· Spring AI + Ollama 实现 deepseek-r1 的API服务和调用
· 使用 Dify + LLM 构建精确任务处理应用