联赛模拟26_Lesson5！

考虑用最长路径树解决

先正反拓扑

正着跑出最长路径树，\(dis\)也就是树中的\(dep\)

反着跑出每个点到终点的最大距离rdis.

删去一个点x剩下的最长路径的终点有两种情况，在x的子树中和不在x的子树中。

• 不在子树中的

直接用dfn序，区间维护最大的dis即可

• 在子树中的

对于一条非树边\((i,j)\),j在x子树中而i不在，对删去x后最长路径

贡献为\(dis[i]+rdis[y]+1\),我们将这样的边从大到小排序后，对于满足\((i,j)\)中j在x子树中而i不在的x，更新一遍即可,

用个并查集维护，\(fa[x]\)表示x及其父亲中第一个未更新的点

例如:非树边\((i,j)\)，他们对会对\(j\)到\(lca(i,j)\)之间的点产生\(dis[i]+rdis[j]+1\) 的贡献，(如下图橙色的点)

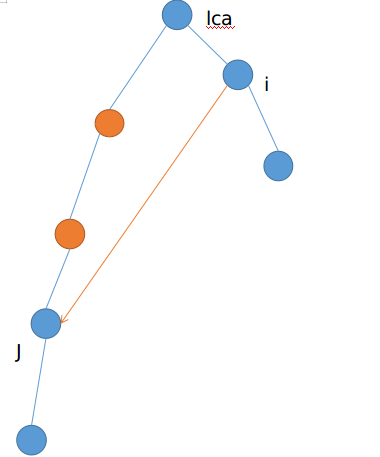
这样就求出了删去x后的图中的最长路径\(Ans[x]\),然后取\(Ans\)最小且尽量\(x\)编号最小就可以

Code

#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <queue>
#include <vector>
#define rint register int
using namespace std;

const int maxn=1e5+5;
const int maxm=5e5+5;
const int INF=0x3f3f3f3f;
int n,m,cnt[3],head[3][maxn];
int dis[maxn],rdis[maxn];
int zd[maxn],fd[maxn];
int in_edge[maxn];
int ans,del_node;
int Ans[maxn];
int fa[maxn],siz[maxn],son[maxn],top[maxn];
bool bel_tree[maxm+maxn];

struct Edge{
	int from,to,next;
}e[3][maxm+maxn];

int tot,F[maxn];
struct P{
	int x;
	int y;
	int val;
	bool operator < (const P &B)const{
		return val>B.val;
	}
}pa[maxm+maxn];

int dfn[maxn][2],Time,mx[maxn][20],lg[maxn];

char buf[1<<20],*p1,*p2;
#define gc() (p1==p2?(p2=buf+fread(p1=buf,1,1<<20,stdin),p1==p2?EOF:*p1++):*p1++)
#define read() ({\
	rint x=0;register bool f=0;register char ch=gc();\
	while(ch<'0'||ch>'9') f|=ch=='-',ch=gc();\
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch&15),ch=gc();\
	f?-x:x;\
})

void Init(){
	memset(fa,0,sizeof fa);
	memset(son,0,sizeof son);
	memset(cnt,0,sizeof cnt);
	memset(bel_tree,0,sizeof bel_tree);
	for(rint i=0;i<=n+2;++i){
		in_edge[i]=0;
		zd[i]=0,fd[i]=0;
		dis[i]=0,rdis[i]=0;
		head[0][i]=0,head[1][i]=0,head[2][i]=0;
	}
	ans=INF,tot=0;
	Time=0;
}

void Aedge(rint x,rint y,rint id){
	e[id][++cnt[id]].to=y;
	e[id][cnt[id]].next=head[id][x];
	e[id][cnt[id]].from=x;
	head[id][x]=cnt[id];
}

queue < int > q;

void cal_max1(){
	q.push(n+1);
	while(!q.empty()){
		rint x=q.front();
		q.pop();
		for(rint i=head[0][x];i;i=e[0][i].next){
			const rint y=e[0][i].to;
			if(dis[y]<dis[x]+1){
				dis[y]=dis[x]+1;
				in_edge[y]=i;
			}
			if(--zd[y]==0) q.push(y);
		}
	}
}

void cal_max2(){
	q.push(n+2);
	while(!q.empty()){
		rint x=q.front();
		q.pop();
		for(rint i=head[1][x];i;i=e[1][i].next){
			const rint y=e[1][i].to,w=rdis[x]+1;
			rdis[y] = rdis[y]<w ? w : rdis[y];
			if(--fd[y]==0) q.push(y);
		}
	}
}


void dfs1(rint x,rint prt){
	fa[x]=prt,siz[x]=1;
	dfn[x][0]=++Time;
	for(rint i=head[2][x];i;i=e[2][i].next){
		const rint y=e[2][i].to;
		if(y==prt) continue;
		dfs1(y,x);
		siz[x]+=siz[y];
		if(!son[x]||siz[y]>siz[son[x]]) son[x]=y;
	}
	dfn[x][1]=Time;
}

void dfs2(int x,int tp){
	top[x]=tp;
	if(son[x]) dfs2(son[x],tp);
	for(int i=head[2][x];i;i=e[2][i].next){
		const rint y=e[2][i].to;
		if(y!=son[x]&&y!=fa[x]) dfs2(y,y);
	}
}

int lca(rint x,rint y){
	rint tmp;
	while(top[x]!=top[y]){
		if(dis[top[x]]<dis[top[y]]){ tmp=x;x=y;y=tmp; }
		x=fa[top[x]];
	}
	return dis[x]<dis[y]?x:y;
}

int find(rint x){
	return F[x]==x?x:F[x]=find(F[x]);
}

int query(rint l,rint r){
	if(l>r) return 0;
	const rint d=lg[r-l+1];
	return max(mx[l][d],mx[r+1-(1<<d)][d]);
}

void pre(){
	for(rint i=1;i<=Time;++i) mx[dfn[i][0]][0]=dis[i];
	for(rint j=1;j<=lg[Time];++j){
		for(rint i=1;i+(1<<j)-1<=Time;++i){
			mx[i][j]=max(mx[i][j-1],mx[i+(1<<(j-1))][j-1]);
		}
	}
	for(rint i=1;i<=Time;++i) Ans[i]=max(query(1,dfn[i][0]-1),query(dfn[i][1]+1,Time));
}

int main(){
	freopen("johnny.in","r",stdin);
	freopen("johnny.out","w",stdout);
	rint cs=read();
	for(rint i=2;i<=100002;++i) lg[i]=lg[i/2]+1;
	while(cs--){
		Init();
		n=read(),m=read();
		for(rint i=1;i<=m;++i){
			const rint x=read(),y=read();
			Aedge(x,y,0),Aedge(y,x,1);
			zd[y]++,fd[x]++;
		}
		for(rint i=1;i<=n;++i){
			Aedge(n+1,i,0),Aedge(n+2,i,1);
			zd[i]++,fd[i]++;
		}
		cal_max1();
		cal_max2();
		for(rint i=0;i<=n+2;++i) dis[i]--,rdis[i]--;
		for(rint i=1;i<=n;++i){
			const rint x=e[0][in_edge[i]].from,y=i;
			bel_tree[in_edge[i]]=1;
			Aedge(x,y,2),Aedge(y,x,2);
		}
		dfs1(n+1,0),dfs2(n+1,n+1);
		pre();
		for(rint i=1;i<=cnt[0];++i){
			if(bel_tree[i]) continue;
			const rint x=e[0][i].from,y=e[0][i].to;
			pa[++tot]=(P){x,y,dis[x]+rdis[y]+1};
		}
		sort(pa+1,pa+1+tot);
		for(rint i=1;i<=n+2;++i) F[i]=i;
		for(rint i=1;i<=tot;++i){
			rint x=pa[i].x;
			rint y=pa[i].y;
			const rint lc=lca(x,y);
			const rint v=pa[i].val;
			y=find(fa[y]);
			while(dis[y]>dis[lc]){
				Ans[y]=max(Ans[y],v);
				F[y]=find(fa[y]);
				y=F[y];
			}
		}
		
		for(rint i=1;i<=n;++i) if(Ans[i]<ans||(Ans[i]==ans&&i<del_node)) ans=Ans[i],del_node=i;
		printf("%d %d\n",del_node,ans);
	}
	return 0;
}