bzoj3162 独钓寒江雪 树Hash 树dp 组合数学

链接：http://www.lydsy.com/JudgeOnline/problem.php?id=3162

题意：给出一棵无根树，求出本质不同独立集数目。

这道题真是一道好题……无限$orz$ $VFleaKing$……对着题解看了半天才看明白明明是你太蒻了……

好了不废话直接切入正题。首先我们需要找出一个方式使得所有的同构树形态都一样，怎么办呢，找到这个树的中心，以这个中心为根重新搞。

但是怎么搞出中心呢……首先，中心一定在整棵树最长的链上。那么我们先随意以一个点为起点广搜一次找到最远点，然后以这个点为起点再广搜一次，这两个最远的点就是树上最远点对。

然后我们就一点一点往回缩……缩到中点就是中心……但是可能有一个问题……就是这个中点可能在边上……这时候我们就需要接出一个虚拟节点做根……

然后，我们就要考虑求解了。如果说只求独立集数目那很简单树形$DP$即可……然而这个题目还有一个条件：同构树算同一种……因此我们还要判一下树同构……所以我们还需要判同构……于是我又现学了树$Hash$……

然后我们可以发现，本质不同的方案数就有$C(k,p+k-1)$种……

然后儿子列表就可以改变……变为同一结构出现了多少次……

于是我们可以把正常的独立集公式变一下：

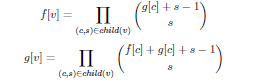
（$f[]$表示选这个节点，$g[]$表示不选这个节点）

二次项系数直接$C(m,n)$就好了……

接下来分类讨论……有中点时，方案数为$f[root]+g[root]$……没有时，由于两个端点不能同时选中，所以还需要继续分类讨论……直接上代码吧……

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int maxn=500005,mod=(int)1e9+7,mod2=(int)1e9+9,inf=0x3f3f3f3f;
struct node
{
    int to,next;
}edge[maxn<<1];
int head[maxn],tot=-1;
void addedge(int u,int v)
{
    edge[++tot]=(node){v,head[u]};head[u]=tot;
}
int n,dis[maxn],from[maxn];
int q[maxn],h,t;
int bfs(int x)
{
    static bool vis[maxn];fill(vis,vis+n+1,0);fill(dis,dis+n+1,inf);h=t=0;
    vis[x]=1,dis[x]=0,q[++t]=x;
    while(h<t)
    {
        int now=q[++h];
        for(int i=head[now];i!=-1;i=edge[i].next)
        {
            int v=edge[i].to;
            if(!vis[v])dis[v]=dis[now]+1,q[++t]=v,vis[v]=1,from[v]=i;
        }
    }
    for(int i=1;i<=n;i++)
        if(dis[i]>dis[x])x=i;
    return x;
}
inline long long qpow(long long x,int tim)
{
    long long tmp=1;
    for(;tim;tim>>=1,x=x*x%mod)
        if(tim&1)tmp=tmp*x%mod;
    return tmp;
}
long long inv[maxn];
void pre()
{
    inv[1]=1;
    for(int i=2;i<=n;i++)inv[i]=(mod-inv[mod%i])*(mod/i)%mod;
}
inline long long C(long long x,long long y)
{
    if(x<0)x+=mod;if(x>=mod)x-=mod;long long ans=1;
    for(int i=1;i<=y;i++)ans=(ans*(x+1-i))%mod,ans=(ans*inv[i])%mod;
    return ans;
}
int root,son[maxn],cp,size[maxn];long long Has[maxn];
inline bool cmp(int x,int y)
{
    return Has[x]<Has[y];
}
inline void getson(int now)
{
    cp=0;
    for(int i=head[now];i!=-1;i=edge[i].next)
    {
        int v=edge[i].to;
        if(dis[v]==dis[now]+1)son[++cp]=v;
    }
    sort(son+1,son+cp+1,cmp);
}
long long Gethash(int now)
{
    getson(now);long long ans=1;
    for(int i=1;i<=cp;i++)ans=(ans+qpow(2,Has[son[i]]))%mod,ans=ans*Has[son[i]]%mod;
    return ans;
}
void Pre()
{
    for(int i=t;i>=1;i--)
    {
        int j=i;
        while(i>1&&dis[q[i]]==dis[q[i-1]])i--;
        for(int k=i;k<=j;k++)Has[q[k]]=Gethash(q[k]);
    }
}
long long f[maxn],g[maxn];
void solve()
{
    for(int i=t;i;i--)
    {
        int now=q[i];f[now]=g[now]=1;getson(now);size[now]=1;
        for(int j=1;j<=cp;j++)size[now]+=size[son[j]];
        for(int j=1;j<=cp;j++)
        {
            int k=j;
            while(j<cp&&Has[son[j+1]]==Has[son[j]])j++;
            f[now]=(f[now]*C(g[son[j]]+j-k,j-k+1))%mod,g[now]=(g[now]*C(f[son[j]]+g[son[j]]+j-k,j-k+1))%mod;
        }
    }
}
int haha()
{
    scanf("%d",&n);memset(head,-1,sizeof(head));
    for(int i=1;i<n;i++)
    {
        int x,y;scanf("%d%d",&x,&y);
        addedge(x,y);addedge(y,x);
    }
    int x=bfs(1),y=bfs(x),l=dis[y],pos=y;
    while(dis[pos]>((l>>1)+1))pos=edge[from[pos]^1].to;
    int lpos;
    if(l&1)
    {
        n++;
        lpos=edge[from[pos]^1].to;edge[from[pos]].to=n;edge[from[pos]^1].to=n;addedge(n,pos);addedge(pos,n),addedge(n,lpos);addedge(lpos,n);
        root=n;
    }
    else
    {
        if(n!=1)pos=edge[from[pos]^1].to;
        root=pos;
    }
    bfs(root);pre();Pre();solve();
    if(l&1)
    {
        long long ans=0;
        if(Has[pos]==Has[lpos])ans=(ans+f[pos]*g[pos]%mod),ans=(ans+C(g[pos]+1,2));
        else ans=(ans+f[pos]*g[lpos]%mod),ans=(ans+g[pos]*f[lpos]%mod),ans=(ans+g[pos]*g[lpos]%mod);
        ans%=mod;
        printf("%lld\n",ans);
    }
    else printf("%lld\n",(f[root]+g[root])%mod);
}
int sb=haha();
int main(){;}