bzoj3643 Phi的反函数 数学 搜索

链接：http://www.lydsy.com/JudgeOnline/problem.php?id=3643

题意：已知$x$，求出$phi(n)==x$的最小$n$。

不得不说今天刷了一堆（相对而言）思博大爆搜之后来这么一道相对有思考价值的数学题真是强啊……

首先我们需要记住一个基本事实：在$int$范围内，每个数的同一个质因数不会成为这个数字的$31$次方，一个数存在的不同质因数不会超过$10$个。

理由很简单：首先$int_max==2147483647$，一定没有任何一个质数$31$次方小于这个数；至于第二个嘛……

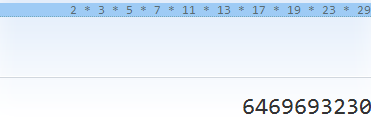
这个东西说明了一切……

了解到这个之后，我们再回顾一下欧拉函数的性质，最重要的一点就在于：它是一个积性函数。于是我们就可以对着一个合数进行三种分类讨论：

1）他自己就是一个质数的欧拉函数，那这个质数一定是他再加$1$；

2）他是几个质数乘积，就递归搞下去。

那么我们就爆搜就可以了。预处理出$sqrt(2147483647)$范围内的质数，然后利用这些扫来扫去，最后特判剩下的是不是质数即可。还有一个优化点：可以证明选择的质数一定是递增的，因此直接递增计算即可。

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<algorithm>
 4 #include<cstring>
 5 #include<cmath>
 6 using namespace std;
 7 const int maxn=50000;
 8 int prime[maxn],tot,n;bool notprime[maxn]={1,1};
 9 void shaisushu()
10 {
11     for(int i=2;i<=50000;i++)
12     {
13         if(!notprime[i])prime[++tot]=i;
14         for(int j=1;j<=tot&&i*prime[j]<=50000;j++)
15         {
16             notprime[i*prime[j]]=1;
17             if(!(i%prime[j]))break;
18         }
19     }
20 }
21 long long pro=1;long long ans=2147483648ll;int mudi;
22 bool isprime(int x)
23 {
24     int mubiao=(int)sqrt(x);
25     for(int i=1;prime[i]<=mubiao;i++)
26         if(!(x%prime[i]))return 0;
27     return 1;
28 }
29 void dfs(int now,int num)
30 {
31     int tpro=pro,tt=now;
32     if(pro>=ans)return;
33     if(now==1){ans=min(ans,pro);return;}
34     if(now>mudi&&isprime(now+1)==1)ans=min(ans,pro*1ll*(now+1));
35     if(prime[num]-1>mudi||now<prime[num]-1)return;
36     for(int i=num;prime[i]<=mudi+1;i++)
37     {
38         if(prime[i]-1>now)return;
39         if(!(now%(prime[i]-1)))
40         {
41             now/=(prime[i]-1);pro*=1ll*prime[i];
42             dfs(now,i+1);
43             while(!(now%prime[i]))
44             {
45                 now/=prime[i],pro*=1ll*prime[i];
46                 dfs(now,i+1);
47             }
48             pro=tpro,now=tt;
49         }
50     }
51 }
52 int haha()
53 {
54     scanf("%d",&n);mudi=(int)sqrt(n);shaisushu();
55     dfs(n,1);
56     if(ans<=0x7fffffff)printf("%lld\n",ans);else puts("-1");
57 }
58 int sb=haha();
59 int main(){;}
bzoj3643

 

posted @ 2017-09-17 21:06  ccc000111  阅读(369)  评论(0)  编辑  收藏  举报