2017/8/12 考试吐槽
2017 8 12 得分:200
我只能说一句话:这才是$NOIP$难度吧……(神$TM$联赛考$FFT$)
A、灌水
题意:$n$根板子长度是$1~n$全排列,找出一种方法,使得板子组成的容器容量恰好为定值。
眼瞪十分钟$+$$coding$ $15$分钟 $+$ $debug$ $5$分钟 $=$ $AC$。
首先我们可以知道,整个容器容量最大的情况就是两根最长的板子夹在两边,中间全是相对较短的板子,这样获得的最大的容量就是\[\frac{(n - 2)(n- 1)}{2 }\]。那么我们就可以知道大于这个的一定不合法。
确定合法之后,我们就可以愉快的贪心了,不断选取当前可抽出的板子中最短的放在左侧并按照递增顺序摆放,避免出现额外容量。合格后直接两个长板放在两边,中间没放过的随意放即可。

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int maxn=(int)1e6+5; 7 int ord[maxn],n;long long x; 8 bool used[maxn]; 9 int haha() 10 { 11 scanf("%d%lld",&n,&x); 12 long long res=1ll*(n-1)*(n-2)/2; 13 if(res<x) 14 { 15 puts("-1"); 16 return 0; 17 } 18 int cur=1,cn=1,nn=1; 19 while(res>x) 20 { 21 long long tmp=res-x; 22 if(tmp>=n-1-cn) 23 { 24 ord[cur]=cn;used[cn]=1; 25 res-=n-1-cn; 26 cn++;cur++; 27 nn=cn; 28 } 29 else 30 for(;nn<n-1;nn++) 31 { 32 if(!used[nn]&&n-1-nn<=tmp) 33 { 34 ord[cur]=nn;used[nn]=1; 35 res-=n-1-nn; 36 cur++;break; 37 } 38 } 39 } 40 ord[cur]=n;ord[n]=n-1;cur++; 41 used[n]=used[n-1]=1; 42 int now=1; 43 while(cur<n) 44 for(;now<=n;now++) 45 if(!used[now]) 46 { 47 used[now]=1;ord[cur]=now; 48 cur++;break; 49 } 50 for(int i=1;i<=n;i++)printf("%d ",ord[i]); 51 } 52 int sb=haha(); 53 int main(){;}
B、序列
题意:求出所有长度为$K$子序列的最大元素之和。
撕烤了十五分钟认为不太可能是第二个思博题,但是又想不到风险系数更低的想法,于是敲了上去。事实证明,正解就是这个……
我们可以发现一个子序列的贡献只与最大元素有关。那么我们就可以只观察最大元素的变化。我们先对序列从小到大排序,对于排序后的序列,从第$K$个开始都是可能的。对于第$i$个元素可以发现它成为最大元素的情况有 $\binom{i-1}{K-1}$种。
直接计算组合数肯定会超时,那么我们考虑前后项之间关系。我们可以看到,前项与后项关系是 $\binom{i-1}{K-1}=\binom{i-2}{K-1}*(i-1)/(i-K)$。那么我们递推计算即可。

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 using namespace std; 6 const int maxn=100005,mod=(int)1e9+7; 7 long long C=1,ans=0; 8 int n,k,a[maxn]; 9 long long qpow(int val,int tim) 10 { 11 long long x=val,tmp=1; 12 for(;tim;tim>>=1,x=x*x%mod) 13 if(tim&1)tmp=tmp*x%mod; 14 return tmp; 15 } 16 int haha() 17 { 18 scanf("%d%d",&n,&k); 19 for(int i=1;i<=n;i++)scanf("%d",&a[i]); 20 sort(a+1,a+n+1); 21 for(int i=k;i<=n;i++) 22 { 23 ans=(ans+C*1ll*a[i]%mod)%mod; 24 C=C*i%mod; 25 C=C*qpow(i-k+1,mod-2)%mod; 26 } 27 printf("%lld\n",ans); 28 } 29 int sb=haha(); 30 int main(){;}
C、修改二叉树
题意:给出一棵二叉树,问最少修改几次可以转化为$BST$。$BST$特点是,左儿子元素$<$父节点元素$<$右儿子元素。
这道题考试时候坑坏我了……刚开始以为这个题是个树归,但是考虑了很久并没有发现什么树形关系……后来在纸上画了画,发现这个东西其实是个什么呢……就像下面这个图:
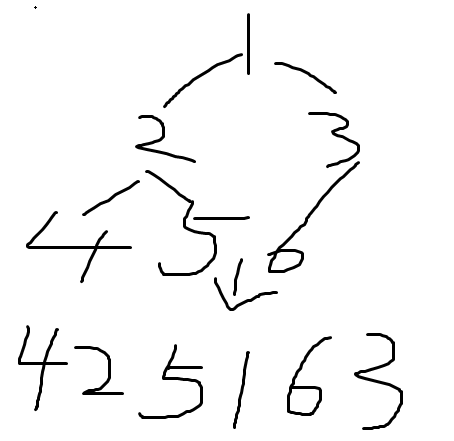
当当当当!就是这个!我意识到$BST$中序遍历之后就可以变成一个序列,这个序列之中最长上升子序列的长度就是不需要修改的长度。于是我就这么敲了一发。
但是交卷后我出了一组数据,发现不太对:
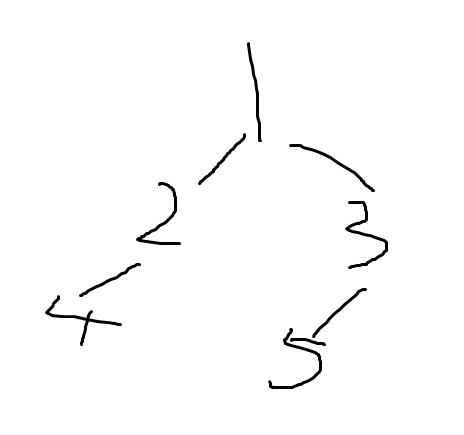
就是这张图。如果说单纯求最长上升子序列长度是$3$,但是这个序列是$2、3、5$,显然中间存在问题,因为$2$、$3$之间存在一个数,这两个数不可能作为最优情况连续出现,正确情况是修改$3$次。但是已经交卷了,再加之脑子很乱,并没有想出怎么解决。
直到看见题解,我的脑子真的是炸裂……每一项中序遍历之后都减去这个数所在位置,问题转化为求出新序列的最长不下降子序列……说不太明白,还是直接代码送上吧……

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 using namespace std; 6 const int maxn=100005; 7 int son[maxn][2],ord[maxn],cnt,n,a[maxn]; 8 long long g[maxn]; 9 void Middle(int root) 10 { 11 if(son[root][0])Middle(son[root][0]); 12 cnt++;ord[cnt]=a[root]-cnt; 13 if(son[root][1])Middle(son[root][1]); 14 } 15 int haha() 16 { 17 scanf("%d",&n); 18 for(int i=1;i<=n;i++) 19 scanf("%d",&a[i]); 20 for(int i=2;i<=n;i++) 21 { 22 int x,y;scanf("%d%d",&x,&y); 23 son[x][y]=i; 24 } 25 Middle(1); 26 for(int i=1;i<=n;i++)g[i]=2147483648ll; 27 int ans=0; 28 for(int i=1;i<=n;i++) 29 { 30 int k=upper_bound(g+1,g+n+1,ord[i])-g; 31 ans=max(ans,k); 32 g[k]=ord[i]; 33 } 34 printf("%d\n",n-ans); 35 } 36 int sb=haha(); 37 int main(){;}



