2017/8/9 考试吐槽
2017 8 9 得分:70
感觉现在自己最弱的地方不是在于思维活性上,而是在于那些本不应该出现在我身上的问题,比如说什么看出正解打不出来啦、打出正解莫名其妙被卡分啦、莫名其妙少些什么导致爆零啦、读不懂题啦、读不懂题啦、读不懂题啦……反正问题太多了……
A、calc
题意:求出所有顺序对的贡献,定义顺序对贡献为这两个数之间比前者大比后者小数的个数。
一眼瞪出这个东西是用求逆序对的方法搞,但是1、这个东西肯定不是归并排序搞得出来的,2、我不会树状数组求逆序对……欢声笑语中打出$GG$……
实际上也就是这么一个东西……维护两个权值树状数组,一个存比这个数小的数之和,另一个存到这里为止的答案。对于每个数动态维护即可。

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int maxn=300005; 7 long long C[maxn],D[maxn],n,a[maxn],Hash[maxn],cnt; 8 long long lowbit(long long x) 9 { 10 return x&(-x); 11 } 12 void add1(int pos,long long val) 13 { 14 for(;pos<=n;pos+=lowbit(pos))C[pos]+=val; 15 } 16 void add2(int pos,long long val) 17 { 18 for(;pos<=n;pos+=lowbit(pos))D[pos]+=val; 19 } 20 int query1(int pos) 21 { 22 int val=0; 23 for(;pos;pos-=lowbit(pos))val+=C[pos]; 24 return val; 25 } 26 int query2(int pos) 27 { 28 int val=0; 29 for(;pos;pos-=lowbit(pos))val+=D[pos]; 30 return val; 31 } 32 int haha() 33 { 34 scanf("%d",&n); 35 for(int i=1;i<=n;i++)scanf("%d",&a[i]),Hash[i]=a[i]; 36 sort(Hash+1,Hash+n+1); 37 cnt=unique(Hash+1,Hash+n+1)-Hash; 38 long long ans=0,x; 39 for(int i=1;i<=n;i++) 40 { 41 a[i]=lower_bound(Hash+1,Hash+cnt+1,a[i])-Hash; 42 x=query1(a[i]-1);add1(a[i],1); 43 ans+=query2(a[i]-1);add2(a[i],x); 44 } 45 printf("%lld\n",ans); 46 } 47 int sb=haha(); 48 int main(){;}
B、beautiful
题意:定义以一个数为这个数所在子序列的中位数的最长子序列长度为这个数的美丽度,求区间最大美丽度。
考试时候看出是个可能的思博题,然而……并不会求区间中位数……再次$GG$……
第二问就是思博的求区间最大值,因此全部问题就变成了如何求出区间中位数。我用了一种在联赛会死的很惨的简单方法:用$stl::set$正面$A$上去。一共进行元素个数轮操作,每一轮先插入一个元素,然后两个一组地插入数据,两个都比当前中位数小迭代器左移,两个都比中位数大迭代器右移,实时更新迭代器所指内容的美丽度,然后乱搞就是了辣鸡评测机不开$O2$吃枣药丸

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<set> 6 using namespace std; 7 const int maxn=2005; 8 struct pii 9 { 10 int pos,val; 11 bool operator<(const pii &b)const 12 { 13 return val<b.val||(val==b.val&&pos<b.pos); 14 } 15 bool operator>(const pii &b)const 16 { 17 return b<*this; 18 } 19 }pos[maxn]; 20 set<pii>s; 21 int mx[12][maxn],n,val[maxn],q; 22 void st_table() 23 { 24 for(int i=1;i<=n;i++)mx[0][i]=val[i]; 25 for(int i=1;(1<<i)<=n;i++) 26 for(int j=1;j+(1<<i)-1<=n;j++) 27 mx[i][j]=max(mx[i-1][j],mx[i-1][j+(1<<(i-1))]); 28 } 29 int get_max(int l,int r) 30 { 31 int k=0; 32 for(;(1<<(k+1))<=r-l+1;k++); 33 return max(mx[k][l],mx[k][r-(1<<k)+1]); 34 } 35 void get() 36 { 37 for(int i=1;i<=n;i++) 38 { 39 s.clear(); 40 s.insert(pos[i]); 41 set<pii>::iterator it=s.begin(); 42 for(int j=i+1;j<n;j+=2) 43 { 44 s.insert(pos[j]),s.insert(pos[j+1]); 45 if(pos[j]<(*it)&&pos[j+1]<(*it))it--; 46 else if(pos[j]>(*it)&&pos[j+1]>(*it))it++; 47 val[(*it).pos]=max(val[(*it).pos],j-i+2); 48 } 49 } 50 } 51 int haha() 52 { 53 //freopen("beautiful10.in","r",stdin); 54 //freopen("beautiful.out","w",stdout); 55 scanf("%d",&n); 56 //cout<<n<<endl; 57 for(int i=1;i<=n;i++) 58 scanf("%d",&pos[i].val),pos[i].pos=i,val[i]=1; 59 get(); 60 st_table(); 61 scanf("%d",&q); 62 for(int i=1;i<=q;i++) 63 { 64 int l,r;scanf("%d%d",&l,&r); 65 printf("%d\n",get_max(l,r)); 66 } 67 } 68 int sb=haha(); 69 int main(){;}
C、permutation
题意乱的很……一个全排列,我们可以发现元素和位置编号成为了循环,定义这个循环中最大元素开头的循环表达方式为标准循环,将每个循环重新按照循环开头元素大小排序,如果顺序与原序列相同则序列合法,求指定合法排列。
论垃圾题面的危害……考试读了半天竟然没有弄清楚它到底想要表达什么……外加这道辣鸡题目吃了屎一样卡空格、回车,于是……日常爆零……
接下来开始%%%$zzh$ $dalao$思路:
第一步:打出一个恶心的表
第二步:贴出恶心的表:
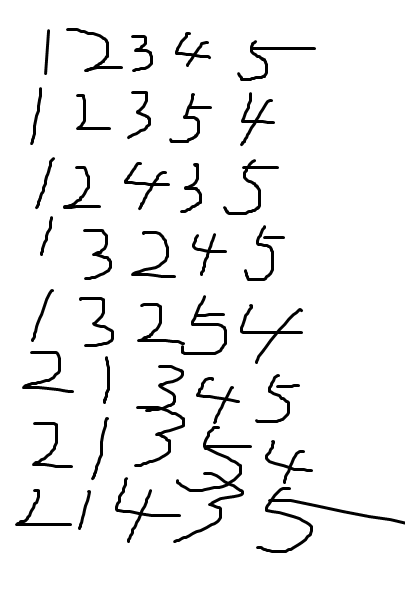
第三步:从这个表中发现肮脏的PY交易正常的数学规律:

可以看出,只可能发生相邻的两个数字交换,且截止到第$i$位完成交换合法的方案数恰好为$Fibonacci$数列第$i+1$项的值。于是我们不加证明地利用这一性质解决问题明明是证不出来好不

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int maxn=55; 7 int n,l[maxn];long long f[maxn],k; 8 int haha() 9 { 10 f[0]=1,f[1]=2; 11 for(int i=2;i<=50;i++)f[i]=f[i-1]+f[i-2]; 12 scanf("%d%lld",&n,&k); 13 while(k>1) 14 { 15 int pos=lower_bound(f+1,f+51,k)-f; 16 k-=f[pos-1];l[n-pos]=n-pos+1,l[n-pos+1]=n-pos; 17 } 18 for(int i=1;i<=n;i++) 19 if(!l[i])l[i]=i; 20 printf("%d",l[1]); 21 for(int i=2;i<=n;i++)printf(" %d",l[i]); 22 } 23 int sb=haha(); 24 int main(){;}


