二叉树
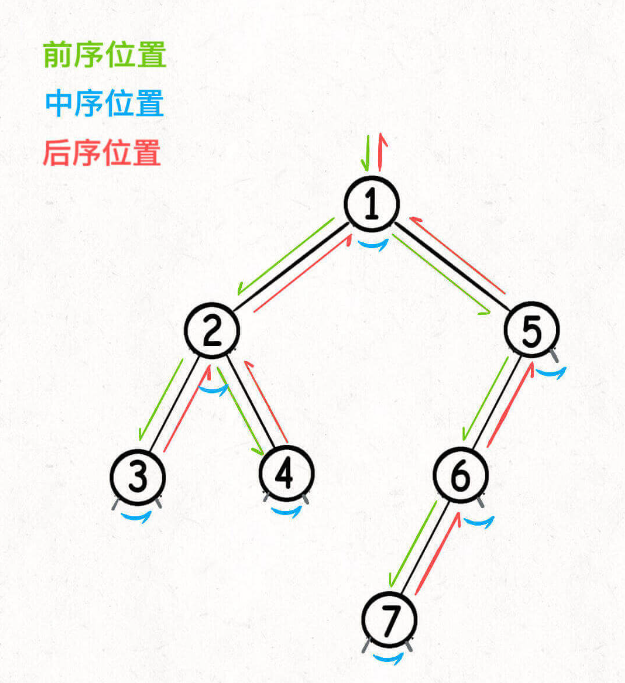
前序位置的代码在刚刚进入一个二叉树节点的时候执行;
后序位置的代码在将要离开一个二叉树节点的时候执行;
中序位置的代码在一个二叉树节点左子树都遍历完,即将开始遍历右子树的时候执行。
void traverse(tree_node root)
{
if(root==null) return;
//前序位置
traverse(root.left);
//中序位置
traverse(root.right);
//后序位置
}
前序位置的代码只能从函数参数中获取父节点传递来的数据,而后序位置的代码不仅可以获取参数数据,还可以获取到子树通过函数返回值传递回来的数据。
题目和子树有关,那大概率要给函数设置合理的定义和返回值,在后序位置写代码了。
两类思路: 遍历一遍二叉树;通过分解问题计算出答案. 分别对应回溯/动态规划
(回溯无返回值, 动态规划有返回值)
二叉树遍历
层序
102. 二叉树的层序遍历
BPS
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vec_all;
//如果为空, 直接返回
if(root == nullptr) return vec_all;
//使用队列保存每层的所有节点,每次把队列里的原先所有节点进行出队列操作,再把每个元素的非空左右子节点进入队列。因此即可得到每层的遍历。
//怎么知道是在这一层呢? 关键是每一次循环都设一个size,没pop一次就size--
queue<TreeNode*> que;
TreeNode* cur = root;
//第一层入队
que.emplace(cur);
//如果队列为空, 就退出循环
while(!que.empty())
{
//如果这一层的元素遍历完了, 就退出循环
int size = que.size();
//存放一层的数据
vector<int> vec;
while(size--)
{
//插入队首元素
vec.emplace_back(que.front()->val);
//如果队首有子节点, 插入到que中
if(que.front()->left!=nullptr) que.emplace(que.front()->left);
if(que.front()->right!=nullptr) que.emplace(que.front()->right);
//删除队首节点
que.pop();
}
//将一层放入vec_all中汇总
vec_all.emplace_back(vec);
}
return vec_all;
}
};
前序
class Solution {
public:
//辅助函数
void pre_order(vector<int>& vec, TreeNode* cur)
{
//递归终止
if(cur == nullptr) return;
//前序遍历就是最先打印出来
vec.push_back(cur->val);
//递归关系
pre_order(vec, cur->left);
// |中序位置|
pre_order(vec, cur->right);
// |后序位置|
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> vec;
TreeNode* cur = root;
pre_order(vec, cur);
return vec;
}
};
迭代
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
if(root==nullptr) return {};
vector<int> res;
stack<TreeNode*> st;
st.push(root);
while(!st.empty())
{
TreeNode* node = st.top();
st.pop();
res.emplace_back(node->val);
if(node->right!=nullptr) st.push(node->right);
if(node->left!=nullptr) st.push(node->left);
}
return res;
}
};
中序
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> st;
while(!st.empty()||root!=nullptr)
{
// 先往左, 遇到就入栈
while(root!=nullptr)
{
st.push(root);
root=root->left;
}
// 拿出中间
root = st.top();
st.pop();
res.emplace_back(root->val);
// 到右边
root = root->right;
}
return res;
}
};
后序
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
if(root==nullptr) return {};
// 前序->中右左->再反过来->后序
vector<int> res;
stack<TreeNode*> st1;
st1.push(root);
while(!st1.empty())
{
TreeNode* node = st1.top();
st1.pop();
res.emplace_back(node->val);
if(node->left!=nullptr) st1.push(node->left); //压栈: 左右 | 读取: 中右左-->reverse->左中右后序
if(node->right!=nullptr) st1.push(node->right);
}
reverse(res.begin(),res.end());
return res;
}
};
几个概念
完美二叉树/完全二叉树/满二叉树
其中, 满二叉树不用做到"除了最后一层, 之前的层都被填充"
底下这个来自SO大佬, 这是我看到的讲得最透彻的图了
Perfect Tree:
x
/ \
/ \
x x
/ \ / \
x x x x
/ \ / \ / \ / \
x x x x x x x x
Complete Tree:
x
/ \
/ \
x x
/ \ / \
x x x x
/ \ /
x x x
Strict/Full Tree:
x
/ \
/ \
x x
/ \
x x
/ \
x x
实践
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
//这是二叉搜索树了, 每一次查找都是"有效的". 最后要么是找到了, 要么是找到null(此时也是root, 合并一下)
if(root == nullptr||root->val == val) return root;
//如果值<该节点的值, 向左搜索, 否则向右搜索
if(val<root->val) return searchBST(root->left,val);
return searchBST(root->right,val);
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//递归问题:返回左右子树的高度差状态, 如果高度差<2则返回最大的那个(子树的深度, 算最深的那个); 如果高度差>=2则返回-1
int recur(TreeNode* cur)
{
//递归终止: 越过子节点 递归回来一个信息: 目前的子节点的深度为0
if(cur == nullptr) return 0;
//左右子树高度left==-1
int left = recur(cur->left);
if(left == -1) return -1; //只要有一个节点的左右子树高度差的绝对值>=2, 这个就是非平衡树, 这个返回-1就病毒一样传播
int right = recur(cur->right);
if(right == -1) return -1;
//递归到最深的时候肯定要越过子节点, 如果目前没有发现是非平衡树, 则返回目前的深度+1
//返回的时候已经把左右节点都递归完了
return abs(left - right)<2 ? max(left,right) + 1:-1;
}
bool isBalanced(TreeNode* root) {
//递归关系 当root左右子树高度差<2 or 左右子树高度差>=2 返回 -1 此子树不是平衡树.
//左右子树的高度怎么得到呢, 根据下一层递归返回的深度
return recur(root)!=-1;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号