从旅行商问题谈状态压缩DP

经典旅行商问题

题目描述

一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短？请输出最短行程。节点个数\(N\)满足\(2 \leq N \leq 20\)，路的长度小于\(1000\)。

分析解答

冷静分析

虽然我没有证明过，但这是一个NP完全问题没错，也就是说不存在已知多项式时间的高效解法，具体可见百度百科的NP完全问题（注意，请最好不要学习模拟退火等算法，因为它无法解决类似的全排列问题）。按我的理解的话，就是其复杂度一般都是指数级别的（不能以偏概全嘛，但是我做的NP完全问题好像都是指数级时间复杂度的）。但是我们对其稍加优化又可以比纯暴力快得多。

例如这个旅行商问题，可能的路线一共有\((n-1)!\)种，如果纯暴力试遍每一种方案，那必然是会超过限定时间的。那么我们就需要一种优化方案了，它就是：状态压缩动态规划。

我们知道，动态规划是根据之前已经计算好的状态推出后面一种状态，这道题亦是如此。也许有人会说，跑一遍最短路不就好了吗？但是最短路不保证走遍每一个点，而即使我们加上了点的计数，那也不能保证从\(A\)上不存在一个环（往回走的环），其节点个数恰好弥补了那些没扫过的节点。而且计数的时候还没到终点的点该如何更新呢？说不定一不小心就更没了，而且如果把每种情况都记录下来，是不亚于枚举的。但是仍有一些弱数据可以被水过去（NOIP），而且这种求最小值的状态压缩题甚至可以被一些优秀的随机化算法（模拟退火）等水过去。不过这些算法最怕的就是求所有状态的题目了，而状态压缩DP就做到了求出所有状态这一点。

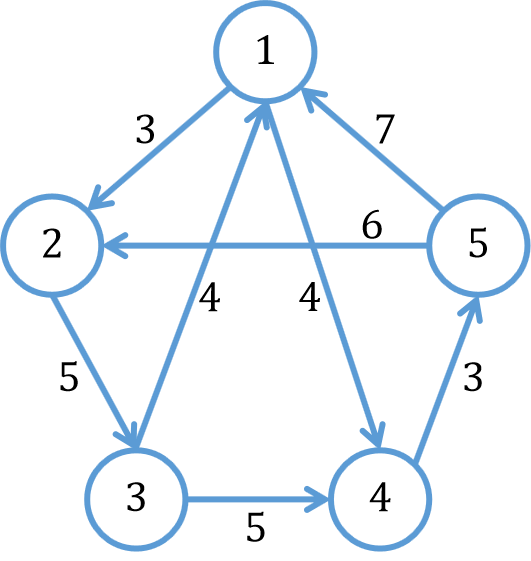
由于博主水平有限，无法带领大家一步一步推理，因此我们就针对递推式进行讲解吧。其递推式为：

\[f[V][0]=0\\ f[S][v]=min\{ f[S\cup \{ u\}][u]+d(v,u)|u\notin S\}\]

其中\(f[S][v]\)表示的是从\(v\)出发访问所有不属于集合\(S\)的顶点，最终回到\(0\)的路径的权重总和的最小值。而集合\(V\)表示为所有城市的集合，不难理解从\(0\)到\(0\)就是路程为\(0\)对吧，并且再将其它所有情况均赋值为无穷大（当然不可能是无穷大啊，找一个达不到的值即可），以防计算不存在的情况。其他的话，递推式已经表达得很明白了，大家也可以举几个例子帮助自己理解（注意，里面有些状态是对答案没用的，大家可以找一找，后面我会提到）。

注意这里出现了集合表示法，但是似乎不好怎么表示这个集合，难道用\(set\)表示吗？那就慢了！别忘了二进制这个好东西。

注意到我们的\(int\)可以表示到\(2^{31}-1\)，然而这里的\(N\)才这么大一点，那么我们就可以在二进制位中逐位保存某个点“存在”和“不存在”的情况。再者，这只需涉及到二进制的位运算，所以整体来说还是很快的。

那么我们现在来为一些稍缺知识的同学补充一些二进制表达集合的方法吧！

二进制表达想必学过一些二进制的人都知道吧，我们需要做的仅仅是摒弃它的十进制的模样（别影响了自己的理性思维）。假设现在有一个集合\(S=\emptyset\)，表示为二进制就是\(00000000\)（假装只有\(8\)位），然后我们往里面加入\(0\)，那么在二进制位的第\(0\)位就要改为\(1\)，也就是\(S=S\cup \{ 0\} =S\vee 2^0=S|1<<0\)。同理，如果往里面加入\(6\)，就是\(S|=1<<6\)（此处计算机表示法均用C++表达）。

如果是判断\(u\)是否存在于集合\(S\)中的话，那么只需要判断\(S\vee 2^u\)（即C++中的\(S\And (1<< u)\)）是否为真就可以了。因为后者仅第\(u\)位是\(1\)，其它部分都是\(0\)，而与的性质是二者都真时才为真，故达到了判断的目的。

于是我们就不难写出程序了。这里以洛谷1171为例。

代码一览

注意，这道题十分卡常！仍然需要优化！但请一步一步看下来，不要急于求成！

下面这段代码仅能得到\(80\)分，但是开\(O2\)可以险过。

#include <cstdio>
#include <algorithm>
#define INF 20000
using namespace std;
int f[(1<<20)][20], d[20][20];
int main()
{
    int i, j, k, n, smax;
    scanf("%d", &n);
    smax = (1 << n) - 1;
    for(i = 0; i < n; i += 1)
        for(j = 0; j < n; j += 1)
            scanf("%d", &d[i][j]);
    for(i = 0; i <= smax; i += 1)
        for(j = 0; j < n; j += 1)
            f[i][j] = INF;
    f[smax][0] = 0;
    for(i = smax-1; i >= 0; i -= 1)
        for(j = 0; j < n; j += 1)
            for(k = 0; k < n; k += 1)
                if(!(i >> k & 1) && j != k)
                    f[i][j] = min(f[i][j], f[1<<k|i][k] + d[j][k]);
    printf("%d", f[0][0]);
    return 0;
}

回过头来我们再看一下这个递推式，实际上还有优化的地步！

\[f[S][v]=min\{ f[S\cup \{ u\}][u]+d(v,u)|u\notin S\} \]

注意到\(min\)中的\(f[S\cup \{ u\}][u]\)保证了\({u}\)必然在集合\(S\cup \{ u\}\)里面，有人可能会说这是废话，但是这说明了在前面的状态中，\(v\)必然在集合\(S\)里面啊！因此对于\(v\)不在集合\(S\)中的情况就不必考虑了。但是，注意当\(S\)为空（程序中变为\(0\)）的时候它就不会继续走答案了，也就是说我们要特殊处理一下这种情况。

于是我们得到了\(90\)分代码。

#include <cstdio>
#define INF 20000
int f[(1<<20)][20], d[20][20];
inline int cmin(int a, int b)
{
    return a < b ? a : b;
}
int main()
{
    int i, j, k, n, smax;
    scanf("%d", &n);
    smax = (1 << n) - 1;
    for(i = 0; i < n; i += 1)
        for(j = 0; j < n; j += 1)
            scanf("%d", &d[i][j]);
    for(i = 0; i <= smax; i += 1)
        for(j = 0; j < n; j += 1)
            f[i][j] = INF;
    f[smax][0] = 0;
    for(i = smax-1; i; i -= 1)
        for(j = 0; j < n; j += 1)
            if(i >> j & 1)/*添加1*/
                for(k = 0; k < n; k += 1)
                    if(!(i >> k & 1))
                        f[i][j] = cmin(f[i][j], f[1<<k|i][k] + d[j][k]);
    int ans = INF;
    for(i = 1; i < n; i += 1)/*添加2*/
        ans = cmin(ans, f[1 << i][i] + d[0][i]);
    printf("%d", ans);
    return 0;
}

那，不开\(O2\)怎么拿\(100\)分呢？答案是舍去多考虑的必然不存在的情况，也就是必然为\(INF\)的情况。

让我们再从头开始看，看那个递推式（稍改）。

\[f[V][0]=0\\ f[S][v]=min\{ f[S\cup \{ u\}][u]+d(v,u)|u\notin S, v\in S\}\]

最开始\(S\)二进制位（位数小于\(N\)）全部是\(1\)的时候，仅\(0\)号点为\(0\)，其它都是\(INF\)。而有些\(INF\)是可以推到底层的！那什么样的情况满足其\(f\)恒为\(INF\)呢？首先注意到\(f[V][x],x\neq 0\)的情况恒为\(INF\)，那这个状态又会推到哪里呢？根据递推式：

\[f[S][v]=min\{ f[S\cup \{ u\}][u]+d(v,u)|u\notin S, v\in S\} \]

我们有：

\[f[S][v]=min\{ f[V][u]+d(v,u)|u\neq \{ 0\} ,u\notin S, v\in S\} \]

容易得到\(f[S][v]\)必然为\(INF\)（因为\(u\)只有一种可能）。

同理，对于递推式：

\[f[S][v]=min\{ f[S\cup \{ u\}][u]+d(v,u)|\{ 0\} \in S ,u\notin S, v\in S\} \]

\(f[S][v]\)必然由一个比当前集合\(S\)（包含元素\(0\)）多一个元素的集合\(S'\)得来，而\(S'\)又以类似方式得来，最终它们共同的来源均为：

\[f[V][u]+d(v,u)|u\neq \{ 0\} ,u\notin S, v\in S \]

故对于任何满足\(\{ 0\} \in S\)的\(f[S][v]\)，它们的值恒为\(INF\)。用二进制表示法来说，只要\(S\And 1\)为真，那么就无需考虑。

那么程序就可以“进化”了，从而拿到\(100\)分！

#include <cstdio>
#define INF 20000
int f[(1<<20)][20], d[20][20];
inline int cmin(int a, int b)
{
    return a < b ? a : b;
}
int main()
{
    int i, j, k, n, smax;
    scanf("%d", &n);
    smax = (1 << n) - 1;
    for(i = 0; i < n; i += 1)
        for(j = 0; j < n; j += 1)
            scanf("%d", &d[i][j]);
    for(i = 0; i <= smax; i += 1)
        for(j = 0; j < n; j += 1)
            f[i][j] = INF;
    f[smax][0] = 0;
    for(i = smax-1; i; i -= 2)
        for(j = 0; j < n; j += 1)
            if(i >> j & 1)
                for(k = 0; k < n; k += 1)
                    if(!(i >> k & 1))
                        f[i][j] = cmin(f[i][j], f[1<<k|i][k] + d[j][k]);
    int ans = INF;
    for(i = 1; i < n; i += 1)
        ans = cmin(ans, f[1 << i][i] + d[0][i]);
    printf("%d", ans);
    return 0;
}

另外，如果各位还追求更高的速度，那么可以将自定义取最小值函数换成标准模板库中的\(min\)函数，然后开一下\(O2\)就能将最慢的900ms+的点提速到200ms+，神奇吧！

注意：以上数据均在洛谷测试，均为C++语言。

轮廓线优化——“棋盘”里的美妙操作

在状态压缩DP里面，我们也经常会碰到一些“棋盘”题。如果直接暴力搜索的话，会产生“状态爆炸”的尴尬局面，于是我们就需要一个美妙的优化方案——轮廓线优化了。

代表题目 [USACO06NOV]Corn Fields

题目大意：有一块\(M\times N\)（\(1\leq M,N\leq 12\)）的长方形牧场，分割的每一块土地都是正方形的（说白了就是棋盘），农夫要在某几格种上牧草或者干脆不种。要求是：不能种在贫瘠的土地上；各个土地上的牧草不能有公共边。土地状况会在输入中给出，求不同的种植方案的个数，答案对\(10^8取模\)。（看你们还怎么用模拟退火）

具体见洛谷1879。

分析解答

冷静分析

也许有人会说：啊！这还怎么用状态压缩啊！\(M\times N\)早就爆炸了啊！（说好的冷静呢）

其实这题有人就这么过了，还写了题解，确实比别的好理解，不过代价就是太慢了。

额哼，不扯了，我们切入正题吧。

其实我们这里没必要搞出这么多状态，我们的方法其实就是逐行递推（逐行动态规划）。转移方程该怎么写呢？也不难，就是根据当前考虑的格子的左边和上面的状态得到当前格的状态。但是要注意不存在的情况及时过滤！于是我们得到递推式：

\[f[0][0]=1\\ f[i][S]+=f[i-1][S]\\ f[i][S\cup u]+=f[i-1][S],u\notin S\]

第一个赋值式表示的是初值（经验所得，下方有答疑）；第二个递推式表示的是这个点不被选取的情况；第三个递推式表示这个点被选取的情况。但是需要注意的是，如果这个点被选了，那么第二第三条递推式都要写上，因为农夫可以选择不种（别被细节坑了哦）！

哦，对了，对于某格上面存在草的情况，递推下来的时候要递推到这格不种草的情况，图示：

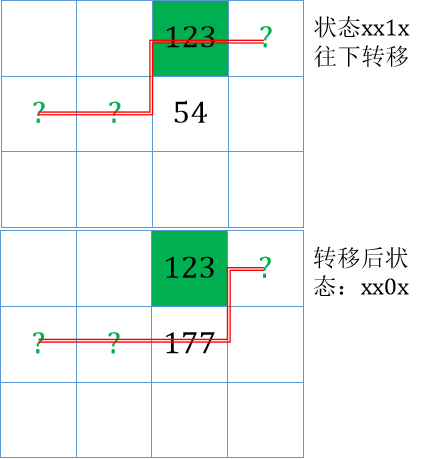
不能种的情况：

1. 上面或左边有草。
2. 该点土地不达标。

但是仍然要转移过来，不然怎么递推到最后一行去统计呢？如果不清楚的话，下文会提到为什么要在最后一行统计。

您可能会问的问题：

1. 为什么\(f[0][0]=1\)啊？（因为第一行也是可以由第\(0\)行推来的，而考虑第一行的时候，第一个位置由于上面没有东西，不会考虑，而它的左边必然是\(0\)的，那么这一个点就可以由转移方程推来）
2. 不用考虑\(S\)中有冲突的情况吗？（不需要，因为冲突情况都是\(0\)的，对答案没有贡献）
3. 不存在的情况有哪些？（比如在第一行的时候考虑上面的情况是不存在的，在第一列的时候考虑左边的情况是不存在的——但这种情况可以人为排除，看我程序就明白了）
4. 可以具体表现（让大家感性理解）一下这个动态规划的形式吗？（如图，包括轮廓线在这里的具体表现）
   
   
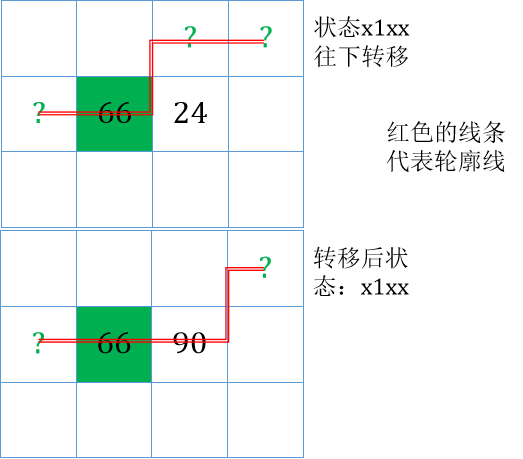
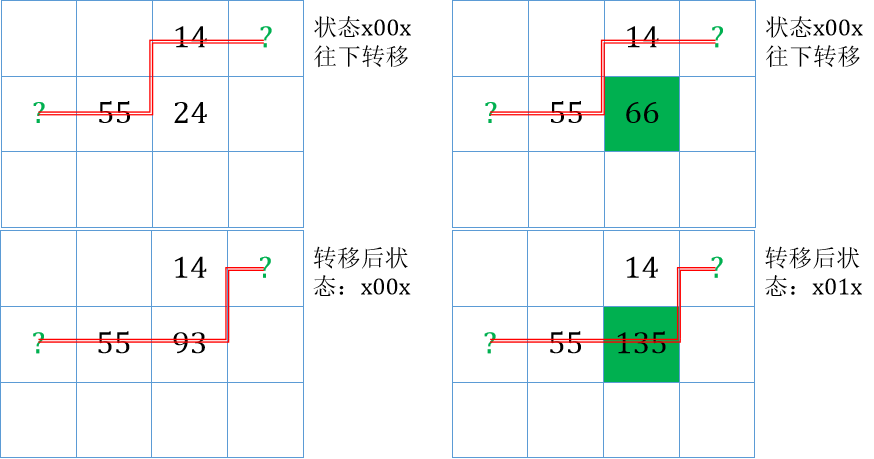
5. 可以证明这些递推式是正确的吗？（很简单，因为每次枚举不同的点，而轮廓线集合是互异的，故可以全部加起来，不过注意最后统计的时候要统计最后一行的所有状态）
6. 为什么选择轮廓线式递推？（老师说这样快一些，未亲测，请各位酌情接受）
7. 如果左、上都有草怎么转移？（虽然图中是在某一格有值的，但是实际操作中，我们可以将其统计到轮廓线上得到一个轮廓线值，那么就算左、上都有草，也只要按照递推式加一下就好了）

还有什么问题也可以通过评论告诉我，或者用洛谷私信也行（洛谷ID：50871）。

为了追求完美，博主用了滚动数组（也就是数组重复利用，不浪费空间）。

下面是满满的注释的代码，博主满满的爱。

代码一览

旧洛谷机子上面必然为0ms的代码，别问我为什么。因为新测评机没有0ms了啊！没赶上啊！不过在洛谷IDE（老测评机）测试全为可种草的土\(12\times 12\)的数据中，跑出来是0ms的。

#include <cstdio>
#define MAXN 15
#define p 100000000
int a[MAXN][MAXN], f[2][1<<MAXN], kmax;
inline void init(int x)//滚动数组初始化函数
{
    for(register int i = 0; i < kmax; i += 1)
        f[x][i] = 0;
}
int main()
{
    int i, j, k, ans = 0;
    int M, N, now = 0, up, left;
    scanf("%d%d", &N, &M);
    kmax = 1 << M;
    for(i = 1; i <= N; i += 1)//正常的行
        for(j = 0; j < M; j += 1)//方便二进制
            scanf("%d", &a[i][j]);
    f[0][0] = 1;
    for(i = 1; i <= N; i += 1)
        for(j = 0; j < M; j += 1)//枚举点
        {
            now ^= 1;//滚动数组走起
            init(now);//注意初始化
            for(k = 0; k < kmax; k += 1)
            {
                up = (1 << j) & k;
                //上面那格和现在这格处于同一列
                //根据轮廓线，这格的左边是同行的
                left = j ? (1 << (j - 1)) & k : 0;
                //看看前面一格有没有草
                //人为排除不存在的情况
                if(i == 1 && up)//人为不好排除就if
                    continue;
                if(up)
                {
                    f[now][k ^ (1 << j)] = (f[now][k ^ (1 << j)] + f[now ^ 1][k]) % p;
                    //注意到同列，因此递推下来的时候就要推到这里不种草的情况
                    continue;
                }
                if(left || !a[i][j])
                {
                    f[now][k] = (f[now][k] + f[now ^ 1][k]) % p;
                    //这里照常推下来就行了
                    continue;
                }
                f[now][k] = (f[now][k] + f[now ^ 1][k]) % p;
                f[now][k | 1 << j] = (f[now][k ^ (1 << j)] + f[now ^ 1][k]) % p;
                //递推式照搬
            }
        }
    for(i = 0; i < kmax; i += 1)
        ans = (ans + f[now][i]) % p;
    //互异，统计，加起来即可，别忘记取模哦
    printf("%d", ans);
    return 0;
}

总结

状态压缩DP虽然说是指数级的DP，但是也涉及到一些细微的优化，甚至可以达到2倍级的优化。所以，在写状态压缩DP的时候也要多想想，多分析分析复杂度。另外，毕克大佬告诉我们不要依赖模拟退火和一些奇技淫巧解这样的题，因为如果出题人出了计数题，那么这些算法就没办法“水”过去了。

还有，这些状态压缩DP只是小部分，后续我可能还会继续更新，比如插头DP等。

参考文献

1. 秋叶拓哉, 岩田阳一, 北川宜稔. 挑战程序设计竞赛（第二版）[M]. 北京:人民邮电出版社, 2013. 191-198
2. 龙_之_谷. 题解 [USACO06NOV]玉米田Corn Fields[EB/OL]. https://www.luogu.org/problemnew/solution/P1879, 2018-08-04

快乐一刻

请你将下列缺陷填好，使其成为完整的旅行商问题的程序：

#include <cstdio>
#define ________ 20000
int _[(1<<20)][20], __[20][20];
inline int __________(int ______, int _______)
{
    return ______ < _______ ? ______ : _______;
}
int main()
{
    int _____, _______, _________, ___________, ____;
    scanf("%d", &___________);
    ____ = (1 << ___________) - 1;
    for(_____ = 0; _____ < ___________; _____ += 1)
        for(_______ = 0; _______ < ___________; _______ += 1)
            scanf("%d", &__[_____][_______]);
    for(_____ = 0; _____ <= ____; _____ += 1)
        for(_______ = 0; _______ < ___________; _______ += 1)
            _[_____][_______] = ________;
    _[____][0] = 0;
    for(_____ = ____-1; _____ ; _____ -= 2)
        for(_______ = 0; _______ < ___________; _______ += 1)
            if(_____ >> _______ & 1)
                for(_________ = 0; _________ < ___________; _________ += 1)
                    if(!(_____ >> _________ & 1))
                        _[_____][_______] = __________(_[_____][_______], _[1<<_________|_____][_________] + __[_______][_________]);
    int ___ = ________;
    for(_____ = 1; _____ < ___________; _____ += 1)
        ___ = __________(___, _[1 << _____][_____] + __[0][_____]);
    printf("%d", ___);
    return 0;
}

别看了，这里没有缺陷，交上去照样AC。

写在最后

推荐大家看看《挑战程序设计竞赛（第二版）》，讲的也很好噢~
感谢参考文献中提到的文献的帮助。
除参考部分外，大多数内容（如常数优化，较为通俗的理解，图片等）均为个人智力成果，如需转载，请注明出处，禁止作商业用途传播。
最后，感谢各位的阅读。