左偏树
抛出问题
有\(n\)个人(一个人可以单独作为一个团体),每个人有一个分数且他们的初始位置是他们的编号,有\(m\)种操作,每次操作可能有两种情况:
- 合并两个团体;
- 找出某个编号的人所在团体的最小分数的人,输出其分数并杀掉他。
\(n\leq 10^6,m\leq 10^5\)。
典例:罗马游戏
解决问题
直接办法
我们发现题目要求中集合了小根堆和并查集两种数据结构,也许我们会想直接合并它们,但是细细想来,小根堆的性质有可能因此破坏。因此咱们有一种直接的方案,就是将其中一个小根堆中的节点(\(n\)个)一个一个地移到另一个小根堆(\(m\)个)中,这样的复杂度就是\(O(n\lg (n+m))\)。
但是注意到数据范围,再加上操作有\(m\)次,所以最坏总复杂度就是\(O(mn\lg (n+m))\),绝对会超时。
新的方法——左偏树
为此,一个新的数据结构就诞生了,它叫"左偏树"。顾名思义,它是一个树状结构,而且是二叉树,而它的节点是向左偏移的(左子树节点可能会多些)。
左偏树的性质
- 左偏树的每个节点都有一个属性(attribution),到最近的叶子节点的距离(我们定义为\(p\)),并且我们认为叶子节点是空节点(它们有\(p=0\)),如图所示;
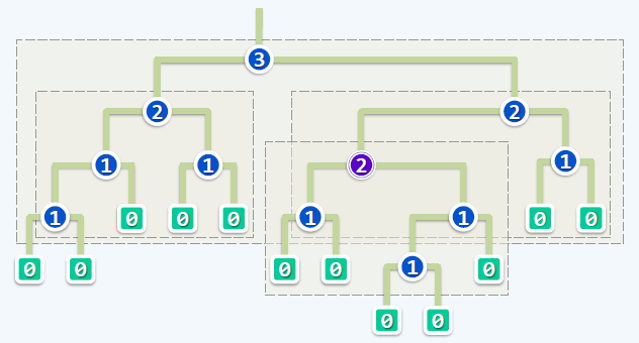
- 左偏树的每个节点的\(p\)恰比其右儿子的\(p\)多\(1\);
- 左偏树的每个节点的左儿子的\(p\)不小于右儿子的\(p\);
- 左偏树满足堆的性质。
左偏树的推论
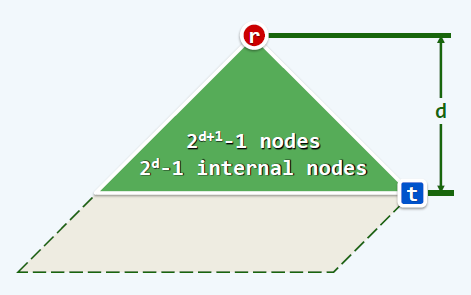
- 左偏树的根节点的\(p\)是\(log\)级别的,也就是说它到最右边节点的距离是\(log\)级别的;
- 左偏树的子树是左偏树;
- 右链长度为\(d\)的左偏树至少包含\(2^{d}-1\)个内部节点,\(d\)实际上就是根的\(p\)值,如图。
左偏树的操作
合并
我们现在假设要合并两个左偏树(小根堆),它们的树根分别为\(a\)和\(b\),如图所示。
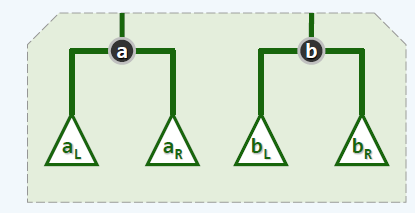
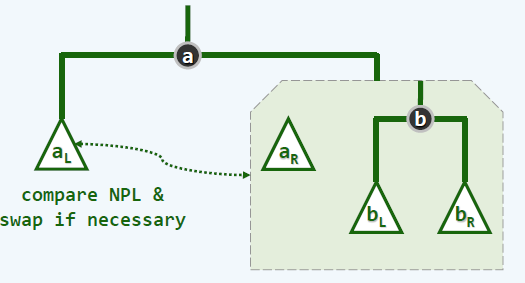
如何合并呢?我们先选出树根(堆顶元素),只需要比较\(a\)和\(b\)即可。假设选出来的是\(a\)(如果选出来是\(b\),那么交换它们即可),注意到左偏树的性质2,我们递归合并\(a\)的右子树\(a_R\)和\(b\)为根的树。这就是左偏树的精华所在。
为什么要这么做?
这样做可以花\(O(\lg n)\)的单次时间复杂度合并两个左偏树,而这恰恰就是利用了它左偏的性质!试想,如果一直这样递归下去,每次选择的都是右子树和另一个树合并,最多也不过就是\(a\)和\(b\)的\(p\)值之和。
但是这还没有结束,在递归合并完毕后要进行维护操作,也就是维护左偏树的性质3。如果\(a\)的左右子树违反了左偏树的性质,交换一下即可。
细节方面:
- 注意底部空节点,作为递归结束标志;
- 记得更新父子关系;
- 最后记得更新\(a\)的\(p\)值。
总结如下:
- 选根,递归合并;
- 维护左偏树性质;
- 注意细节。
插入与删除
插入其实很简单,就是调用一次合并函数,如图。
删除也不难,因为这里删除的是最小元素,也就是树根,我们只需要将其左右子树再合并即可,如图。
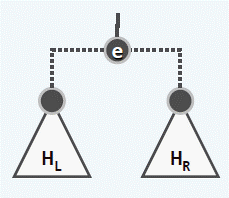
单次复杂度都是\(O(\lg n)\)。
左偏树的实现
左偏树可以用数组实现,也可以用指针实现,但是指针实现在查询方面不太好做,所以一般是用数组实现的。在处理上也有一些小技巧,可能也不算什么,不过大家可以细看一下。这是左偏树的模板,点我去模板题,我的代码如下:
#include <cstdio>
struct TREE
{
int val, lc, rc, npl, fa;
}t[100010];
inline int read()
{
int x = 0;
char ch = getchar();
while(ch < '0' || ch > '9')
ch = getchar();
while(ch >= '0' && ch <= '9')
x = (x<<3) + (x<<1) + (ch^48), ch = getchar();
return x;
}
inline void swap(int &a, int &b)
{
int t = a;
a = b;
b = t;
}
int merge(int a, int b)
{
if(!a) return b;
if(!b) return a;
if(t[a].val > t[b].val || (t[a].val == t[b].val && a > b))
swap(a, b);
int &ar = t[a].rc, &al = t[a].lc;
ar = merge(ar, b);
t[ar].fa = a;
if(t[al].npl < t[ar].npl)
swap(al, ar);
t[a].npl = t[ar].npl + 1;
return a;
}
void del(int a)
{
int al = t[a].lc, ar = t[a].rc;
t[a].val = -1;
t[al].fa = 0;
t[ar].fa = 0;
merge(al, ar);
}
inline int find(int a)
{
while(t[a].fa)
a = t[a].fa;
return a;
}
int main()
{
int n, m;
int x, a, b;
n = read(); m = read();
t[0].val = -1;
for(register int i = 1; i <= n; i += 1)
t[i].val = read();
for(register int i = 0; i < m; i += 1)
{
x = read();
if(x == 1)
{
a = read(); b = read();
if(t[a].val != -1 && t[b].val != -1)//一定要加上去,不然合并就会出问题
{
a = find(a), b = find(b);
if(a != b)//注意判断
merge(a, b);
}
}
else
{
a = read();
if(t[a].val == -1)
printf("-1\n");
else
{
a = find(a);
printf("%d\n", t[a].val);
del(a);
}
}
}
return 0;
}
时间复杂度:\(O(m\lg n)\)。相应的,解决顶上的问题就不难了——其实就是稍微改改就行了。
尾注
不知道是哪个左撇子发明的这个数据结构。。。
左偏树这个数据结构还是非常棒的,这也提醒我们应该学会创造性思维。
- 感谢LMH大佬的帮助;
- 感谢洛谷平台的帮助;
- 感谢那些写题解的大佬的帮助。
写在最后
感谢大家的关注和阅读。
本文章借鉴了少许思路,最后经过本人思考独立撰写此文章,如需转载,请注明出处。


