状压dp个人总结
注意,这里仅进行总结,具体教程请看历史博客~
经典问题重现
问题描述
〖旅行商问题〗一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。应如何选择行进路线,以使总的行程最短?请输出最短行程。节点个数\(N\)满足\(2 \leq N \leq 20\),路的长度小于\(1000\)。
问题思考
这里我们可以采用这样的递推方式(与教程博客不同):假设 \(f[S][u]\) 表示已走过 \(S\) 集合内的点,现在正处于 \(u\) 点。如果可以从 \(u\) 经过一条边到达 \(v\) 点,那么转移方程可以写成:
但是我们显然知道,最后落脚在第一个点的话,前面就都不可以在第一个点落脚,状态减少一半。同时在计算过程中,不存在的转移状态要及时去除,这样也可以给计算时间以极大的缩短(算是卡常)。
代码一览
#include <bits/stdc++.h>
const int INF = 20000;
using namespace std;
int f[(1<<20)+5][20], d[20][20], p[20];
int main()
{
int i, j, k, n, smax;
scanf("%d", &n);
for(i = 0; i <= n; i += 1)
p[i] = 1<<i;
smax = p[n] - 1;
for(i = 0; i < n; i += 1)
for(j = 0; j < n; j += 1)
scanf("%d", &d[i][j]);
for(i = 0; i <= smax; i += 1)
for(j = 0; j < n; j += 1)
f[i][j] = INF;
for(i = 1; i < n; i += 1)
f[p[i]][i] = d[0][i]; //第一个点特别处理
for(i = 2; i <= smax; i += 2) //枚举除到第一个点之外的所有状态进行转移
for(j = 1; j < n; j += 1)
if(i & p[j]) //当前处于的点必须在集合中
for(k = 1; k < n; k += 1)
if(!(i & p[k])) //要去往的点不能在集合内
f[i|p[k]][k] = min(f[i|p[k]][k], f[i][j] + d[j][k]);
for(j = 1; j < n; j += 1)
f[smax][0] = min(f[smax][0], f[smax^1][j] + d[j][0]); //最后回来的点也要特别处理
printf("%d", f[smax][0]);
return 0;
}
经典棋盘问题
问题描述
用 \(1\times 2\) 的骨牌摆满一个 \(8\times 8\) 的棋盘有多少种摆法?
问题思考
这是经典的轮廓线动态规划。我们对轮廓线处在的格子定义两个状态,一个是已经摆好了骨牌,一个是只摆了一半的骨牌。虽然我们知道骨牌是有方向的,但是这里并不需要这么考虑。因为摆了一半说明肯定没摆好,需要对后面的状态进行匹配,摆好了就不需要动了。而这些状态之间又是互不干涉的,所以统计起来是既完全又方便的。那么对于轮廓线上的某一格,它需要转移的有如下几种有效情况:
上方格未匹配
上方格已经被考虑过,所以无法改变它的状态,因此,当前格必须与上方格进行匹配。直接转移即可。
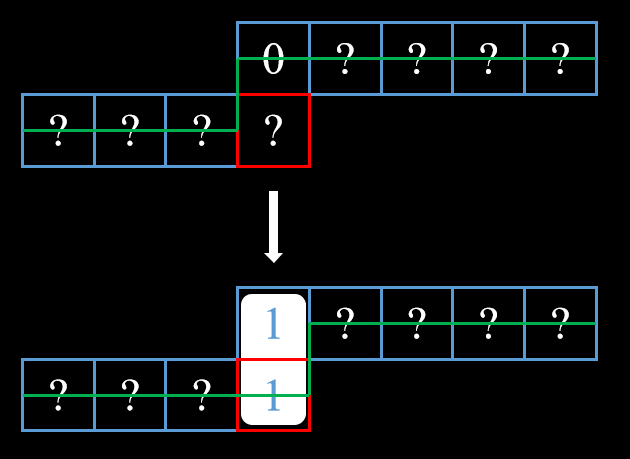
左方格未匹配
这是建立在上方格已匹配的基础上,所以不用考虑上方格。对于左方格可以进行匹配,也可以不去匹配。这两种状态分别进行转移即可。
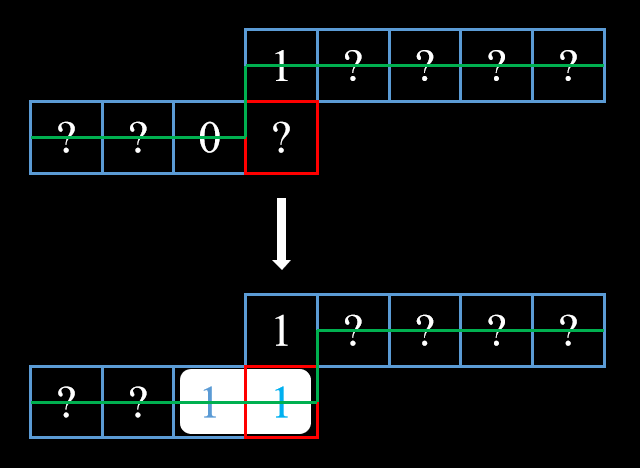
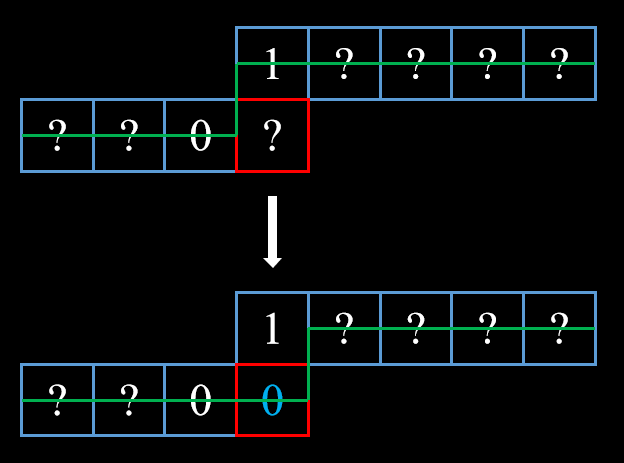
相邻格都已匹配
本格只能处于未匹配状态,直接转移即可。
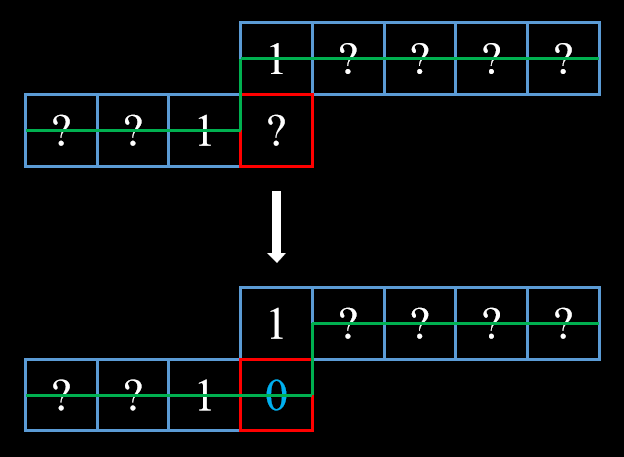
拓展到 \(n\times m\)
这样就是 UVA11270 Tiling Dominoes 这道题了。
代码一览
#include <bits/stdc++.h>
using namespace std;
long long f[2][(1<<10)+5];
int p[11];
int main()
{
int n, m, d, r;
for(register int i = 0; i <= 10; i += 1)
p[i] = 1<<i;
while(~scanf("%d%d", &n, &m))
{
d = 0;
if(n < m)
swap(n, m);
memset(f, 0, sizeof(f));
r = p[m];
f[0][r-1] = 1;
for(register int i = 0; i < n; i += 1)
for(register int j = 0; j < m; j += 1)
{
d ^= 1;
memset(f[d], 0, sizeof(f[d]));
for(register int k = 0; k < r; k += 1)
{
if(i && !(k&p[j])) //上格未匹配
f[d][p[j]|k] += f[d^1][k];
if(k&p[j]) //不论左格何种情况,不去匹配
f[d][p[j]^k] += f[d^1][k];
if(j && !(k&p[j-1]) && k&p[j]) //左格未匹配,与当前格进行匹配
f[d][p[j-1]|k] += f[d^1][k];
}
}
cout << f[d][r-1] << endl;
}
return 0;
}
棋盘间隔问题
基础问题
〖USACO06NOV - Corn Fields〗有一块 \(M\times N\)(\(1\leq M,N\leq 12\))的矩形牧场,分割的每一块土地都是正方形的(说白了就是棋盘),农夫要在某几格种上牧草或者干脆不种。要求是:不能种在贫瘠的土地上;各个土地上的牧草不能有公共边。土地状况会在输入中给出,求不同的种植方案的个数,答案对 \(10^8\) 取模。
这个问题很简单,照猫画虎,照方抓药。轮廓线法转移过程中注意相邻都有草的状态转移过来这边不能有草,如果都没有草,则既可以有草也可以无草。代码在历史博客贴出过,此处略。
〖HDU1565 - 方格取数(1)〗\(N\times N\)(\(1\leq N\leq 20\))方格上有许多非负整数,在方格中取出若干数满足这些数所在的格子两两不相邻(上下左右没有相邻边),求取出的数的和最大为多少。
也是轮廓线方法进行处理即可,这里放出代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 20;
long long f[2][(1<<maxn)+5];
long long a[maxn+1][maxn+1];
int p[maxn+1];
int main()
{
int n, d, r;
for(register int i = 0; i <= maxn; i += 1)
p[i] = 1<<i;
long long ans;
while(~scanf("%d", &n))
{
ans = 0;
for(register int i = 0; i < n; i += 1)
for(register int j = 0; j < n; j += 1)
scanf("%lld", &a[i][j]);
d = 0;
memset(f, 0, sizeof(f));
r = p[n];
for(register int i = 0; i < n; i += 1)
for(register int j = 0; j < n; j += 1)
{
d ^= 1;
memset(f[d], 0, sizeof(f[d]));
for(register int k = 0; k < r; k += 1)
{
if(!i && k&p[j])
continue;
if(k&p[j])
{
f[d][k^p[j]] = max(f[d][k^p[j]], f[d^1][k]);
continue;
}
if(j && k&p[j-1])
{
f[d][k] = max(f[d][k], f[d^1][k]);
continue;
}
f[d][k|p[j]] = max(f[d][k|p[j]], f[d^1][k]+a[i][j]);
f[d][k] = max(f[d][k], f[d^1][k]); //不要忘了可以不选的情况
}
}
for(register int i = 0; i < r; i += 1)
ans = max(ans, f[d][i]);
cout << ans << endl;
}
return 0;
}
K 皇帝问题
〖SCOI2005 - 互不侵犯〗在 \(N\times N\) 的棋盘放上 \(K\) 个国王,使得他们互不攻击,有多少种摆放方法?注:国王可以攻击自己周围八个格子。
问题思考
由于轮廓线的特性,我们发现在八个格子的角落无法进行有效判断,所以我们需要改变一下转移的思路。这种思路其实比较暴力,但又不是完全暴力。即相邻两行状态进行枚举,同时记录已经摆放的国王个数,符合情况的状态进行转移即可。
我们可以很容易写出转移方程:\(f[i][S_i][j+\beta(S_i)]=\sum f[i-1][S_{i-1}][j],\; S_i\in G\)。
其中 \(i\) 表示第 \(i\) 行,\(S_i\) 表示当前行的状态,\(j\) 表示已经摆放的国王数,\(\beta\) 表示状态内所含国王个数,\(G\) 表示可行状态集合。
我们先看看这个 \(G\),发现连同一行的状态都有很多不合要求的,可以通过预处理进行剔除。然后在对相邻行进行可行状态转移时,我们需要将某一行的状态进行偏移,判断是否在角上有攻击情况(当然也不能忘了同一列不能有)。除此之外即可转移。
估计复杂度时:对于同一行的状态,会有多少呢?很显然是一个排列组合问题,剔除相邻(打包)情况即可。若 \(N\) 不超过 \(9\),那么一行状态最多为:
于是我们可以节省一些空间,写出如下代码:
代码一览
#include <bits/stdc++.h>
using namespace std;
long long f[10][90][82];
int n, k, cnt;
int num[90], p[10], S[90];
int bitnum(int x)
{
int y = 0;
while(x)
{
if(x & 1)
y += 1;
x >>= 1;
}
return y;
}
int main()
{
cin >> n >> k;
for(register int i = 0; i <= 9; i += 1)
p[i] = 1<<i;
int r = p[n];
for(register int i = 0; i < r; i += 1)
if(!((i<<1|i>>1)&i))
{
S[++cnt] = i;
num[cnt] = bitnum(i);
f[1][cnt][num[cnt]] = 1;
}
for(register int i = 2; i <= n; i += 1) //枚举行
for(register int s = 1; s <= cnt; s += 1) //枚举上一行状态
for(register int j = 0; j <= k; j += 1) //枚举棋子数
if(j >= num[s]) //棋子数至少要有上一行的棋子那么多
for(register int t = 1; t <= cnt; t += 1) //枚举该行状态
if(!((S[s]>>1|S[s]<<1|S[s])&S[t]))
f[i][t][j+num[t]] += f[i-1][s][j];
long long ans = 0;
for(register int i = 1; i <= cnt; i += 1)
ans += f[n][i][k];
cout << ans;
return 0;
}
同型题
〖POJ1185 - 炮兵阵地〗在有平原有山地的 \(N\times M\) 地区安置炮兵,炮兵只能处在平原,攻击范围为上下左右前进两格的位置。要使得所有炮兵不会攻击到对方,这样最多可以安置多少炮兵?
和上题相似,先处理好一行可能有多少状态,然后枚举转移即可。不过这边需要考虑的是前两行,而且炮兵数量变成了转移内容。如果设 \(f[i][S_i][S_j]\) 表示第 \(i\) 行状态 \(S_i\) 与 \(i-1\) 行状态 \(S_{i-1}\) 的时候炮兵最多摆多少个。那么转移方程为:
于是代码不难写出,此处略去。
骨牌问题
对于前面提到的骨牌摆放问题,这里也可以用类似的预处理方法进行两行两行的转移,读者可以自行思考~
子集枚举
其实旅行商问题就是此类问题,这种问题通常涉及集合的交并补运算,运用二进制操作再合适不过。这里给一道可以作为模板的题。
集合分组问题
〖UVA11825 - Hackers' Crackdown〗大意:给定 \(M\) 个集合以及全集元素个数 \(N\),求出最大的分组方案,使得每一组内集合的并集为全集。
问题思考
对集合的分组其实可以看作是变成更大的集合,只不过不同元素分组方案不同。于是我们预处理各种不同的分组方案所产生的并集,在转移的时候仅针对那些并集是全集的情况进行转移即可。
代码一览
#include <bits/stdc++.h>
using namespace std;
const int maxn = 17;
int f[1<<maxn], p[maxn], cover[1<<maxn], a[maxn];
int n, m, r, v, cas;
int main()
{
for(register int i = 0; i < maxn; i += 1)
p[i] = 1<<i;
while(scanf("%d", &n) && n)
{
r = (1<<n)-1;
memset(cover, 0, sizeof(cover));
memset(f, 0, sizeof(f));
for(register int i = 0; i < n; i += 1)
{
scanf("%d", &m);
a[i] = p[i];
for(register int j = 0; j < m; j += 1)
{
scanf("%d", &v);
a[i] |= p[v]; //集合的表示法
}
}
for(register int i = 0; i <= r; i += 1)
for(register int j = 0; j < n; j += 1)
if(i&p[j])
cover[i] |= a[j]; //获得选中集合的并集
for(register int i = 0; i <= r; i += 1) //枚举当前状态
for(register int j = i; j; j = (j-1)&i) //枚举当前选的是哪些集合(满足是 i 的子集)
if(cover[j] == r) //并起来是全集
f[i] = max(f[i], f[i-j] + 1);
printf("Case %d: %d\n", ++cas, f[r]);
}
return 0;
}
同型题
〖LeetCode698 - 划分为k个相等的子集〗有 \(N\leq 16\) 个数 \(a_i\leq 10000\),是否可以划分为恰好 \(k\) 组数,使得每组数之和相等?
显然,每组数的和 \(T\) 是固定的,等于 \(\sum a_i/n\)。因此,我们可以类似于上一题的做法,预处理不同状态产生的和是多少,转移的时候判断一下当前枚举的子集的和等于 \(T\) 即可。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 17;
int f[1<<maxn], p[maxn], cover[1<<maxn], a[maxn];
int n, k, r, alsum, v;
int main()
{
for(register int i = 0; i < maxn; i += 1)
p[i] = 1<<i;
scanf("%d%d", &n, &k);
r = (1<<n)-1;
memset(cover, 0, sizeof(cover));
memset(f, 0, sizeof(f));
for(register int i = 0; i < n; i += 1)
{
scanf("%d", &a[i]);
alsum += a[i];
}
if(alsum % k)
{
cout << "False" << endl; //不整除肯定无法分组
return 0;
}
v = alsum / k; //分成 k 组,每组和相等则必须如此
for(register int i = 0; i <= r; i += 1)
for(register int j = 0; j < n; j += 1)
if(i&p[j])
cover[i] += a[j]; //获得选中元素的和
for(register int i = 0; i <= r; i += 1) //枚举当前状态
for(register int j = i; j; j = (j-1)&i) //枚举当前选的是哪些集合(满足是 i 的子集)
if(cover[j] == v) //求和等于 v
f[i] = max(f[i], f[i-j] + 1);
cout << (f[r] == k ? "True" : "False") << endl;
return 0;
}
〖LeetCode1681 - 最小不兼容性〗有 \(N\leq 16\) 个数 \(a_i\leq N\),划分为恰好 \(k\) 个集合,使得各集合元素数量相同。定义集合的不兼容性等于最大元素与最小元素的差,求所有集合不兼容性之和的最小值。不存在这样的划分则输出 \(-1\)。
注意这里要划分成集合,即相同元素不能处于同一集合,所以我们预处理的时候要剔除这样的不合法情况。另外,题目要求各集合元素数量相同,那么在预处理的时候也要处理好这些情况。
当然,对于我的代码来说,\(a_i\) 不仅限于 \(N\) 以内的数,因为我使用了 set 进行判重。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 17;
int f[1<<maxn], p[maxn], cover[1<<maxn], val[1<<maxn], outer[1<<maxn], a[maxn];
int n, k, r, cnt, tot, v;
int nw; //暂存不兼容性
set<int> s;
set<int>::iterator it;
set<int>::reverse_iterator rit;
int bitnum(int x)
{
int ret = 0;
while(x)
{
if(x&1)
ret += 1;
x >>= 1;
}
return ret;
}
bool check(int x)
{
int ret = 0, i = 0;
s.clear();
while(x)
{
if(x&1)
{
ret += 1;
if(!s.empty() && s.find(a[i]) != s.end())
return false; //有重叠元素,不可行
s.insert(a[i]);
}
x >>= 1;
i += 1;
}
if(ret != v)
return false;
rit = s.rbegin();
int maxnum = *rit;
it = s.begin();
int minnum = *it;
nw = maxnum - minnum;
return true;
}
int main()
{
for(register int i = 0; i < maxn; i += 1)
p[i] = 1<<i;
scanf("%d%d", &n, &k);
r = (1<<n)-1;
for(register int i = 0; i <= r; i += 1)
f[i] = 0x3f3f3f3f;
cnt = tot = 0;
for(register int i = 0; i < n; i += 1)
scanf("%d", &a[i]);
v = n/k; //每组元素个数
for(register int i = 0; i <= r; i += 1) //可行方案
if(!(bitnum(i)%v)) //外层循环方案
{
outer[++tot] = i;
if(check(i))
{
cover[++cnt] = i;
val[cnt] = nw;
}
}
f[0] = 0; //初始状态
for(register int i = 1; i <= tot; i += 1) //枚举当前状态
for(register int j = 1; j <= cnt; j += 1) //枚举当前选的是哪些集合
if((cover[j]&outer[i])==cover[j])
f[outer[i]] = min(f[outer[i]], f[outer[i]-cover[j]] + val[j]);
if(f[r] > 100000)
cout << -1 << endl;
else
cout << f[r] << endl;
return 0;
}
综合问题
通常来说,题目不会出这些一眼就看出来的算法,往往会加上一些拐弯,综合其它方面设置障碍。因此我们这里需要多给一些综合性的问题,来强化实际操作中的模型构建。
并集方案问题
〖SPOJ13106 - KOSARE〗大意:设全集元素为正整数 \(1\) 到 \(M\leq 20\),给定 \(N\leq 10^6\) 个子集,选某些集合并起来得到全集,求选择方案有多少(对 \(10^9+7\) 取模)?
问题思考
我们可以设一个 \(f[S]\) 表示状态为 \(S\) 的子集(含 \(S\))的集合有多少,很显然有这样的方程:
那么,并集为 \(S\) 的子集的方案数就是 \(2^{f[S]}\)。
最后,我们对状态进行容斥。最终方案数就等于:并集为全集的子集的方案数减去并集为全集少一个元素的子集的方案数加上……
代码一览
#include <cstdio>
#define maxn (1<<20)
#define p 1000000007
int f[maxn], t[maxn], er[maxn] = {1}, s;
int ans;
int main()
{
int n, m, k, res, r;
scanf("%d%d", &n, &m);
s = (1<<m)-1;
for(register int i = 0; i < n; i += 1)
{
scanf("%d", &k);
res = 0;
for(register int j = 0; j < k; j += 1)
{
scanf("%d", &r);
res |= 1<<r-1;
}
f[res] += 1; //自己本身加上去
}
for(register int i = 0; i < m; i += 1)
for(register int j = 1; j <= s; j += 1)
if(1<<i&j)
f[j] += f[j^1<<i]; //转移部分
for(register int i = 1; i <= n; i += 1)
{
er[i] = er[i-1] << 1; //求 2 的幂
if(er[i] >= p)
er[i] -= p;
}
for(register int i = 0; i <= s; i += 1)
{
t[i] = t[i>>1] + i&1; //动态规划法统计 1 的个数
if(!(m-t[i] & 1)) //容斥符号判断
ans += er[f[i]] - 1;
else
ans -= er[f[i]] - 1;
if(ans >= p)
ans -= p;
else if(ans < 0)
ans += p;
}
printf("%d\n", ans);
return 0;
}
冲突集合问题
〖NOI2015 - 寿司晚宴〗给定 \(2\) 到 \(N\leq 500\) 的整数,\(A\) 和 \(B\) 两个人从中间取数,不能重复,可以不选,选好之后要保证 \(A\) 选的数均与 \(B\) 选的数互质。求不同选择的方案数。
问题思考
考虑 N < 20 的情况
我们可以把一个数看做是质数集合的并集,同时设 \(f[S_1][S_2]\) 表示 \(A\) 包含质数集合 \(S_1\),而 \(B\) 包含质数集合 \(S_2\) 时候的状态。转移的时候我们要保证 $S_1\cap S_2=\varnothing $,则有方程:
总方案对所有状态求和即可。
完整解答
其实我们发现:\(\sqrt{500} = 22\),每一个数拥有大于 \(19\) 的质数最多只能有一个,所以我们将它们归类,分段动态规划即可。
首先我们要预处理这些数中除了 \(20\) 以内的质数外还有哪个质数。对于没有大于 \(19\) 的质数的,按照上面方法进行动态规划即可。如果有大于 \(19\) 的质数,我们则对拥有这个相同质数的进行动态规划。
注意到拥有这个相同质数,那么只能全由一个人进行选择,另外一个人不能去选了。所以我们分 \(f_1\) 表示 \(A\) 进行选择,\(f_2\) 表示 \(B\) 进行选择,有方程:
那么在过渡阶段如何转移呢?比如从含有 \(23\) 的阶段转移到含有 \(29\) 的阶段。我们发现 \(f_1\) 和 \(f_2\) 是独立的,我们也知道 \(f\) 是当前的总情况,那么在刚过渡到新阶段的时候 \(f_1=f\),\(f_2=f\) 即可,在这个阶段结束的时候 \(f=f_1+f_2-f\) 即可(\(f_1,f_2\) 包含了两次从上一阶段转移的 \(f\))。
代码一览
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_PRIME = 8, MAXN = 500, MAX_SET = 1<<8;
const int SMALL_PRIME[] = {2,3,5,7,11,13,17,19};
pair<int, int> Split_big_small[MAXN+5];
int n, Bit[MAX_PRIME+1];
ll TotalTrans[MAX_SET][MAX_SET], p;
ll TransA[MAX_SET][MAX_SET], TransB[MAX_SET][MAX_SET];
int main()
{
cin >> n >> p;
for(register int i = 0; i <= MAX_PRIME; i += 1)
Bit[i] = 1<<i;
for(register int i = 2; i <= n; i += 1)
{
Split_big_small[i].first = i;
Split_big_small[i].second = 0;
for(register int j = 0; j < MAX_PRIME; j += 1)
{
if(Split_big_small[i].first % SMALL_PRIME[j] == 0)
Split_big_small[i].second |= Bit[j];
while(Split_big_small[i].first % SMALL_PRIME[j] == 0) //除去所有小质数
Split_big_small[i].first /= SMALL_PRIME[j];
}
}
sort(Split_big_small+2, Split_big_small+n+1); //用排序进行阶段分类
TotalTrans[0][0] = 1;
int NoBig = 2;
for(register int i = 2; i <= n && Split_big_small[i].first == 1; i += 1)
NoBig = i;
int temp, cup;
for(register int i = 2; i <= NoBig; i += 1) //单独处理小质数
{
cup = Split_big_small[i].second;
for(register int j = MAX_SET-1; ~j; j -= 1) //滚动数组,逆向枚举
{
temp = MAX_SET-1^j;
for(register int k = temp; k; k = k-1&temp)
{
if(!(cup&k))
TotalTrans[j|cup][k] = (TotalTrans[j|cup][k] + TotalTrans[j][k]) % p;
if(!(cup&j))
TotalTrans[j][k|cup] = (TotalTrans[j][k|cup] + TotalTrans[j][k]) % p;
}
TotalTrans[j|cup][0] = (TotalTrans[j|cup][0] + TotalTrans[j][0]) % p;
if(!(cup&j))
TotalTrans[j][cup] = (TotalTrans[j][cup] + TotalTrans[j][0]) % p;
}
}
for(register int j = MAX_SET-1; ~j; j -= 1) //注意分配转移
{
temp = MAX_SET-1^j;
for(register int k = temp; k; k = k-1&temp)
{
TransA[j][k] = TransB[j][k] = TotalTrans[j][k];
}
TransA[j][0] = TransB[j][0] = TotalTrans[j][0];
}
for(register int i = NoBig+1; i <= n; i += 1) //大质数分段
{
cup = Split_big_small[i].second;
if(Split_big_small[i].first != Split_big_small[i-1].first)
for(register int j = MAX_SET-1; ~j; j -= 1)
{
temp = MAX_SET-1^j;
for(register int k = temp; k; k = k-1&temp)
{
TotalTrans[j][k] = (p-TotalTrans[j][k]+(TransA[j][k]+TransB[j][k])%p)%p;
//过渡阶段进行合并
TransA[j][k] = TransB[j][k] = TotalTrans[j][k];
//分配转移
}
TotalTrans[j][0] = (p-TotalTrans[j][0]+(TransA[j][0]+TransB[j][0])%p)%p;
TransA[j][0] = TransB[j][0] = TotalTrans[j][0];
}
for(register int j = MAX_SET-1; ~j; j -= 1) //单独一人取
{
temp = MAX_SET-1^j;
for(register int k = temp; k; k = k-1&temp)
{
if(!(cup&k))
TransA[j|cup][k] = (TransA[j|cup][k] + TransA[j][k]) % p;
if(!(cup&j))
TransB[j][k|cup] = (TransB[j][k|cup] + TransB[j][k]) % p;
}
TransA[j|cup][0] = (TransA[j|cup][0] + TransA[j][0]) % p;
if(!(cup&j))
TransB[j][cup] = (TransB[j][cup] + TransB[j][0]) % p;
}
}
ll ans = 0;
for(register int j = MAX_SET-1; ~j; j -= 1) //统计答案
{
temp = MAX_SET-1^j;
for(register int k = temp; k; k = k-1&temp)
ans = (ans + (p-TotalTrans[j][k]+(TransA[j][k]+TransB[j][k])%p)%p) % p;
ans = (ans + (p-TotalTrans[j][0]+(TransA[j][0]+TransB[j][0])%p)%p) % p;
}
cout << ans << endl;
return 0;
}


