分治习题--九章算法培训课第三章笔记
1.Maximum Depth of Binary Tree
这是道简单的分治习题了
分:
左子树最大深度
右子树最大深度
治:
最大深度等于max(左子树,右子树)+1
public class Solution { public int maxDepth(TreeNode root) { if (root == null) { return 0; } int left = maxDepth(root.left); int right = maxDepth(root.right); return Math.max(left, right) + 1; } }
2.Validate Binary Search Tree
Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
该问题运用分治发的分析思路如下:
分:
判断左子树
判断右子树
治:
仅当左子树是并且右子树是而且 左子树的最大值<root.val<右子树的最小值
递归结束条件就是判断root是否为空了。不用判断叶子节点,因为判断叶子节点也是得先判断根节点然后在判断左节点和右节点是否为空
public class Solution { public boolean isValidBST(TreeNode root) { if(root == null){ return true; } if(root.left==null&&root.right==null){ return true; }else if(root.left==null){ if(isValidBST(root.right)&&root.val<getMin(root.right)) return true; // else return false; }else if(root.right==null){ if(isValidBST(root.left)&&getMax(root.left)<root.val) return true; // else return false; }else{ if(isValidBST(root.left)&&isValidBST(root.right)&& getMax(root.left)<root.val&&root.val<getMin(root.right)) return true; // else return false; } return false; } //root cannot be null public int getMin(TreeNode root){ if(root.left==null) return root.val; return getMin(root.left); } //root cannot be null public int getMax(TreeNode root){ if(root.right==null) return root.val; return getMax(root.right); } }
我的做法在判断为空的问题上太麻烦了,使用了太多的if判断,可以反其道而行之,就好很多。如下,九章的答案 .九章上面还有好几种奇妙的答案可以参考。
/* SOLUTION 3: Use the recursive version2. */ public boolean isValidBST3(TreeNode root) { // Just use the inOrder traversal to solve the problem. if (root == null) { return true; } return dfs(root, Long.MIN_VALUE, Long.MAX_VALUE); } public class ReturnType { int min; int max; boolean isBST; public ReturnType (int min, int max, boolean isBST) { this.min = min; this.max = max; this.isBST = isBST; } } // BST: // 1. Left tree is BST; // 2. Right tree is BST; // 3. root value is bigger than the max value of left tree and // smaller than the min value of the right tree. public ReturnType dfs(TreeNode root) { ReturnType ret = new ReturnType(Integer.MAX_VALUE, Integer.MIN_VALUE, true); if (root == null) { return ret; } ReturnType left = dfs(root.left); ReturnType right = dfs(root.right); // determine the left tree and the right tree; if (!left.isBST || !right.isBST) { ret.isBST = false; return ret; } // 判断Root.left != null是有必要的,如果root.val是MAX 或是MIN value,判断会失误 if (root.left != null && root.val <= left.max) { ret.isBST = false; return ret; } if (root.right != null && root.val >= right.min) { ret.isBST = false; return ret; } return new ReturnType(Math.min(root.val, left.min), Math.max(root.val, right.max), true); }
3
3. Binary Tree Preorder Traversal
很典型的分治做法:
//Version 2: Divide & Conquer public class Solution { public ArrayList<Integer> preorderTraversal(TreeNode root) { ArrayList<Integer> result = new ArrayList<Integer>(); // null or leaf if (root == null) { return result; } // Divide ArrayList<Integer> left = preorderTraversal(root.left); ArrayList<Integer> right = preorderTraversal(root.right); // Conquer result.add(root.val); result.addAll(left); result.addAll(right); return result; } }
当然前序遍历问题还有比较常用的几种解法如下:
使用堆栈的非递归形式:
public class Solution { public List<Integer> preorderTraversal(TreeNode root) { Stack<TreeNode> stack = new Stack<TreeNode>(); List<Integer> preorder = new ArrayList<Integer>(); if (root == null) { return preorder; } stack.push(root); while (!stack.empty()) { TreeNode node = stack.pop(); preorder.add(node.val); if (node.right != null) { stack.push(node.right); } if (node.left != null) { stack.push(node.left); } } return preorder; } } //Version 1: Traverse public class Solution { public ArrayList<Integer> preorderTraversal(TreeNode root) { ArrayList<Integer> result = new ArrayList<Integer>(); traverse(root, result); return result; } private void traverse(TreeNode root, ArrayList<Integer> result) { if (root == null) { return; } result.add(root.val); traverse(root.left, result); traverse(root.right, result); } }
和仿后序方法:
public class Solution { public List<Integer> preorderTraversal(TreeNode root) { ArrayList<Integer> result = new ArrayList<Integer>(); if(root == null) return result; Stack<TreeNode> stack = new Stack<TreeNode>(); stack.push(root); TreeNode prev = null; while(!stack.empty()){ TreeNode curr = stack.peek(); if(prev==null||curr==prev.left||curr==prev.right){ result.add(curr.val); if(curr.left!= null){ stack.push(curr.left); }else if(curr.right!=null){ stack.push(curr.right); } else{ stack.pop(); } }else if(prev==curr.left){ if(curr.right!=null){ stack.push(curr.right); } else{ stack.pop(); } }else if(prev==curr.right){ stack.pop(); } prev = curr; } return result; } }
这里是些前序遍历的模板

Template 1: Traverse public class Solution { public void traverse(TreeNode root) { if (root == null) { return; } // do something with root traverse(root.left); // do something with root traverse(root.right); // do something with root } } Tempate 2: Divide & Conquer public class Solution { public ResultType traversal(TreeNode root) { // null or leaf if (root == null) { // do something and return; } // Divide ResultType left = traversal(root.left); ResultType right = traversal(root.right); // Conquer ResultType result = Merge from left and right. return result; } }
4.Binary Tree Maximum Path Sum
Given a binary tree, find the maximum path sum.
The path may start and end at any node in the tree.
For example:
Given the below binary tree,
1
/ \
2 3
Return 6.
首先九章的答案思路跟课堂上讲的是一样的,不过我觉得有句话表述的不是非常准确。

我觉得这里的1.的条件下的话是有问题的,不可全信。
首先,这里如果使用分治递归的算法的话函数应该返回两个数值即max,当前子树最大路径长度及maxSingle,当前子树通过根节点的最大子路径长度(以供上层调用时候合成通过根节点的最大路径长度时使用)。因此定义了一个ResultType的inner class。
而最大路径长度有两种可能,即来自左、右子树的最大路径长度的最大者;或者是贯穿左右子树的路径中的最大者。
左右子树的最大路径长度非常好求可以通过递归获取。而贯穿左右子树的最大者就是在分治算法中治的部分实现的关键部分。它是穿过根节点的,所以根节点可以不管其正负。但是不能使左子树的maxSingle+右子树maxSingle+root.val。因为左右子树的maxSingle有可能是负的,那我们就没必要加进来了。因此要如下实现:
int cross = root.val; //定义穿过根节点的路径
cross += Math.max(left.maxSingle,0);
cross += Math.max(right.maxSingle,0);
在处理完治的部分后,要构建穿过当前节点的maxSingle的值,这里需要注意的就是 如果其左右子树的maxSingle有负的,我们就可以直接返回root.value。即如下所示:
ret.maxSingle = Math.max(Math.max(left.maxSingle,right.maxSingle),0)+root.val;
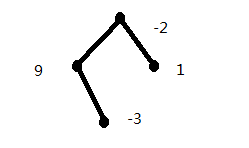
就如9节点时候,maxSingle就应该取其自身。
整体程序还是按照九章的答案来的,只不过是理解了之后默写处理的。
public class Solution { //因为这里需要记录一个是总体最大路径,和一个单路最大路径因此需要构造一个ResultType public class ResultType{ int max; int maxSingle; ResultType(int max, int maxSingle){ this.max = max; this.maxSingle = maxSingle; } } public ResultType helper(TreeNode root){ ResultType ret = new ResultType(Integer.MIN_VALUE,Integer.MIN_VALUE); if(root == null){ return ret; } //divide ResultType left = helper(root.left); //左子树最大路径 ResultType right = helper(root.right); //右子树最大路径 //conquer int cross = root.val; //定义穿过根节点的路径 cross += Math.max(left.maxSingle,0); cross += Math.max(right.maxSingle,0); ret.max = Math.max(Math.max(left.max,right.max),cross); ret.maxSingle = Math.max(Math.max(left.maxSingle,right.maxSingle),0)+root.val; return ret; } public int maxPathSum(TreeNode root) { return helper(root).max; } }
5.Binary Search Tree Iterator
Implement an iterator over a binary search tree (BST). Your iterator will be initialized with the root node of a BST.
Calling next() will return the next smallest number in the BST.
Note: next() and hasNext() should run in average O(1) time and uses O(h) memory, where h is the height of the tree.
Credits:
Special thanks to @ts for adding this problem and creating all test cases.
/** * Definition for binary tree * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ public class BSTIterator { TreeNode root; Stack<TreeNode> stack = new Stack<TreeNode>(); TreeNode p; public BSTIterator(TreeNode root) { this.root = root; p=root; } /** @return whether we have a next smallest number */ public boolean hasNext() { return !stack.isEmpty()||p!=null; } /** @return the next smallest number */ public int next() { while(this.hasNext()){ if(p!=null){ stack.push(p); p=p.left; }else{ p=stack.pop(); int tmp = p.val; p=p.right; return tmp; } } return -1; } } /** * Your BSTIterator will be called like this: * BSTIterator i = new BSTIterator(root); * while (i.hasNext()) v[f()] = i.next(); */
6.Search Range in Binary Search Tree
Given two values k1 and k2 (where k1 < k2) and a root pointer to a Binary Search Tree. Find all the keys of tree in range k1 to k2. i.e. print all x such that k1<=x<=k2 and x is a key of given BST. Return all the keys in ascending order.
For example, if k1 = 10 and k2 = 22, then your function should print 12, 20 and 22.
20
/ \
8 22
/ \
4 12
此题也是很经典的分治算法。先假设左右子树做好了,只用判断根处的处理结果就可以了。
public ArrayList<Integer> searchRange(TreeNode root, int k1, int k2) { // write your code here ArrayList<Integer> ret = new ArrayList<Integer>(); if(root==null) return ret; ArrayList<Integer> llist = searchRange(root.left,k1,k2); ArrayList<Integer> rlist = searchRange(root.right,k1,k2); if(root.val>k2){ ret.addAll(llist); }else if(root.val<k1){ ret.addAll(rlist); }else{ ret.addAll(llist); ret.add(root.val); ret.addAll(rlist); } return ret; }
23333333333333333333333333分界线333333333333333333333333333333
以下是课堂笔记:
归并排序和快速排序是典型的分治算法。但是稍有不同的是快速排序是先整体有序,后局部有序;而归并排序则是先局部有序,再整体有序。
而且归并排序虽然比较浪费存储空间,需要数组来回复制,但是其是稳定排序;而快速排序则是不稳定的。这部分内容稍后我也会google后更新。
关于时间复杂度的分析,有个树形分析法,待有时间更新,课堂时间太紧没记全。
概率题,待查待更新。
关于Java中Queue的虚类问题,待更新。
还有一些典型的课件上的习题,我也会更新后整理在这里的,这里是我刷题做笔记的地方,当然九章算法上有更详细的答案,我只是会加一些自己的理解,不嫌弃的话可以瞧瞧,嘿嘿,谢谢大家了。






【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步