Java数据结构四之——二叉树的前、中、后序遍历

程序来自Program Creek

前序遍历：

Preorder binary tree traversal is a classic interview problem about trees. The key to solve this problem is to understand the following:

1. What is preorder? (parent node is processed before its children)
2. Use Stack from Java Core library

It is not obvious what preorder for some strange cases. However, if you draw a stack and manually execute the program, how each element is pushed and popped is obvious.

The key to solve this problem is using a stack to store left and right children, and push right child first so that it is processed after the left child.

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}
 
public class Solution {
    public ArrayList<Integer> preorderTraversal(TreeNode root) {
        ArrayList<Integer> returnList = new ArrayList<Integer>();
 
        if(root == null)
            return returnList;
 
        Stack<TreeNode> stack = new Stack<TreeNode>();
        stack.push(root);
 
        while(!stack.empty()){
            TreeNode n = stack.pop();
            returnList.add(n.val);
 
            if(n.right != null){
                stack.push(n.right);
            }
            if(n.left != null){
                stack.push(n.left);
            }
 
        }
        return returnList;
    }
}

 　　以上程序的思想类似于深度优先搜索（DFS）了，只不过在这里是先遍历当前节点，然后左边优先遍历了！

　　由于我是先看的后序遍历，因此，自己实现的前序遍历便按照后序遍历的样子写的。程序如下：

public class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        ArrayList<Integer> result = new ArrayList<Integer>();
 
        if(root == null)
            return result; 
 
        Stack<TreeNode> stack = new Stack<TreeNode>();
        stack.push(root);
 
        TreeNode prev = null;
        while(!stack.empty()){
            TreeNode curr = stack.peek();
            
            if(prev==null||curr==prev.left||curr==prev.right){
                
                 result.add(curr.val);
                 
                 if(curr.left!= null){
                    stack.push(curr.left);
                }else if(curr.right!=null){
                    stack.push(curr.right);
                }
                else{
                    stack.pop();
                }
            }else if(prev==curr.left){
                if(curr.right!=null){
                    stack.push(curr.right);
                }
                else{
                    stack.pop();
                }
            }else if(prev==curr.right){
                stack.pop();
            }
            
            prev = curr;
        }
        return result;
    }
}

 九章算法中的各种版本答案

Version 0: Non-Recursion (Recommend)
/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<TreeNode>();
        List<Integer> preorder = new ArrayList<Integer>();
        
        if (root == null) {
            return preorder;
        }
        
        stack.push(root);
        while (!stack.empty()) {
            TreeNode node = stack.pop();
            preorder.add(node.val);
            if (node.right != null) {
                stack.push(node.right);
            }
            if (node.left != null) {
                stack.push(node.left);
            }
        }
        
        return preorder;
    }
}

//Version 1: Traverse
public class Solution {
    public ArrayList<Integer> preorderTraversal(TreeNode root) {
        ArrayList<Integer> result = new ArrayList<Integer>();
        traverse(root, result);
        return result;
    }

    private void traverse(TreeNode root, ArrayList<Integer> result) {
        if (root == null) {
            return;
        }

        result.add(root.val);
        traverse(root.left, result);
        traverse(root.right, result);
    }
}

//Version 2: Divide & Conquer
public class Solution {
    public ArrayList<Integer> preorderTraversal(TreeNode root) {
        ArrayList<Integer> result = new ArrayList<Integer>();
        // null or leaf
        if (root == null) {
            return result;
        }

        // Divide
        ArrayList<Integer> left = preorderTraversal(root.left);
        ArrayList<Integer> right = preorderTraversal(root.right);

        // Conquer
        result.add(root.val);
        result.addAll(left);
        result.addAll(right);
        return result;
    }
}

 

中序遍历：

The key to solve inorder traversal of binary tree includes the following:

1. The order of "inorder" is: left child -> parent -> right child
2. Use a stack to track nodes
3. Understand when to push node into the stack and when to pop node out of the stack

//Definition for binary tree
public class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode(int x) { val = x; }
 }
 
public class Solution {
    public ArrayList<Integer> inorderTraversal(TreeNode root) {
        // IMPORTANT: Please reset any member data you declared, as
        // the same Solution instance will be reused for each test case.
         ArrayList<Integer> lst = new ArrayList<Integer>();
 
        if(root == null)
            return lst; 
 
        Stack<TreeNode> stack = new Stack<TreeNode>();
        //define a pointer to track nodes
        TreeNode p = root;
 
        while(!stack.empty() || p != null){
 
            // if it is not null, push to stack
            //and go down the tree to left
            if(p != null){
                stack.push(p);
                p = p.left;
 
            // if no left child
            // pop stack, process the node
            // then let p point to the right
            }else{
                TreeNode t = stack.pop();
                lst.add(t.val);
                p = t.right;
            }
        }
 
        return lst;
    }
}

 　　依旧根究后续遍历的总体思路来进行遍历的话，分区什么时候向下走，什么时候遍历，左上，右上的情况，就非常好遍历了。这种思想还是比较好，比较通用的。程序如下：

public class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
         ArrayList<Integer> result = new ArrayList<Integer>();
 
        if(root == null)
            return result; 
 
        Stack<TreeNode> stack = new Stack<TreeNode>();
        stack.push(root);
 
        TreeNode prev = null;
        while(!stack.empty()){
            TreeNode curr = stack.peek();
            if(prev==null||curr==prev.left||curr==prev.right){
                if(curr.left!=null){
                    stack.push(curr.left);
                }else if(curr.right!=null){
                    result.add(curr.val);
                    stack.push(curr.right);
                }else{
                     result.add(curr.val);
                     stack.pop();
                }
            }else if(prev==curr.left){
                result.add(curr.val);
                if(curr.right!=null){
                    stack.push(curr.right);
                }else{
                    stack.pop();
                }
                
            }else if(prev==curr.right){
                stack.pop();
            }
            prev=curr;
        }//while
        return result;
    }
}

 

 

后序遍历：

递归算法：

　　递归算法很简单。程序来自九章算法。

 

//Recursive
public ArrayList<Integer> postorderTraversal(TreeNode root) {
    ArrayList<Integer> result = new ArrayList<Integer>();

    if (root == null) {
        return result;
    }


    result.addAll(postorderTraversal(root.left));
    result.addAll(postorderTraversal(root.right));
    result.add(root.val);

    return result;   
}

 

 

 

 

迭代解法：

 　　使用两个指针prev和curr分别指向当前和上次访问的节点。

总体原则遵循：

　　1.先经过左子树，遍历之，

　　2.经过父节点（此时是从左上来的），获得右节点，

　　3.经过右子树，遍历之，

　　4.再次经过父节点（此时是从右上来的），

　　5.遍历父节点。

首先明确以下事实：

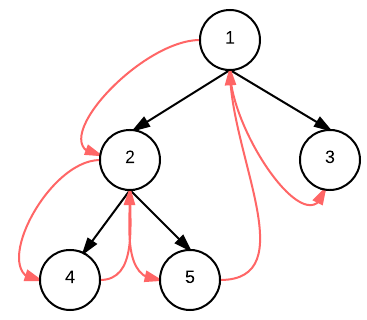
　　①当向左一直延伸时，curr始终在prev的前方（下面），也即满足如下条件：curr==prev.left。②当向右走的时候，满足：curr == prev.right。

　　③当从左端上来的时候满足：prev == curr.left；④相应的当从右端上来的时候满足：prev == curr.right。　

遍历步骤：

　　首先，我们向下走，沿着路径向左延伸直至左叶子或者没有左子节点的节点为止，对应①。当子树遍历完，才会向上走，当左节点遍历完或者左子树遍历完会从左向上走，此时对应③；此时“第一次经过父节点”，如果右子树不为空，获取右子树（将右子节点压栈），然后向下走，对应②，经过右子树（当便遍历右子树时，仍然先从左子子树下手，此时便循环上述①过程）。当右子树遍历完成之后，从右而上，对应④。此时是“第二次经过父节点”，遍历父节点。继续向上走，继续判断是从左而上③，还是从右而上④。

　　有了以上思路，程序就好写了。我们只需知道判断条件：何时需要向下走，何时需要遍历节点，即可书写while循环遍历二叉树了。

判断条件：

　　这也很明确了，A)当初始时刻prev==null时；当遍历完左节点，第一次经过父节点时，curr == prev.left；当遍历完左子树，第一次经过父节点，并且父节点的右子树不为空时，curr == prev.right，我们需要向下走。

　　AA)当curr == prev.right，并且无左右子节点时；B)当从右而上，右子树遍历完成，第二次经过父节点时,prev==curr.right；C)当从左而上，第一次经过父节点，但父节点没有右子树时，prev == curr.left，我们需要遍历节点。

见程序，程序来自Program creek

 

The key to to iterative postorder traversal is the following:

1. The order of "Postorder" is: left child -> right child -> parent node.
2. Find the relation between the previously visited node and the current node
3. Use a stack to track nodes

As we go down the tree, check the previously visited node. If it is the parent of the current node, we should add current node to stack. When there is no children for current node, pop it from stack. Then the previous node become to be under the current node for next loop.

 1 //Definition for binary tree
 2 public class TreeNode {
 3     int val;
 4     TreeNode left;
 5     TreeNode right;
 6     TreeNode(int x) { val = x; }
 7 }
 8  
 9  
10 public class Solution {
11     public ArrayList<Integer> postorderTraversal(TreeNode root) {
12  
13         ArrayList<Integer> lst = new ArrayList<Integer>();
14  
15         if(root == null)
16             return lst; 
17  
18         Stack<TreeNode> stack = new Stack<TreeNode>();
19         stack.push(root);
20  
21         TreeNode prev = null;
22         while(!stack.empty()){
23             TreeNode curr = stack.peek();
24  
25             // go down the tree.
26             //check if current node is leaf, if so, process it and pop stack,
27             //otherwise, keep going down
28             if(prev == null || prev.left == curr || prev.right == curr){
29                 //prev == null is the situation for the root node
30                 if(curr.left != null){
31                     stack.push(curr.left);
32                 }else if(curr.right != null){
33                     stack.push(curr.right);
34                 }else{
35                     stack.pop();
36                     lst.add(curr.val);
37                 }
38  
39             //go up the tree from left node    
40             //need to check if there is a right child
41             //if yes, push it to stack
42             //otherwise, process parent and pop stack
43             }else if(curr.left == prev){
44                 if(curr.right != null){
45                     stack.push(curr.right);
46                 }else{
47                     stack.pop();
48                     lst.add(curr.val);
49                 }
50  
51             //go up the tree from right node 
52             //after coming back from right node, process parent node and pop stack. 
53             }else if(curr.right == prev){
54                 stack.pop();
55                 lst.add(curr.val);
56             }
57  
58             prev = curr;
59         }
60  
61         return lst;
62     }
63 }

 

 

 

尚待实践和整理