Dijkstra在路由选择中的应用

Dijkstra在路由选择中的应用

前言背景

OSPF协议(Open Shortest Path First，开放最短路径优先)是在1989年由互联网工程任务组(IETF)正式发布。它能有效地解决RIP和IGRP等距离矢量协议存在的缺陷。具体优点如下：

1. 收敛速度快：OSPF采用一种可靠的扩散(flooding)机制根据网络拓扑变化来更新邻居路由器。路由发生改变时只发送产生的路由更新信息。这两点，再加上整个网络在OSPF域中所有路由器上的拓扑都几乎完全一样的特点，使得OSPF在某条链路出现问题时能够比RIP和IGRP更迅速的收敛。

2. 支持VLSM、超网以及汇总功能OSPF采用汇总功能和VLSM来节省地址空间。能够更高效地进行路由。

3. 存根区域路由：OSPF采用存根区域路由大大减小了路由表的规模。这也是OSPF支持大型网络的一个原因。

4. 基于路由代价(Cost)的可变度量OSPF采用可变路由代价度量标准来决定路由选择。

5. 支持类型1和类型2(MD5)的认证方式．OSPF能够通过类型1的明文密码或是类型2的MD5加密认证方式来确保安全可靠的路由传输。

原理描述

OSPF区中的每个路由器都具有一个完全相同的链路状态数据库。该链路状态数据库描述了路由器、它们的链路，以及链路的代价。把路由器看作图的顶点，把它们之间的链路看作图的边，把链路的代价看作图的边的权，可把链路状态数据库转换成图。当链路状态数据库转换成一张图后，就可以应用Dijkstra算法来计算出从一点出发到其他所有点的最短路径，即可以计算出路由表。具体的算法如下：把要进行路由计算的路由器加入到最短路径树中，把它所有的邻居加入到可选列表中，并把这些路由器的代价设为刚才加入到最短路径树中的路由器相连的链路代价。接着从可选列表中选出一个代价最小的路由器 加入到最短路径树中，并把它的所有邻居加入到可选列表中。只要可选列表不为空，这个过程一直进行下去。在该算法执行完成后，就可以生成路由器的最短路径树，根据最短路径树，我们就可以得出路由器的路由表。

实验截图

图1

图2

图3

代码

#include<iostream>
#define N 501	//最大路由器数量 
#define INF 100000	//路径最大代价 

using namespace std;

int n;	//初始路由器数量
int adj[N][N];	//邻接矩阵

void init();
void print();
void ospf(int);

int main()
{
	init();		//初始化链路状态 
	print();	//打印初始链路状态 
	for(int i=1;i<=n;i++)
		ospf(i);	//dijkstra算法寻找当前路由器到达各路由器最小代价并打印路由表 
	return 0;
}

//初始化链路状态
void init()
{
	cout<<"请输入路由器个数:"<<endl;
	cin>>n;
	int x,y,z;	//x,y:路由器，z:代价 
	cout<< "请输入路由器间的连接状态，如路由器1 路由器2 代价,0 0 0表示输入结束"<<endl;
	while(cin>>x>>y>>z&&!(!x&&!y&&!z))
	{
		adj[x][y]=z;
		adj[y][x]=z;
	}
	for(int i=1;i<n;i++)
	{
		for(int j=i+1;j<=n;j++)
		{
			if(!adj[i][j])	//两路由器不相邻时 
			{
				adj[i][j]=INF;
				adj[j][i]=INF;
			}
		}
	}
}

//打印初始链路状态 
void print()
{
	cout<<"初始链路状态如下，#表示两路由不相邻" <<endl; 
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(adj[i][j]==INF) cout<<"# ";
			else cout<<adj[i][j]<<' ';
		}
		cout<<endl;
	}
}

//自适应生成最小代价路由表 
void ospf(int x)
{
	int dis[N];		//代价数组，dis[i]的值表示路由x到路由i的代价 
	int next[N];	//相邻路由
	int vis[N]={0};	//对已确定到路由x最小代价值的路由进行标记
	vis[x]=1;
	for(int i=1;i<=n;i++) 	//对邻接矩阵初始值进行拷贝 
	{
		dis[i]=adj[x][i];
		next[i]=i;
	}
	int index=x;	//赋初值，后面要用来做判断
	for(int i=1;i<=n;i++)
	{
		int min_num=INF;
		for(int j=1;j<=n;j++)
		{
			if(!vis[j]&&dis[j]<min_num)	//未标记且到源点的代价比当前最小代价小 
			{
				min_num=dis[j];	//记录与路由i相邻路由中的最小代价
				index=j;	//记录相邻最小代价路由的编号
			}
		}
		if(index==x) return;	//index值没变说明没访问过的路由器中没有与i直接相邻的
		vis[index]=1;	//标记
		for(int j=1;j<=n;j++)
		{
			if(dis[j]>dis[index]+adj[index][j]&&!vis[j])	//如果通过中间路由器能实现更小代价到达路由器j则更新数组 
			{
				dis[j]=dis[index]+adj[index][j];
				next[j]=next[index];
			}
		}
	}
	cout<<"*****************"<<endl;
	cout<<"路由"<<x<<" 下一跳 "<<"代价"<<endl;
	for(int i=1;i<=n;i++)
	{
		if(x==i) continue;
		cout<<i<<"       "<<next[i]<<"     "<<dis[i]<<endl;
	}
	cout<<endl;
}

结果分析

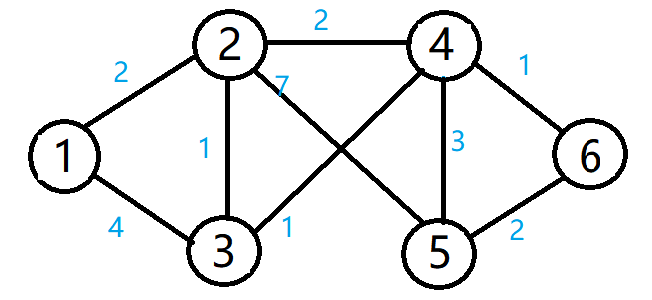
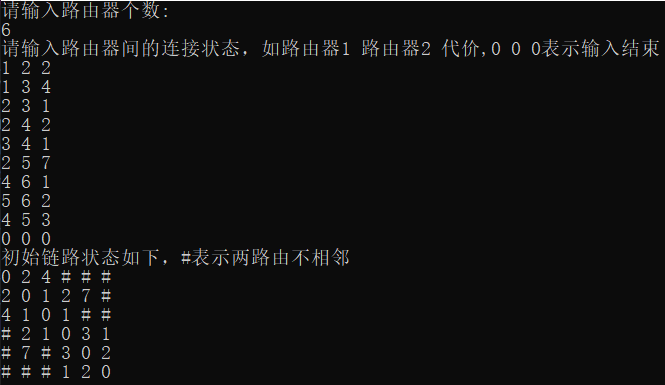
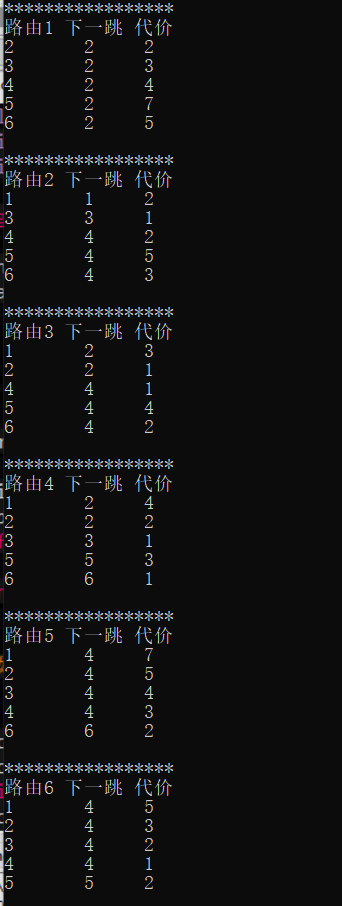
如实验截图中所示，图1是一个无向图，将6个结点看作6台路由器，边上的值看作这条路径的代价，对链路状态进行初始化并打印，如图2。每台路由器通过Dijkstra算法以自身作为源点寻找到达其他路由器的最小代价并打印各自的路由表，如图3。

以路由1到路由6为例，先查路由1的路由表，可以看到到达路由6需要的最小代价为5以及下一跳应该去路由2，再查看路由2的路由表可知要去路由6下一跳应该去路由4，再查看路由4的路由表可知下一跳可以直接到达路由6.