「HDU」5434 Peaceful Small Elephant （状压）

题意：原题在这

给出一个棋盘大小，一只小象可以跳这一格直角顶点所对的格子（及左上右上左下右下），且两只互不能攻击的小象还可以合体，合体之后攻击范围进行合并（见图）。求有多少种能使小象互不攻击的摆放方案

 

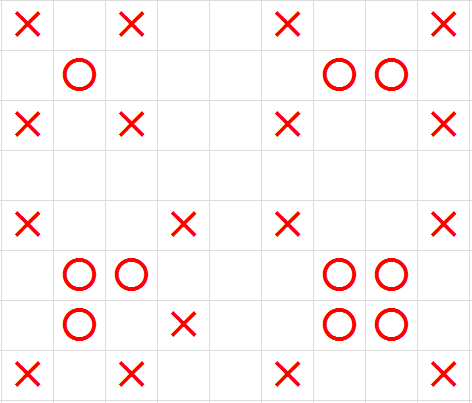
做法：

 

1. 由题可知：合并的小象其实是攻击范围变小了

2. 如果坐标（i,j）,（i+1,j+1）存在小象，那么必须保证（i+1,j)，（i，j+1)两个位置至少有一个棋子，可以得到状态转移矩阵。

3. 然后状压+矩阵快速幂

 

代码：

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define mod 1000000007
#define inf 9999999999
using namespace std;
int n,m,p,digit;
bool w[128][128];

struct node
{
    long long r[1<<8][1<<8];
}ans,base;

node multi(node a,node b)
{
    node count;
    for(int i=0;i<digit;i++)
    for(int j=0;j<digit;j++)
    {
        count.r[i][j]=0;
    }
    for(int i=0;i<digit;i++)
    for(int j=0;j<digit;j++)
    for(int k=0;k<digit;k++)
    {
        count.r[i][j]=(count.r[i][j]+(long long)(a.r[i][k]*b.r[k][j])%mod)%mod;
    }
    return count;
}

node pow(long long p)
{
    node result;
    for(int i=0;i<(1<<8);i++)
    for(int j=0;j<(1<<8);j++)
    {
        result.r[i][j]=0;
    }
    for(int i=0;i<(1<<m);i++)
    {
        result.r[i][i]=1;
    }
    for(int i=0;i<(1<<m);i++)
    for(int j=0;j<(1<<m);j++)
    {
        base.r[i][j]=w[i][j];
    }
    while(p)
    {
        if(p%2) result=multi(result,base);
        p>>=1;
        base=multi(base,base);
    }
    return result;
}

bool check(int x,int y)//是否冲突
{
    for(int i=0;i<m;i++)
    {
        int k=1<<i;
        if(x&k)
        {
            if(i!=0)
            {
                if((y&(1<<i-1))&&!(x&(1<<i-1))&&!(y&(1<<i))) return false;
            }
            if(i!=m-1)
            {
                if((y&(1<<i+1))&&!(x&(1<<i+1))&&!(y&(1<<i))) return false;
            }
        }
    }
    return true;
}

void matrix()
{
    for(int i=0;i<digit;i++)
    for(int j=0;j<digit;j++)
    {
        if(check(i,j)) w[i][j]=1;
    }
}

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        memset(w,0,sizeof(w));
        digit=1<<m;
        matrix();
        node ans1=pow(n);
        node ans2;
        for(int i=0;i<128;i++)
        for(int j=0;j<128;j++)
        {
            ans2.r[i][j]=0;
            ans2.r[0][0]=1;
        }
        ans2=multi(ans2,ans1);
        int sum=0;
        for(int i=0;i<digit;i++)
        for(int j=0;j<digit;j++)
        {
            sum=(sum+ans2.r[i][j])%mod;
        }
        cout<<sum<<endl;
    }
    return 0;
}