机房测试10.6
砖块
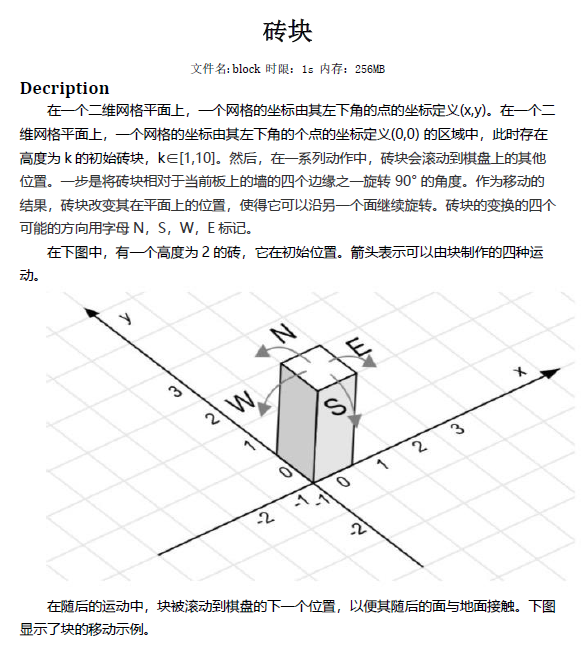


很简单的水题,写起来也很简单。
模拟写的很短,是否也是码力的体现?
#include<cstdio>
#include<cstring>
#include<map>
#define FN "block"
int mp[1105][1105],dao,ans;
char s[105];
int x,y,dx[4]={0,0,-1,1},dy[4]={1,-1,0,0};
std::map<char,int> m;
void init() {
memset(mp,0,sizeof(mp));
mp[550][550]=1;
ans=x=y=0;
dao=-1;
}
int main() {
freopen(FN".in","r",stdin);
freopen(FN".out","w",stdout);
m['N']=0,m['S']=1,m['W']=2,m['E']=3;
int T;scanf("%d",&T);
while(T--) {
init();
int k;scanf("%d",&k);
scanf("%s",s+1);
int len=strlen(s+1);
for(int i=1;i<=len;i++) {
x+=dx[m[s[i]]];
y+=dy[m[s[i]]];
if(!~dao) {
for(int j=0;j<k;j++)
if(++mp[x+dx[m[s[i]]]*j+550][y+dy[m[s[i]]]*j+550]>ans)
ans=mp[x+dx[m[s[i]]]*j+550][y+dy[m[s[i]]]*j+550];
dao=m[s[i]];
}
else if((dao^m[s[i]])==1) {
if(++mp[x+550][y+550]>ans) ans=mp[x+550][y+550];
dao=-1;
}
else if(dao==m[s[i]]) {
x+=dx[m[s[i]]]*(k-1),y+=dy[m[s[i]]]*(k-1);
if(++mp[x+550][y+550]>ans) ans=mp[x+550][y+550];
dao=-1;
}
else {
for(int j=0;j<k;j++)
if(++mp[x+dx[dao]*j+550][y+dy[dao]*j+550]>ans)
ans=mp[x+dx[dao]*j+550][y+dy[dao]*j+550];
}
}
if(!~dao) printf("%d\n%d\n",x,y);
else if(dao==0 || dao==3) {
for(int j=0;j<k;j++) printf("%d%c",x+dx[dao]*j,j==k-1?'\n':' ');
for(int j=0;j<k;j++) printf("%d%c",y+dy[dao]*j,j==k-1?'\n':' ');
}
else {
for(int j=k-1;j>=0;j--) printf("%d%c",x+dx[dao]*j,j?' ':'\n');
for(int j=k-1;j>=0;j--) printf("%d%c",y+dy[dao]*j,j?' ':'\n');
}
printf("%d\n",ans);
}
return 0;
}
可以不用map,但是我懒得改了。
翻转有好几种情况,只要去想,还是不会漏的(如果漏了过不了样例)
数字

真的堪称神仙题,题解至今没有看懂。
威尔逊定理加上balabala可以解决\(k=1\)的情况。
预处理1e7阶乘%1e7可以50分,%1e5只有20分。
std的代码(有高精度):
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int con=100000000;
const int wei=8;
class Int{
public:long long a[100];
void read(){
memset(a,0,sizeof(a));
char S[105]={0}; int len=0;
scanf("%s",S+1); len=strlen(S+1);
for (int i=1;i<=len/2;i++) swap(S[i],S[len-i+1]);
for (int i=1;i<=len;i++) S[i]-='0';
a[0]=0;
for (int i=1;i<=len;i+=8){
a[0]++;
for (int j=i+7;j>=i;j--)
a[a[0]]=a[a[0]]*10+S[j];
}
}
void getdata(int x){memset(a,0,sizeof(a));while (x){a[++a[0]]=x%con;x=x/con;}}
Int(int x=0){
getdata(x);
}
void pri(bool flag){
if (a[0]==0||(a[0]==1&&a[1]==0)){printf("0");if (flag)printf("\n");return;}
printf("%lld",a[a[0]]);
for (int i=a[0]-1;i;i--)
printf("%08lld",a[i]);
if (flag)printf("\n");
}
bool operator <(const Int &X){
if (a[0]<X.a[0])return true;if (a[0]>X.a[0])return false;
for (int i=a[0];i;i--){if (a[i]<X.a[i])return true;if (a[i]>X.a[i])return false;}
return false;
}
bool operator >(const Int &X){
if (a[0]<X.a[0])return false;if (a[0]>X.a[0])return true;
for (int i=a[0];i;i--){if (a[i]<X.a[i])return false;if (a[i]>X.a[i])return true;}
return false;
}
bool operator <=(const Int &X){
if (a[0]<X.a[0])return true;if (a[0]>X.a[0])return false;
for (int i=a[0];i;i--){if (a[i]<X.a[i])return true;if (a[i]>X.a[i])return false;}
return true;
}
bool operator >=(const Int &X){
if (a[0]<X.a[0])return false;if (a[0]>X.a[0])return true;
for (int i=a[0];i;i--){if (a[i]<X.a[i])return false;if (a[i]>X.a[i])return true;}
return true;
}
bool operator ==(const Int &X){
if (a[0]!=X.a[0])return false;for (int i=a[0];i;i--)if (a[i]!=X.a[i])return false;
return true;
}
Int operator +(const Int &X){
Int c;memset(c.a,0,sizeof(c.a));
for (int i=1;i<=a[0]||i<=X.a[0];i++)
{c.a[i]=c.a[i]+a[i]+X.a[i];c.a[i+1]+=c.a[i]/con;c.a[i]%=con;}
c.a[0]=max(a[0],X.a[0]);if (c.a[c.a[0]+1])c.a[0]++;
return c;
}
Int operator +(int num){
Int c;memcpy(c.a,a,sizeof(c.a));c.a[1]+=num;
for (int i=1;i<=c.a[0]&&c.a[i]>=con;i++)c.a[i]-=con,c.a[i+1]++;
while (c.a[c.a[0]+1])c.a[0]++;
return c;
}
Int operator -(const Int &X){
Int c;memcpy(c.a,a,sizeof(c.a));
for (int i=1;i<=a[0];i++){c.a[i]=c.a[i]-X.a[i];if (c.a[i]<0){c.a[i+1]--;c.a[i]+=con;}}
while (c.a[0]&&!c.a[c.a[0]])c.a[0]--;
return c;
}
Int operator -(int num){
Int c;memcpy(c.a,a,sizeof(c.a));c.a[1]-=num;
for (int i=1;i<=c.a[0]&&c.a[i]<0;i++)c.a[i]+=con,c.a[i+1]--;
while (c.a[0]&&!c.a[c.a[0]])c.a[0]--;
return c;
}
Int operator *(const Int &X){
Int c;memset(c.a,0,sizeof(c.a));
for (int i=1;i<=a[0];i++)for (int j=1;j<=X.a[0];j++)
{c.a[i+j-1]+=a[i]*X.a[j];c.a[i+j]+=c.a[i+j-1]/con;c.a[i+j-1]%=con;}
c.a[0]=max(a[0]+X.a[0]-1,0ll);if (c.a[a[0]+X.a[0]]>0)c.a[0]++;
return c;
}
Int operator *(int num){
Int c;memset(c.a,0,sizeof(c.a));
for (int i=1;i<=a[0];i++){c.a[i]+=a[i]*num;if (c.a[i]>=con){c.a[i+1]+=c.a[i]/con;c.a[i]%=con;}}
c.a[0]=a[0];if (c.a[c.a[0]+1]>0)c.a[0]++;
return c;
}
Int operator /(int num){
Int c;memset(c.a,0,sizeof(c.a));
long long x=0;for (int i=a[0];i;i--){x=x*con+a[i];c.a[i]=x/num;x=x%num;}
c.a[0]=a[0];if (c.a[0]&&!c.a[c.a[0]])c.a[0]--;
return c;
}
int operator %(int num){
int ret=0;
for (int i=a[0];i;i--)
ret=((ll)ret*con+a[i])%num;
return ret;
}
};
inline int Pow(int a,int b,int p){
int ret=1;
for (int i=1;i<=b;i++) ret=ret*a%p;
return ret;
}
Int N,K,K0;
int k;
int S[1005],m;
inline void Pre(){
Int t=N; K0.getdata(0);
while (!(t==0)) K0=K0+t/5,t=t/5;
}
int ans[200][200];
int a[200];
inline int Solve(){
int phi=k==1?4:(k==2?4*5:4*5*5);
int mod2=0,mod5,k2=Pow(2,k,2333),k5=Pow(5,k,2333);
for (int i=0;i<k2*k5;i++) ans[i%k2][i%k5]=i;
int inv=Pow(2,phi-1,k5),Inv=Pow(inv,K0%phi,k5);
a[0]=1;
for (int i=1;i<k5;i++){
int t=i; if (t%5==0) t=1;
a[i]=(a[i-1]*t)%k5;
}
Int T=N; mod5=1;
while (!(T==0)){
mod5=mod5*Pow(a[k5-1],(T/k5)%phi,k5)%k5;
mod5=mod5*a[T%k5]%k5;
T=T/5;
}
mod5=mod5*Inv%k5;
return ans[mod2][mod5];
}
inline void print(long long t,int k){
if (k==1)
printf("%lld\n",t%10);
else if (k==2)
printf("%02lld\n",t%100);
else if (k==3)
printf("%03lld\n",t%1000);
}
int main(){
freopen("num.in","r",stdin);
freopen("num.out","w",stdout);
int T;
scanf("%d",&T);
while (T--){
N.read();
scanf("%d",&k);
if (N<=15){
long long t=1;
for (int i=1;Int(i)<=N;i++) t*=i;
while (t%10==0) t/=10;
print(t,k);
}else{
Pre(); print(Solve(),k);
}
}
return 0;
}
不写高精度有80分,但至今不知怎么做。


暴力分给足了的。
因为合法的顺序对应序列是唯一的,于是进行Hash,操作后如果对它所有操作的Hash值与正确的相同,那么就正确了。
所以用两个Tag的线段树维护Hash值的加法和乘法。
std写的很妙,我学习了一波。
#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
typedef unsigned int uint;
inline char nc(){
static char buf[100000],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
inline void read(int &x){
char c=nc(),b=1;
for (;!(c>='0' && c<='9');c=nc()) if (c=='-') b=-1;
for (x=0;c>='0' && c<='9';x=x*10+c-'0',c=nc()); x*=b;
}
const int N=200005;
const uint seed=233333;
struct abcd{
uint a,b;
abcd(uint a=1,uint b=0):a(a),b(b) { }
bool one() { return a==1 && b==0; }
void add(abcd B){
uint _a=a,_b=b;
a=B.a*_a; b=B.a*_b+B.b;
}
}T[N<<2];
inline void modify(int x,int l,int r,int ql,int qr,abcd t){
if (ql<=l && r<=qr){
T[x].add(t);
return;
}
if (!T[x].one())
T[x<<1].add(T[x]),T[x<<1|1].add(T[x]),T[x]=abcd();
int mid=(l+r)>>1;
if (ql<=mid) modify(x<<1,l,mid,ql,qr,t);
if (qr>mid) modify(x<<1|1,mid+1,r,ql,qr,t);
}
uint Hash[N];
inline void query(int x,int l,int r){
if (l==r){
Hash[l]=T[x].b;
return;
}
if (!T[x].one())
T[x<<1].add(T[x]),T[x<<1|1].add(T[x]),T[x]=abcd();
int mid=(l+r)>>1;
query(x<<1,l,mid);
query(x<<1|1,mid+1,r);
}
int n,K;
int main(){
int T,l,r,x;
freopen("deco.in","r",stdin);
freopen("deco.out","w",stdout);
read(n); read(K);
read(T);
while (T--){
read(l); read(r); read(x);
modify(1,1,n,l,r,abcd(seed,x));
}
query(1,1,n);
uint h=0;
for (int i=1;i<=K;i++) h=h*seed+i;
int ans=0;
for (int i=1;i<=n;i++)
if (Hash[i]==h)
ans++;
printf("%d\n",ans);
return 0;
}
用结构体存两个Tag,用构造函数运算出值。
妙啊~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号