AcWing 143. 最大异或对
AcWing 143.最大异或对
题目描述
在给定的N个整数A1,A2……AN中选出两个进行xor(异或)运算,得到的结果最大是多少?
输入格式
第一行输入一个整数N。
第二行输入N个整数A1~AN。
输出格式
输出一个整数表示答案。
数据范围
1≤N≤10^5,
0≤Ai<2^31
输入样例:
3
1 2 3
输出样例:
3
思路
先想一下暴力的做法,然后优化
int arr[N];
int ans = 0;
for(int i = 0; i < n; ++i){
for(int j = 0; j < i; ++j)
ans = (ans, arr[i] ^ arr[j]);
}
显然上述的暴力方式时间复杂度为O(n ^ 2),明显会超时,这样就要想着如何优化,这里我们可以优化内层循环:采用trie树来优化
我们每次把每一个数的二进制的没一个位存储到trie树中,这样每一个叶子节点就是代表了一个数
每输入一个x,先插入树中,我们从最高位开始与树中的数据匹配,如果存在与x在同一位置二进制位相反的数那么就选择树中的这样的点(就相当于把已经插入的数分成了两个集合...),如果不存在就选自己。如下所示
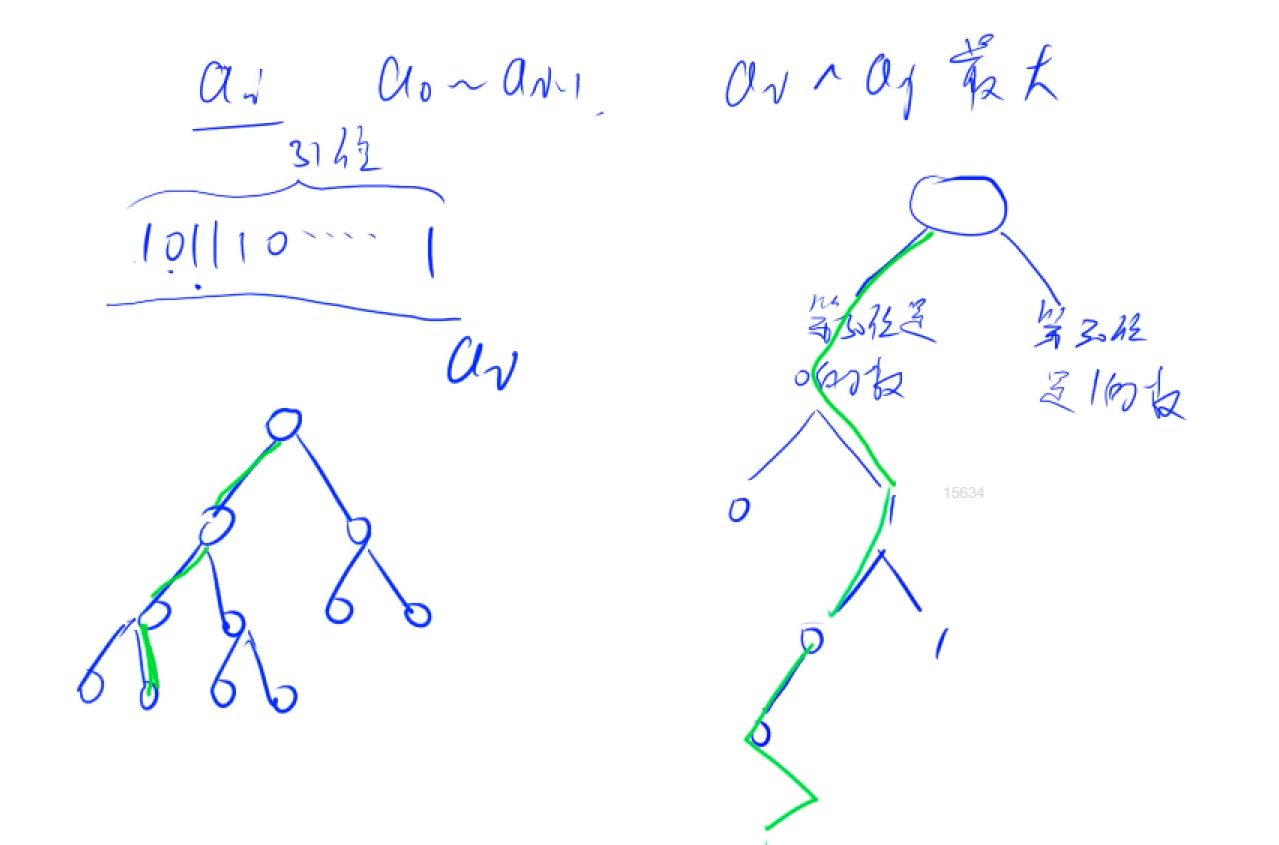
代码实现
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int s[N * 32][2], ans = 0, idx = 0;
void insert(int x){
int p = 0;
for(int i = 30; i>=0; --i){
int ch = x >> i & 1;
if(s[p][ch] == 0) s[p][ch] = ++ idx;
p = s[p][ch];
}
}
int search(int x){//当前的数和已经插入的树中的数,找异或最大值
int p = 0, ans = 0;
for(int i = 30; i >= 0; --i){
int ch = x >> i & 1;
if(s[p][!ch]){
p = s[p][!ch];
ans = ans * 2 + !ch;
}
else{
p = s[p][ch];
ans = ans * 2 + ch;
}
}
return ans;
}
int main(){
int n;cin >> n;
while(n --){
int x; cin >>x;
insert(x);
ans = max(ans, x ^ search(x));
}
cout << ans << endl;
return 0;
}
如有错误,欢迎指正!





