字符串
约定
\(S/s\) :字符串,默认从 \(1\) 编号到 \(n\)。
\(S[l,r]\):区间 \([l,r]\) 形成的子串。
\(S^R\):将字符串 \(S\) 翻转。
\(border\):公共前后缀,即 \(s[1,i] == s[j,n],n-j+1==i\)
manacher
理论
字符串算法的精髓是最大的利用之前求出的信息,这就让增量法和自动机成了字符串算法中的核心思想。
manacher 算法可以在线性时间复杂度内求出以每个点为中心的极大回文子串长度。
算法实现中我们维护:
- mid:当前最大的回文子串的中心。
- r:当前最大的回文子串的右端点。
- \(len_i\):以 \(i\) 为中心的回文半径。
考虑到回文串的长度有奇有偶,我们选择在每两个字符间插入一个无关字符,这样奇偶回文串的长度就都变成了 \(len_i - 1\)。
如果 \(i \lt r\),即 \(i\) 在当前的最大回文串的影响范围内,因为当前串是关于 \(mid\) 对称的,所以可以用 \(i\) 关于 \(mid\) 的对称点的回文半径更新 \(i\),并且要注意不能超出边界即 \(len_i = min(len_{mid * 2-i},r-i+1)\),剩下的暴力匹配即可。
因为每次 \(r\) 至少右移 \(1\),所以复杂度是线性的。
for(int i = 1; i <= n; i++){
if(i <= r) len[i] = min(r - i + 1, len[(mid << 1) - i]);
while(s[i-len[i]] == s[i+len[i]]) len[i]++;
if(i + len[i] > r){
mid = i;
r = i + len[i] - 1;
}
}
例题
最终的答案形如 \(S + pres_i^R\),满足 \(pres_i\) 为回文串,要尽量缩小 \(pres_i\) 的长度,也就是找到最靠前的回文子串满足其右端点是原串的右端点。
P3501 [POI2010] ANT-Antisymmetry
类似于正常的 manacher 过程,只不过两个字符匹配的条件变成了 xor 等于 \(1\)。
KMP
理论
定义 \(nxt_i\) 表示 \(S[1,i]\) 的最长公共前后缀,首先考虑如何快速的求出一个字符串的 \(nxt\) 数组。
考虑 DP,\(nxt_i\) 仅可以从 \(S[1,i-1]\) 的公共前后缀转移过来,找到最大的可以接上 \(S_i\) 的 \(nxt\) 这个过程可以一直跳 \(nxt\) 实现,原理如下图:
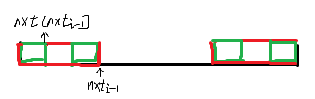
因为 \(j\) 每次最多增加 \(1\),复杂度最大的时候就是从 \(n\) 跳回 \(0\),这样是线性的。
匹配的过程和求 \(nxt\) 类似,如果当前位置失配就跳 \(nxt\),这样充分利用了一个串的信息,保证文本串的指针不会后移,所以复杂度也是线性的。
code:
for(int i = 2, j = 0; i <= n; i++){
while(j and s[j + 1] != s[i]) j = nxt[j];
if(s[j + 1] == s[i]) j++;
nxt[i] = j;
}
多项式在字符串匹配中的应用
考虑两个数相等的条件是什么 -> \(a-b = 0\),那把这个东西放到字符串上就有了代数意义上的两个字符相等的判断依据:字符的匹配函数 \(cmp(x,y) = A_x - B_y\),\(cmp(x,y) =0\) 说明 \(A_x = B_y\)。
有了这个东西后再定义一个字符串完全匹配函数:\(P(n) = \sum_{i=0}^{m-1}cmp^2(i, n-m+1+i)\),\(P(n) = 0\) 说明以 \(n\) 为结尾,字符串 A 在字符串 B 中出现。至于为什么加平方?如果不加的话会出现正负相消的情况,只要两个字符串的字符集一样两个串就匹配了,不合法呢。
为了凑出好看的形式,我们将 \(A\) 翻转并用 \(i\) 代替 \(m - i - 1\),有:
这就出来卷积式了,虽然上界比较迷,但是问题不大,直接大力出奇迹设成 \(max(n,m)\)。
这个东东还可以用来做通配符匹配:P4173 残缺的字符串
考虑通配符怎么搞?相当于强制把匹配函数的值设成零,一种方法是 \(cmp(x,y) = A_xB_y(A_x-B_y),'*' = 0\) ,这样通配符对应的匹配函数值一定是 \(0\)。推式子也和上面一样大力展开即可,这里就不写了。懒
例题
设 \(dp_{i,j}\) 表示 \([i,j]\) 的最短 \(Factoring\) 的长度,转移:\(dp_{i,j} = min(dp_{i,k},dp_{k+1,j})\),考虑一个串的压缩相当于是找出最小的周期且这个串能恰好被表示成这个周期的若干倍,以周期来代替这个串,根据一些 \(border\) 的理论,一个串的最小周期是 \(n - nxt_{n}\),直接做即可。
设 \(dp_i\) 表示覆盖完 \(i\) 的最小长度,这个值肯定不会超过 \(i\),考虑能从哪里转移,一个粗略的想法是肯定得是一个 border 才能转移,因为不是 border 的话根本不能覆盖,但是不能直接从 \(dp[nxt[i]]\) 转移,因为可能一个 \(nxt[i]\) 的长度不足以覆盖到 \(i\),所以要求 \(lst[dp[nxt[i]]] + nxt[i] \ge i\),即上一次使用长为 \(dp[nxt[i]]\) 的印章的位置接上一个 \(nxt[i]\) 能覆盖到当前位置。
似乎更像DS题
暴力 KMP 找 border,注意到 KMP 是可以在线构造的。
正解考虑在一条 border 构成的链上(失配树一条到根的路径),记录一个 \(link_{i,j}\) 表示到状态 \(i\) 的一个可以匹配上 \(j\) 的祖先,每次添加一个字符后会删掉一些border,通过 link 可以快速维护。权值考虑需要维护 添加/删除/全局取min,用一个桶存一下,暴力删除复杂度有保证,再用单调栈二分/线段树等维护下区间最值即可。
AC 自动机
理论
AC 自动机可以理解为加强版的 KMP,能解决的基本问题是多模式串匹配问题。
构建:
构造一棵 tire 树,类似 KMP 的 nxt,我们求出每个节点的失配指针 fail,失配指针的基本定义是满足是当前串(从根到当前节点的转移所形成的串)的一个最长后缀,同时又是某个串的前缀。
考虑用 DP 的思想,根据已知信息求出未知信息,如果某个串的一个前缀能匹配上当前串,并且他们的后一个字符相同,是不是就可以直接转移了?所以有 \(fail_{trans_{x,c}} = trans_{fail_x,c}\),但是如果涉及到失配跳链的话最坏是跳 \(n\) 次,所以借鉴一下并查集的路径压缩的思想,如果不存在 \(trans_{x,c}\) 令 \(trans_{x,c} = trans_{fail_x,c}\),这样失配了只需要跳一次就行了。
性质:
-
失配指针只会指向更短的串,所以失配指针构成一棵树,可以对它进行一系列树的操作。
-
fail 树上一个节点是它的子树内所有节点的后缀。
-
fail 树上如果一个节点是终止节点,那么它的子树内所有节点都是终止节点。
注意这里的终止节点可以是指存在一个模式串以它结尾或它代表一整个模式串。
-
fail 树上作为一个节点后缀出现的模式串的数量等于它到根节点的路径上代表模式串的节点数量之和
-
一个模式串在文本串中出现的次数等于他在文本串的所有前缀中作为后缀出现的次数。
根据这两个结论可以衍生出一类题目,求模式串在文本串中出现次数之和,也可以给模式串带上点权并带修,这样就变成了单点改链查,可以用树剖 \(O(n \log^2n)\) 解决。因为链查只查到根的路径,因此有一种更优秀的做法是动态树上前缀和,变成子树修改单点查询,复杂度 \(O(n\log n)\)。
code:
struct ACAM{
#define C(x) x - 'a'
int tr[MAXN][32];
int fail[MAXN], end[MAXN];
int tot;
void getfail( ){
queue<int> q;
for(int i = 0; i < 26; i++)
if(tr[0][i]) q.push(tr[0][i]);
while(!q.empty( )){
int x = q.front( ); q.pop( );
for(int i = 0; i < 26; i++){
int &y = tr[x][i];
if(y){
fail[y] = tr[fail[x]][i];
q.push(y);
}
else y = tr[fail[x]][i];
}
}
}
void insert(string s){
int now = 0;
for(char c: s){
int x = C(c);
if(!tr[now][x]) tr[now][x] = ++tot;
now = tr[now][x];
}
end[now]++;
}
} A;
例题
多模匹配的模板,拿文本串在 AC 自动机上跑,失配就跳 fail。每次累加上 fail 树上所有没有计入答案的并且代表一个完整模式串的祖先。
注意到我们压缩了 tire 树,所以可以省去跳 fail 这一步。
暴力的做法是直接拿文本串在 AC 自动机上跑,给 fail 树上所有的代表模式串的节点答案++。
根据上面的结论2,可以给每个匹配成功的节点ans++,最后答案就是子树和,同时也是二次加强版的做法。
AC 自动机上 DP 的板子,一般在 AC 自动机上 DP 都会设一个 “走了若干步到了哪个节点符合什么限制” 的状态。
先做补集转化,求不出现模式串的方案,也就是在 AC 自动机上走不到任何一个结尾节点或包含一个完整模式串的子串,根据 fail 树上 father 是当前串的后缀这一点,一个结尾节点的子树内的节点都是不合法的,设 \(dp_{i,j}\) 表示长度为 \(i\),走到了 \(j\) 节点的方案数,推表即可。
P3041 [USACO12JAN] Video Game G
AC 自动机上 DP,设 \(dp_{i,x}\) 表示走了 \(i\) 步到 \(x\) 的最大权值,转移有 \(dp_{i,x}\to dp_{i+1,trans_{x,c}}\),注意初值的设置,因为必须走到一个节点后才能用它去更新别的节点,所以初值设为 \(-\infty,dp_{0,0} = 0\)。
先建 AC 自动机没问题吧》
结论 4、5 练习题。
注意到 \(n\) 和 \(\sum_i|s_i|\) 同阶,所以长度大于 \(\sqrt n\) 的串不会超过 \(\sqrt n\) 个,可以根号分治。
对于长度大于 \(\sqrt n\) 的串直接上结论 4,暴力链加,对所有符合条件的询问贡献答案。
对于长度小于 \(\sqrt n\) 的串上结论 5,子树加并累计答案。
阈值取 \(\frac{m}{\sqrt{q\log m}}\) 最佳。
分两段考虑在文本串上枚举断点,变成求以文本串每个字符开头/结尾的模式串的个数,建两个 ACAM 分别求树上前缀和即可,答案为 \(\sum pre_{i-1}suf_i\)。
比较板,维护子树加,单点查即可。
P7456 [CERC2018] The ABCD Murderer
考虑 DP,设 \(f_i\) 为最长的以 \(i\) 结尾的模式串的长度,\(dp_i\) 表示填完前 \(i\) 个最少需要用多少个模式串。
\(f_i\) 可以 AC 自动机求得,有转移 \(dp_i = \min_{j=i-f_i}^{i-1} dp_j + 1\),数据结构维护之。
也可以倒序 DP,这样一个值能转移到的区间是固定的,可以用一个堆维护。
SAM
五年OI,三年SAM
因为笔者对这个东西也算是一知半解所以只说一些关键的东西了。
定义
SAM 是一个能接受一个字符串所有子串的最小的 DFA,状态数是 \(O(n)\) 级别的。
对于一个子串 \(s'\) ,定义 \(endpos\) 集合为:\(s'\) 在 \(s\) 中出现的所有结束位置构成的集合,根据 \(endpos\) 可以把 \(s\) 的子串分成若干等价类, \(SAM\) 上的每一个节点代表一个 \(endpos\) 等价类。
对于 SAM 上一个状态 \(p\) 给出如下定义:
\(substr(p)\): \(p\) 代表的子串集合。
\(longest(p)\): \(p\) 代表的子串的集合中最长的一个。
\(len(p)\): \(p\) 代表的所有子串中最长的一个的长度。
\(shortest(p)\):\(p\) 所代表的所有子串中最短的一个。
\(minlen(p)\):\(p\) 所代表的所有子串中最短的一个的长度。
后缀链接 \(link(p)\):从一个状态 \(p\) 指向 \(longest(p)\) 的后缀中最长的对应另一个状态的一个状态 \(w\)。 \(link\) 构成一棵树形结构,称为 parent 树。
性质与结论
- parent 树上一条从 \(p\) 到根的路径对应着一个连续的子串 \(s[1,len(p)]\)。
- SAM 上每一条从根到 \(p\) 的路径都唯一对应一个子串。
- 对于一个状态 \(q\),唯一存在转移 \((p,q)\) 使得 \(len(q) = len(p) + 1\)。
应用
- 求本质不同字串个数,由性质 2,答案为从初始状态除法的路径条数,DP 求之即可。也可以利用性质 1,一个状态里存的子串数为 \(len(p) - len(link(p))\),对所有状态求和即可。
- 求子串出现次数,考虑添加一个字符后,所有后缀的数量都会+1,也就是说一个状态代表的子串的出现次数是它子树内作为插入一个字符而添加的状态的个数,根据 parent 树的树形结构以及所有儿子的长度都比父亲长,可以通过计数排序的方法方便的统计子树和。
例题
不如暴力系列,首先套路地求出每个子串的出现次数,按字典序遍历所有子串收集答案即可。
还是处理出子串的出现次数,对一个状态 p 代表的子串 \([len_{link_p+1},len_p]\) 进行区间取 max,如果你头铁可以直接吉司机线段树,冷静一下发现 \(longest(p)\) 出现的次数一定是小于等于更短的串的,所以只需要更新 \(len(p)\) 即可,最后取后缀 max 输出。

