树分治
点分治
回想一下在序列上的二分治:每次选择序列中点,递归处理两个子序列,处理跨过两个序列的信息。前两步保证了复杂度,第三步往往是解决问题的关键,那么这个思路能不能搬到树上呢?
答案是肯定的,树分治思路和序列分治类似,我们每次递归处理子树,统计子树间的答案..,初步建立起模型后还有一个问题,如果每次我们分出的子树都极其不平均,那么总的分治次数接近 \(O(n)\),相当于没分。一个可行的解决方案是选择子树的重心作为根,因为重心的子树最大不超过 \(\frac{n}{2}\),所以可以保证 \(log\) 次的分治。
problem1
形式化题意:求树上距离不超过 \(k\) 的点对个数。
一般涉及到树上和路径相关的统计的时候点分治是一个不错的思考方向,按上面说的分治,这道题主要的矛盾点在于越过根的答案计数,下面着重解决这个问题。
考虑双指针,每次统计出所有子树中到当前根节点的距离,但是随之而来的是另一个问题——重复计数,比如这样:
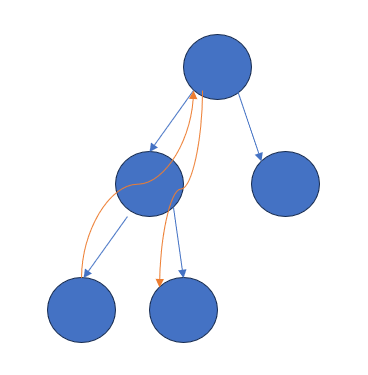
显然这是不合法的,考虑经典容斥,我们在父节点上把每颗子树的答案减去即可。
code:
点击查看代码
#include<bits/stdc++.h>
#define MAXN 1010101
#define ll long long
const int inf = 1e9 + 7;
using namespace std;
struct edge{
int u, v, w, nxt;
} e[MAXN];
int head[MAXN], cnt = 1;
int f[MAXN], vis[MAXN];
int dis[MAXN], siz[MAXN];
int root, sum;
int n, k, ans;
int tmp[MAXN], tot;
inline int read( ){
int x = 0 ; short w = 0 ; char ch = 0;
while( !isdigit(ch) ) { w|=ch=='-';ch=getchar();}
while( isdigit(ch) ) {x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return w ? -x : x;
}
inline void add( int u, int v, int w ){
e[++cnt] = (edge){ u, v, w, head[u] };
head[u] = cnt;
}
inline void getroot( int x, int fa ){
siz[x] = 1; f[x] = -inf;// 子树大小初始化,当前子树的最大子树大小初始化为零
for( int i = head[x]; i; i = e[i].nxt ){
int y = e[i].v;
if( y == fa or vis[y] ) continue;//不合法跳过,vis[y] : y是上层节点,已经作为根了
getroot( y, x );
siz[x] += siz[y];//更新子树大小
f[x] = max( f[x], siz[y] );//寻找最大的子树
}
f[x] = max( f[x], sum - siz[x] );//更新父节点
if( f[x] < f[root] ) root = x;//寻找重心
}
inline void getdis( int x, int fa ){
tmp[++tot] = dis[x];//每个节点遍历一遍, 存入临时数组
for( int i = head[x]; i; i = e[i].nxt ){
int y = e[i].v;
if( y == fa or vis[y] ) continue;//合法
dis[y] = dis[x] + e[i].w;//子节点到根结点距离 = 父节点 + 边权
getdis( y, x );
}
}
inline int deal( int x, int w ){
tot = 0;
dis[x] = w;
getdis( x, 0 );
sort( tmp + 1, tmp + tot + 1 );
int l = 1, r = tot, kkk = 0;
while( l <= r )
if( tmp[l] + tmp[r] <= k )
kkk += r - l++ ;
else r--;
return kkk;
}
inline void solve( int x ){
vis[x] = 1; ans += deal( x, 0 );//标记为根,答案无脑统计
for( int i = head[x]; i; i = e[i].nxt ){
int y = e[i].v;
if( vis[y] ) continue;
ans -= deal( y, e[i].w );//容斥多余答案
sum = siz[y];
f[0] = inf; root = 0;// 方便更新根结点
getroot( y, x );
solve( root );
}
}
int main(){
n = read( );
for( int i = 1; i < n; i++ ){
int x = read( ), y = read( ), z = read( );
add( x, y, z );
add( y, x, z );
}
k = read( );
f[0] = sum = n;
getroot( 1, 0 );//find the first root
solve( root );
cout << ans;
return 0;
}
边分治
和点分治类似,我们每次找到一条边,使得这条边两边连接的连通块大小之差最小,但是边分治也会面临和点分治一样的问题,两边的大小不平衡,比如万恶的菊花图,分治的时间复杂度极其不平衡,考虑到二叉树的优良性状,我们进行多叉转二叉。
一般来说有两种写法,一种是“左儿子右兄弟”,每个节点认领左儿子为儿子,其他的儿子都设为这个儿子的右儿子。
第二种写法是建立虚拟节点,类似线段树,对每个节点建立两个虚拟节点,把儿子分成两部分连到虚拟节点上即可。
problem2
同样的分治套路,这里仍然采用双指针写法,用两个栈维护即可。
code:
点击查看代码
#include <bits/stdc++.h>
#define AC true
#define ll long long
#define dub double
#define mar(x) for(int i = head[x]; i; i = e[i].nxt)
#define car(a) memset(a, 0, sizeof(a))
#define cap(a, b) memcpy(a, b, sizeof(b))
const int inf = 1e9 + 7;
const int MAXN = 2e5;
using namespace std;
inline int read( ){
int x = 0 ; short w = 0 ; char ch = 0;
while( !isdigit(ch) ) { w|=ch=='-';ch=getchar();}
while( isdigit(ch) ) {x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return w ? -x : x;
}
struct edge{
int u, v, w, nxt;
} e[MAXN];
struct node{
int len, val;
bool operator<(node x) const{
return val > x.val;
}
} s[2][MAXN];
#define top(op) s[op][0].val
int head[MAXN], cnt = 1;
int n, eg, seg, ans;
int val[MAXN], nn;
void add(int u, int v, int w){//y
e[++cnt] = (edge){u, v, w, head[u]};
head[u] = cnt;
e[++cnt] = (edge){v, u, w, head[v]};
head[v] = cnt;
}
vector<int> son[MAXN];
void pre(int x, int fa){//y
mar(x){
int y = e[i].v;
if(y == fa) continue;
son[x].push_back(y);
pre(y, x);
}
}
void rebuild(){//y
cnt = 1; car(head);
for(int x = 1; x <= n; x++){
if(son[x].size( ) <= 2)
for(int y: son[x]) add(x, y, y <= nn);//
else{
int s1 = ++n, s2 = ++n; val[s1] = val[s2] = val[x];
add(s1, x, 0); add(s2, x, 0);
int cur = 0;
for(int y: son[x]){
if(cur) son[s1].push_back(y);
else son[s2].push_back(y);
cur ^= 1;
}
}
}
}
int siz[MAXN];
bool vis[MAXN];
void getedge(int x, int fa, int sum){// 找重边
siz[x] = 1;
mar(x){
int y = e[i].v;
if(y == fa or vis[i >> 1]) continue;// 把 i, i^1 映射到一起
getedge(y, x, sum);
siz[x] += siz[y];
int mx = max(siz[y], sum - siz[y]);
if(mx < seg) seg = mx, eg = i;
}
}
void dfs(int x, int fa, int len, int mi, int op){
mi = min(mi, val[x]);
s[op][++top(op)] = {len, mi};
mar(x){
int y = e[i].v;
if(vis[i >> 1] or e[i].v == fa) continue;
dfs(y, x, len + e[i].w, mi, op);
}
}
void slove(int x, int sum){
seg = inf;
getedge(x, 0, sum);
if(seg == inf) return;
top(1) = top(0) = 0;
vis[eg >> 1] = 1;
dfs(e[eg].u, 0, 0, inf, 0);
dfs(e[eg].v, 0, 0, inf, 1);
sort(s[0] + 1, s[0] + top(0) + 1);
sort(s[1] + 1, s[1] + top(1) + 1);
for(int l = 1, r = 1, mx = 0; l <= top(0); l++){//
while(r <= top(1) and s[1][r].val >= s[0][l].val) mx = max(mx, s[1][r++].len);
if(r > 1) ans = max(ans, (mx + s[0][l].len + 1 + e[eg].w) * s[0][l].val);
}
for(int l = 1, r = 1, mx = 0; l <= top(1); l++){
while(r <= top(0) and s[0][r].val >= s[1][l].val) mx = max(mx, s[0][r++].len);
if(r > 1) ans = max(ans, (mx + 1 + s[1][l].len + e[eg].w) * s[1][l].val);
}
int tmp = eg;
slove(e[eg].v, siz[e[eg].v]);
slove(e[tmp].u, sum - siz[e[tmp].v]);
}
signed main( ){
nn = n = read( );
for(int i = 1; i <= n; i++) val[i] = read( );
for(int i = 1; i < n; i++){
int x = read( ), y = read( );
add(x, y, 1);
}
pre(1, 0);
rebuild( );
slove(1, n);
cout << ans;
return (0-0);
}
点分树
也叫动态淀粉质,拥有很多非常优秀的性质,支持我们把一些暴力的操作直接拿来用。
类似淀粉质的过程,我们在每层记录这一层的重心,下一层的重心向其连边,这样就形成了一棵树形结构,点分树有两个非常重要的性质:
- 树高是 \(\log n\) 级别的,是保证复杂度的基础。
- 两个节点在点分树上的的 lca 一定在原树两点间的路径上。
第二个性质是处理路径问题的关键,因为 \(dis(u,v) = dis(u,lca) + dis(v,lca)\),也就是说我们可以枚举 \(lca\) 来统计 \(u, v\) 间路径的信息(u 一般是给定的),由于我们树高是 \(\log n\) 级别的,所以这个暴力找的过程也是 \(\log n\) 级别的。
还有一个性质是点分树上每个节点的 siz 和是 \(n\log n\) 级别的,证明很简单,考虑到每个节点都会被统计 \(dep_u\) 次,树高是 \(\log n\),总和是 \(n log n\)。这个性质支持我们做一些在普通树上做不到的事,比如在每个节点上开一个 \(vector\) 之类的蛇皮操作。
problem3
题意:求距 u 不超过 k 的节点的权值和,单点修改权值。
直接淀粉质复杂度 \(O(qn\log n)\),考虑放到点分树上。对于每个节点维护两个动态开点的树状数组(其实是直接用vector存),一个维护它的子树内(点分树)到它距离不超过 k 的节点的权值和,另一个维护它的子树内到它的父亲距离不超过 k 的节点的权值和。修改直接暴力跳父亲即可,查询也是跳父亲,设当前节点是 u, 查询节点是 v,查询所有到父亲距离不超过 \(k - dis(v, fa[u])\) 的节点,剪掉 u 子树内的贡献即可。

