基础组合数学
updata1:重构全文
updata2:更新范德蒙德卷积
updata3: 更新斯特林数
updata4:更新十二重计数法并重构 \(LATEX\)
updata5:更新排版
理论
基础知识
加法原理
对于一个事情,有 n 类方法实现它,其中第 i 类有 \(m_i\) 种方法实现,那么这个事情就有 \(\sum_{i = 1}^{n}m_i\) 种实现方法。
乘法原理
对于一个事情,分为 n 个步骤完成,第 i 个步骤有 \(m_i\) 种方法实现,那么这个事情就有 \(\prod_{i = 1}^n m_i\) 种实现方法。
排列数
- 定义阶乘: \(n! = \prod_{i = 1}^{n}i\),特殊的,0! = 1
- 定义下降幂:\(n^{\underline m} = \prod_{i = n - m + 1}^{n}i\)
有 n 个彼此不同的元素,从中选出 m 个组成一个排列(顺序不同算多种)的方案数,记作 \(A_n^m\),我们有计算公式:
proof:固定 m 个位置,第一个位置有 n 种选择,第二个位置有 n - 1 种选择...第 m 个位置有 n - m + 1 种选择即 \(\prod_{i = n - m + 1}^{n}i\),可以发现这就是下降幂的定义。
据此,我们可以知道,一个数列的全排列就是 \(n^{\underline n} = n!\)
组合数
有 n 个彼此不同的元素,从中选出 m 个组成一个排列(顺序不同算一种)的方案数,记作 \(C_n^m\),我们有计算公式:
proof:组合数即为排列数除以每种组合的排列方案,总的排列方案即为全排列,所以公式显然成立。
此外,我们一般用一种更简洁的方式表示组合数:\(C_n^m = {n \choose m}\),读作“n选m”,本文将以这种方式表示组合数。
二项式系数与处理技巧
proof: 把左式拆开有: $$(a+b)(a+b)(a+b)......(a+b)$$
可以发现,\(a^i\) 相当于从这一坨里选出 \(i\) 个 \(a\),那么同时我们就选出了 \(n - i\) 个 \(b\)(一共 \(n\) 项,选了 \(a\) 就不能选 \(b\)),所以定理显然成立。
proof: n 中选 m 个 = n 中不选 n - m个。
proof:拿出一个元素,如果不选它那么就需要在剩下的 n-1 个元素中选出 m 个;如果选它就还需要在剩下的 n-1 个元素中选出 m 个。
这个公式可以用来 \(n^2\) 计算组合数,它也是杨辉三角的递推公式。
proof:把组合的计算公式展开即可。
可以用这个公式处理出一条斜线上的组合数,也可以处理一些烦人的系数。
proof:二项式定理 \(a = b = 1\) 的情况。
proof: 二项式定理 \(a = 1, b = -1\) 的情况,但是特殊地 \(n = 0\) 时值为 \(1\)。
proof: 一种显然的证明方法是直接代计算式。
另一种组合意义上的证明(Double Counting):
考虑左式相当于从 \(n\) 个元素中选出 \(i\) 个染色,再从这 \(i\) 个中选出 \(j\) 个进行染色,一共有 \(j\) 个元素被染了两遍色,\(i - j\)个元素被染了一遍色。
考虑右式相当于 \(n\) 选 \(j\) 进行两遍染色,再 \(n-j\) 选 \(i-j\) 进行一遍染色。
左式显然等于右式。
实际上是三项式系数。
多项式定理,其中 \({n \choose n_1,n_2,...,n_m}\) 是多项式系数,也叫多重组合数,实际上就是下面的多重集的排列数。
范德蒙德卷积,可以用于一些组合式子的推导。
proof1: 考虑构造函数转成二项式定理。
对应系数相等,命题得证。
\[\begin{split} \sum_{k = 0} ^{n + m} {n + m \choose k} x^k &= (x + 1)^{n + m}\\ &= (x+1)^n(x+1)^m\\ &= \sum_{k = 0}^{n} {n \choose k} x ^ k \sum_{k = 0}^{m} {m \choose k} x ^ k\\ &= \sum_{k = 0}^{m + n} x^k \sum_{i = 0} ^ k {n \choose i}{m \choose k - i} \end{split} \]proof2:
考虑组合意义上的证明,从 \(n + m\) 个小球中选出 \(k\) 个,可以把这一堆小球分成两堆,每堆的小球个数是任意的,这里认为是 \(n,m\),从第一堆中选出 \(i(0 \leq i \leq k)\) 个,就要从另一堆中选出 \(k - i\) 个,加法原理加起来就是范德蒙德卷积。
上指标求和。
proof:
多重集的排列数
- 定义多重集:一种特殊的集合,其中的元素可重,一个元素重复的次数叫做这个元素的重数。
一个多重集 \(A = \{n_1 * a_1, n_2 * a_2,...,n_k*a_k\},n = n_1 + n_2 +...+n_k\) 的全排列为:
proof:容斥轻松证,不考虑重复的情况下全排列显然是 \(n!\),第 \(i\) 个元素的排列重复了 \(n_i\) 次,排除掉即可。
容斥原理
基本形式
先上图:
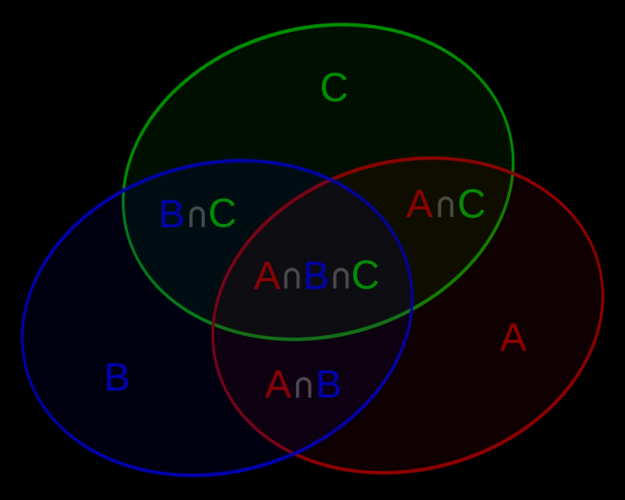
venn图可以很直观的表达出容斥原理的基本概念。
容斥原理的直观形式:
De Morgan's laws
对于全集 \(U\) 的 \(n\) 个子集,有:
简单地说就是:交集补等于补集并,并集补等于补集交。
proof:运用数学归纳法,显然得证。
杨氏矩阵 + 钩子公式
这是组合中一个非常有意思的板块。
- 定义杨氏矩阵:满足"对于矩阵中的每一个点,要么这个点没有元素,要么这个点左上方和上方的元素都小于这个点的元素"的矩阵
像这样:

值得注意的是,这里采用英式画法,还有一种法式画法,把这个表上下翻转即可。
- 定义钩子:\(H(i, j)\) 表示一个矩阵右方以及下方一共有多少个元素。
钩子公式:确定形态的杨氏矩阵共有 \(\frac{n!}{\prod H(i, j)}\) 种。
钩子公式可以用来解决“给定杨氏矩阵,问这样的矩阵一共有多少种”这类问题, 例如这道题。
这道题一个经典解法是五维dp,但是稍加思考我们可以发现,题目给出了一个杨氏矩阵,求矩阵的可能形态数显然可以钩子公式做。
鸽巢原理
又作抽屉原理。
定理内容很简单:把 \(n-1\) 个数放入 \(n\) 个盒子,一定会有一个盒子是空的。
贴一道题:
problem:
你需要维护一个数列 \(\{a_1...a_n\}\),支持两种操作(共 \(m\) 次)
- 区间每个元素取立方并对 \(v\) 取模
- 求区间是否可以选出两个非空集合使得它们内部的元素和相等
\(n, m \le 1e5,v \le 1e4\)
solution:
考虑到值域非常小,根据鸽巢原理大约 \(14\) 个元素中就一定能选出需要的两个集合。
所以询问的时候可以直接双向搜索。
修改可以建一棵线段树,维护每个数做立方操作的次数,每次查询的时候直接倍增修改即可。
插板法(隔板法)
用于解决一些 “把 \(n\) 个本质相同的元素分到 \(m\) 个本质不同的集合中” 的计数问题。
Q1:小球与盒子问题中的“球全部相同,盒子之间互不相同,每个盒子至少装一个球”问题。
考虑换一种思维方式,我们把小球放在一起,然后对他们进行分组,分组的方式就是插板,插入 \(m-1\) 个板也就分成了 \(m\) 组,一共有 \(n-1\) 个位置可以插,所以答案是 \({n-1\choose m-1}\)。
Q2:Q1 中盒子可以为空的版本。
考虑添加 \(m\) 个元素后把问题转化成 Q1,这时候答案是 \({n+m-1\choose m-1} = {n+m-1\choose n}\),这样为什么是对的呢?实际上每一个加入元素后的方案和加入前的方案构成双射,也就是一一对应的,所以对两者进行计数得到的结果是一样的。
这两个问题实际上是 \(x_1+x_2+...+x_m=n\) 的解的数量。
康托展开
求一个排列 \(P\) 的排名 \(X(P)\)(按字典序),可以写出如下公式:
其中 \(A_i\) 表示当前数列未出现的数中比 \(P_i\) 小的个数。
这个式子暴力求的复杂度是 \(O(n^2)\),可以用树状数组优化到 \(O(n\log n)\)。
proof:为什么这个式子是对的捏?可以这样想,对于一个排列中的一项 \(P_i\),它前面的项已经定死了,如果这一位填一个比 \(P_i\) 小的数,不管后面是什么排名都不会大于填 \(P_i\),而后面排列的个数是 \((n-i)!\),共有 \(A[i]\) 种填法,原式得证。
逆康托展开:把上面的式子反着算就行了,详见 oiwiki。
二项式反演
我们可以使用二项式反演解决“钦定选若干个”或“选恰好若干个”的问题。
二项式反演和多步容斥有很多相似之处,我们就从多步容斥引出二项式反演的形式零。
二项式反演·形式零
这里考虑一种特殊情况:从全集 \(U\) 中任意选出 \(k\) 个集合,他们的交集、并集大小都相等。
定义 \(f(n)\) 表示 \(n\) 个补集的交集的大小, \(g(n)\) 表示 \(n\) 个原集的交集的大小,那么根据德摩根定律:
右边这一堆可以用容斥搞:
发现这一堆就是 \(g(i)\)
反过来显然也成立,我们就得到了二项式反演的形式零。
二项式反演·形式一
proof:
考虑证明这两个定义式的互推关系,把右式代入左式。\[\begin{split} f(n) &= \sum_{i = 0} ^ n {n \choose i} \sum_{j=0}^{i} (-1)^{i-j}{i \choose j} f(j)\\ &= \sum_{i = 0} ^ n \sum_{j=0}^{i} (-1)^{i-j}{n \choose i}{i \choose j} f(j)\\ &= \sum_{i = 0} ^ n \sum_{j=0}^{i} (-1)^{i-j}{n \choose j}{n - j \choose i - j} f(j)\ \ \ \ \ \ \ \ \ (1)\\ &= \sum_{j = 0}^nf(j)\sum_{i = j}^n(-1)^{i-j}{n \choose j}{n - j \choose i - j}\\ &= \sum_{j = 0}^n{n \choose j}f(j)\sum_{k = 0}^{n-j}(-1)^{k}1^{n-j-k}{n-j \choose k}\\ &= \sum_{j = 0}^n{n \choose j}f(j) (-1+1)^{n-j}\ \ \ \ \ \ \ \ \ \ \ (2)\\ &= {n \choose n}f(n) = f(n) \end{split} \](1) 用到了组合性质6,(2)用到了二项式定理。
值得注意的是证明中并没有规定 \(i,j\) 一定从 \(0\) 开始,所以更为通用的形式一是:
二项式反演·形式二
proof:思路和过程和形式一基本一致,读者可以尝试自行证明。
二项式反演·应用*
problem1
sol:
根据题意,我们设 \(a\) 为糖果比药片能量大的组数,\(b\) 为药片能量比糖果大的组数,根据题意有:
自然解得 \(a = \frac{n+k}{2}\)。
为了方便起见,我们把糖果比与其配对的药片能量大称为满足条件。
回到题目,先把糖果排序,然后考虑dp:设 \(dp_{i,j}\) 表示钦定第 \(i\) 个满足条件,共有 \(j\) 个满足条件的方案数,\(c_i\) 表示第 \(i\) 个糖果比多少个药片能量大。
容易得到转移:
考虑二项式反演怎么做:
令 \(g(i)\) 表示“选 \(i\) 个满足条件,剩下随意的方案数”。
令 \(f(i)\) 表示“仅选 \(i\) 个满足条件的方案数”。
发现 \(g(i)\) 的前半部分就是 \(dp_{n,i}\),后半部分随意选有 \((n-i)!\) 种方案。
所以
对于 \(g(a)\),可以有 \(a, a + 1, a + 2,...,n\) 个满足条件的方案,其中每个方案中可以有 \(i \choose a\) 种选的方案,所以:
到这里就可以套二项式反演·形式二的板子了:
最后 \(f(a)\) 即为所求。
problem2:给定从左到右 \(n\) 个球,将这 \(n\) 个球用 \(k\) 种颜色染色。要求相邻两个球必须是不同的颜色,并且恰好用了 \(k\) 种颜色,问有多少种染色方案。\(n\le10^9\)。
设 \(g(i)\) 表示至多用了 \(i\) 种颜色的方案数,可以很轻易的得出
设 \(f(i)\) 表示恰好用了 \(i\) 种颜色的方案数,就有
根据二项式反演:
错排问题
现有这样一类问题:给定 \(n\) 个小球,有 \(n\) 个盒子,小球和盒子分别编号为 \(1,2,3...n\),把小球放进盒子里,要求 \(i\) 号小球不能放进 \(i\) 号盒子里,求方案数。
我们设 \(f_i\) 表示有 \(i\) 个小球的方案数,考虑 \(k_1\) 号小球放进 \(k_2\) 号盒子,\(k_2\) 号小球有两种情况:
- 放进 \(k_1\) 号盒子里
- 放进其他盒子里
对于第一种情况,很容易的发现问题的结果是 \(f_{i-2}\)。
对于第二种情况,我们强制 \(k_2\) 号小球不能放进 \(k_1\) 号盒子里,发现问题相当于把 \(k_1\) 号小球和 \(k_1\) 号盒子踢走,结果是 \(f_{i-1}\)。
回到最开始,我们假定的 \(k_1\) 和 \(k_2\) 都是任意的,所以每个数可以和其余 \(i -1\) 个数“配对”,最终的递推式是:
此外,我们还可以用二项式反演解决这个问题,设 \(g(i)\) 表示至多有 \(i\) 个数构成了错排,那么这 \(i\) 个数所有的排列方案都满足 \(g(i)\) 的性质,所以
设 \(f(i)\) 表示恰好有 \(i\) 个数构成错排的方案数,有:
根据二项式反演:
把这个式子拆开看看:
这就是所谓的全错排公式。
斯特林数
- 定义 \(n \brack m\) 为第一类斯特林数,表示 \(n\) 个带标号元素分为 \(m\) 个非空无标号圆排列的方案数。
- 定义 \(n \brace m\) 为第二类斯特林数,表示 \(n\) 个带标号元素分为 \(m\) 个非空无标集合的方案数。
第二类斯特林数
有一个简单的递推式:
proof:考虑第 \(1\) 个小球是不是被放进一个单独的盒子里,如果是的话,因为盒子都一样,方案数就是 \({n - 1 \brace m - 1}\),如果不是,那么就有 \(m\) 个盒子可以选择,方案数就是 \(m \times {n - 1 \brace m}\)。
更优秀的做法是二项式反演,可以求出通项公式:
设 \(f(n,m)\) 表示 \(n\) 个不同球放入 \(m\) 个不同盒子,每个盒子至少装一个球的方案数,容易发现第二类斯特林数其实就是 \(\frac{f(n,m)}{m!}\)。
求 \(f(n,m)\) 就直接二项式反演搞过来:
令 \(g(n,m)\) 表示 \(n\) 个不同球放进 \(m\) 个不同盒子,盒子可空的方案数,容易发现\(g(n,m) = m^n\)。
所以
性质:
proof:左式为 \(n\) 个不同球放进 \(m\) 个不同盒子,盒子可空的方案数,考虑右式,从组合的意义上理解就是,选出 \(i\) 个盒子非空, \({n \brace i} \times i!\) 是不同盒不同球的,乘上选出的非空盒子数就是左式。
按行求:
观察上面二项式反演的结果,很容易发现这是个卷积的形式,直接做即可。
按列求:
我们先假设盒子带标号,设盒子带标号 \(n \brace 1\) 的 \(EGF\) 为 \(G\),显然无论 \(n\) 取何值只有一种方案,\(G = \sum_{i=1}\frac{x^i}{i!} = e^x-1\),那么盒子带标号 \(n \brace k\) 的 \(EGF\) 即为 \(G^k\)。
因为强制赋了标号,需要除去影响,最后 \(k!\sum_{i} \frac{{i \brace k}x^i}{i!} = G^k\),做一个多项式快速幂即可,注意这里首项可能是 \(0\),所以需要特殊处理。
第一类斯特林数
还是递推式:
proof:同第二类,考虑新加入一个元素,可以塞在任何一个轮换的任何一个元素后面,也可以塞进一个新的轮换里。
按列求:
同上,考虑给轮换标号,设单个轮换的 \(EGF\) 为 \(G\),那么 \(G = \sum_{i=1}\frac{(i-1)!x^i}{i!} = \sum_{i = 1}\frac{x^i}{i}\)
\(k\) 个轮换的 \(EGF\) 就是 \(G^k\),所以
直接求即可。
按行求:
设同一行的第一类斯特林数的 \(OGF\) 为 \(F_n = \sum_{i} {n \brack i} x^i\)。
根据递推式有 \(F_n = (n-1)F_{n-1} + xF_{n-1}\),解出来是 \(F_n = \frac{(x+n-1)!}{(x-1)!} = x^{\overline n}\)
可以直接分NTT,复杂度 \(O(n\ \log^2n)\)。
其实可以继续推一下,记 \(f(x) = x^{\overline n}\) ,考虑到 \(x^{\overline{2n}} = x^{\overline n}(x + n)^{\overline n}\),那么只需要想办法求出 \(f(x+n)\) 就可以倍增做了。
已经可以看出卷积形式了,令 \(A(x) = \sum f[i]i!,B(x) = \sum \frac{k^i}{i!}\)
直接做卷积,倍增即可。
上升幂/下降幂多项式转普通幂多项式
上升幂转普通幂:\(x^{\overline n} = \sum_{i}{n \brack i} x^i\)
普通幂转上升幂:\(x^n = \sum_i{n \brace i} (-1)^{n-i}x^{\overline i}\)
下降幂转普通幂:\(x^{\underline n} = \sum_i{n \brack i} (-1)^{n - i}x^i\)
普通幂转下降幂:\(x^n = \sum_i{n \brace i} x^{\underline i}\)
斯特林反演
一个好玩的性质:
例题
十二重计数法
sol1:
因为没有限制,所以每个小球都可以放进 \(m\) 个盒子里,一共有 \(n\) 个小球,根据乘法原理,\(ans = m^n\)。
sol2:
因为每个盒子最多装一个球,所以考虑把盒子固定,相当于从 \(n\) 个小球中选出 \(m\) 个小球,并且盒子互不相同,所以构成一个排列,容易发现这就是排列数的定义,所以 \(ans = n^{\underline m}\)。
sol3:
考虑第二类斯特林数,这里要求盒子不同所以直接乘上 \(m!\) 即可。
最后 \(ans = m! \times {n \brace m}\)。
sol4:
球不同盒相同考虑第二类斯特林数,和板子不同,这里要求盒子可空,很显然,我们可以枚举有多少个盒子不是空的,所以最后 \(ans = \sum_{i = 0}^m{n \brace i}\)。
sol5:
如果球比盒子多的话根本装不满,方案数是 \(0\),否则把所有球都放进去,因为盒子都是一样的,所以方案数是 \(1\)。\(ans = [n \leq m]\)。
sol6:
很显然是第二类斯特林数的定义,\(ans = {n \brace m}\)。
sol7:
考虑插板法,这里有了空盒的限制,考虑最开始向每个盒子中放一个球,这样就转化成了我们熟知的“盒子非空”问题,最后再把多放的球拿走,就结了。\(ans = {n + m - 1 \choose m - 1}\)。
sol8:
如果盒子比球少肯定不可行,否则问题就变成了“\(m\) 个不同的盒子中选出 \(n\) 个装球”的方案数,发现这就是组合数的定义,\(ans = {m \choose n}\)
sol9:
基本的插板法,\(ans = {n-1\choose m-1}\)。
sol10:
这里有一个转化,把原问题放到网格图上,横轴代表每个盒子,纵轴代表放的球数,最终结果就是从 \((0,0)\) 走到 \((n,m)\) 的阶梯形的面积是恰好是 \(n\) 的方案数,为什么可以这样转化捏?因为我们求的是盒子无序的方案数并且所有的盒子之间都是相同的,那我们不妨给盒子定一个“顺序”,求得这种顺序下的方案数就是总的方案数。
回到这个模型上,我们可以很轻易的得出 dp 的转移方程:\(f_{i,j} = f_{i-j,j}+f_{i,j-1}\),含义就是向上走一步需要在右面每个盒子里填 \(j\) 个球,向右走一步就相当于再拿出一个盒子。
我们借助生成函数,尝试把这个式子化的优美一些,仔细观察这个式子,我们如果要用生成函数表示的话,表示 \(j\) 这一维无疑是更好的,因为这一维有相当好的递推形式,求解递归式就会容易很多。
设 \(F_k = \sum_{i=1}^{\infty}f_{i,k}x^i\),那么就有:
这样就可以一步到位的解出我们要的式子了:
接下来是怎么算这个东西,有一个题叫 付公主的背包 就是求这个式子的其实就是 Euler 变换,考虑到直接求的复杂度是 \(O(n^2\log n)\) 的,那不难想到取 \(ln\) 转点值加,最后再 \(exp\) 回去,所以:
这么一看好像没什么用,但是别急,我们有结论:
具体证明不会可以参考别的 dalao 的题解,这里就直接用了,我们枚举每个 \(i\) 贡献到对应的系数上,最后 \(Exp\) 回去即可,答案是 \(F_m\) 的第 \(n\) 项系数。
sol11:
理同 sol5,\(ans = [n\leq m]\)。
sol12:
理同 sol10,只不过变成了取 \(n-m\) 项的系数。

