LCA四法

说在前面

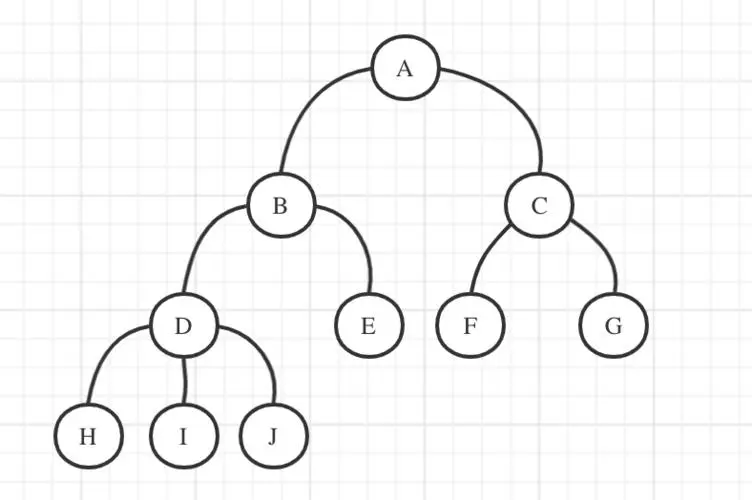
image
全文基于这张图。

朴素算法（向上标记法）

LCA问题，即求树上两点间的最近公共祖先。
最朴素的算法是把要求的两个点先跳到同一深度，然后不断的向父亲跳，直到两个节点相遇。
实现细节举个例子说，I 和 F 两个节点，I 深度大，向上跳到 D，现在深度一样，同时跳父亲，D->B,F->C，不是同一个节点，继续跳，B->A，C->A，跳到同一个节点，LCA 就是 A。
朴素算法在随机树上的单次查询时间复杂度是 O(logn)，但是在诸如链上的特殊数据上会退化为 O(n)。

倍增

相当于对朴素算法的优化。可以发现朴素算法的时间复杂度主要受限于向上跳的过程，考虑通过倍增算法对这个过程进行优化。
先处理出来每个节点的 2k(k<32) 级祖先，之后向上跳的过程都可以直接跳祖先来优化。
具体的实现有几个细节：
处理一个节点的祖先的时候可以通过一个显而易见的递推来处理，fax,i 代表节点 x 的第 2i 级祖先，递推式是 fa[x][i] = fa[fa[x][i-1]][i-1]。
之后就是基本的倍增了，注意在代码实现的时候不会正好跳到 LCA 上，而是跳到 LCA 的子节点上，因为代码实现的时候会判断两个节点跳祖先之后不会相遇才继续跳，可以看下面的例子。
例子还是 I 和 F：
先调整到同一深度，I -> D(20级祖先)，之后一起跳祖先， 发现只有 20 级祖先不相同，跳，D -> B, F -> C，最后 LCA 就是 B 或者 C 的父亲。
时间复杂度是预处理 O(nlogn) + 单次查询 O(logn)

ST表

ST表做法的基础是树的欧拉序列，一棵树的欧拉序列定义为对一棵树进行 DFS，无论是第一次遇到还是回溯都把这个节点的编号记录下来，最后会形成的一个长为 2n−1 的序列。
上图的欧拉序列为：ABDHDIDJDBEBACFCGCA。
这里定义 pos(i) 为某个节点在欧拉序列中第一次出现的位置。
欧拉序列有一个很好的性质，节点 i 和 j 的 LCA 一定出现在欧拉序列上 pos(i) 和 pos(j) 之间，而且这两个位置之间不会出现 LCA(i,j) 的祖先。这也就意味着在欧拉序列上 pos(i) 和 pos(j) 之间编号最小的节点就是 LCA(i,j)。问题转化成了一个 RMQ 问题，可以采用 ST 表实现。
时间复杂度是预处理 O(nlogn) + 单次查询 O(1)。
但是事实上我们有更好用的 dfs 序 + ST 表，具体可以参考 冷门科技 —— dfs 序求 LCA

tarjan

tarjan算法是一种离线求 LCA 的算法，从宏观上讲，tarjan是从子树的角度处理的LCA。和倍增算法不同，tarjan在读入阶段将需要求 LCA 的节点对储存在对应的节点上，在遍历树的过程中，通过并查集维护节点之间的父子关系。
对于一个有询问的节点，遍历他的所有询问，如果某个询问的另一个节点已经回溯过了，那么一直用并查集 get 这个节点的 father，最后得到的就是 LCA。
至于为什么这个算法可以实现，我们可以这样想，我们在遍历一棵树的时候，一定是先遍历两个节点的 LCA 再遍历这两个节点，如果一个节点已经被遍历过了，那么这时候一直get father 都会得到 LCA，因为并查集最开始的初始化是初始化成节点本身，只有在回溯的时候才会更新 father 成他的父亲。
还有一个问题是，vis标记的究竟是是否回溯过还是是否遍历过，其实这两种方案并没有效果上的区别，分两种情况讨论一下，如果两个节点之间是没有祖先关系（比如上图中的 I 和 F），那么这两种方法是没有区别的，如果有父子关系的话（比如 I 和 B），那么标记是否回溯过的方法会在深度较小的一个节点处统计答案（从深度较大的节点处一直getfather），标记是否遍历过的方法会在深度较大的节点处统计答案（（从深度较小的节点处一直getfather），仔细考虑一下这两种方案，其实是一样的，最终getfather得到的答案都是 LCA，所以这两种标记方案其实没有效果上的区别。
还是拿这张图举例子：
（这里用id代指询问编号）
假设有 (D,B) (I,E) (H,F) 三组询问，读入的时候在这几个节点上记录询问。
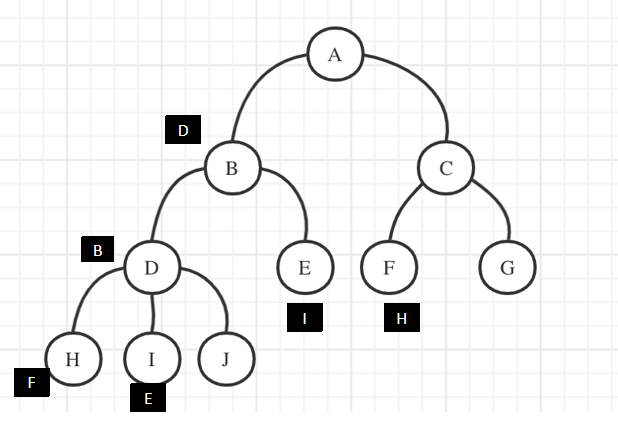
image
开始遍历到 B，发现 D 没有遍历过，继续遍历。
遍历到 D，发现 B 遍历过了，更新 ans[id] = get(B) = B。
继续遍历到 H，发现 F 没有遍历过，回溯，更新 fa[H] = D。
继续重复此过程，过程中完成更新 fa[I] = D, fa[J] = D, fa[D] = B。
遍历到 E，发现节点 I 遍历过，更新 ans[id] = get(I) = B。
继续重复，直到遍历到 F，更新 ans[id] = get(H) = A。
完成遍历，输出答案。
tarjan 算法求 LCA 的时间复杂度是 询问+处理 O(n) 的，但是离线。

树链剖分

基础树剖就不讲了。树剖求 LCA 其实也是对朴素算法的优化，只需要把跳父亲的过程用跳链顶优化即可。
时间复杂度 预处理 O(n) + 单次询问 O(logn)，但是常数极小，在不特意卡树剖并且询问不多的情况下比 O(1) 要快，这里推荐日常用。

代码实现

以luogu模板为例。

倍增：

点击查看代码 
#include <bits/stdc++.h>

#define ll long long
#define MAXN 1010101

using namespace std;

struct edge{ int u, v, nxt; }e[MAXN];
int head[MAXN], cnt;
int n, m, s;
int f[MAXN][20], dep[MAXN];
int lg[MAXN];

void add( int x, int y ){
    e[++cnt] = (edge){ x, y, head[x] };
    head[x] = cnt;
}

void mylog( ){
    for( int i = 1; i <= n; i++ )   
        lg[i] = lg[i-1] + ( 1 << lg[i-1] == i );
    return;
}

void dfs( int x, int fa ){
    f[x][0] = fa;
    dep[x] = dep[fa] + 1;

    for( int i = 1; i <= lg[dep[x]]; i++ )
        f[x][i] = f[f[x][i-1]][i-1];

    for( int i = head[x]; i; i = e[i].nxt ){
        int y = e[i].v;
        if( y != fa ) dfs( y, x );
    }
    return;
}

int lca( int x, int y ){
    if( dep[x] > dep[y] ) swap( x, y );
    for( int i = 20; i >= 0; i-- )//调整到同一深度
        if( dep[x] <= dep[y] - ( 1 <<  i ) ) y = f[y][i];
    if( x == y ) return x; // x是y的祖先
    for( int i = lg[dep[x]] - 1; i >= 0; i-- )
        if( f[x][i] != f[y][i] ) x = f[x][i], y = f[y][i];
    return f[x][0];
}

int main( ){

    scanf("%d%d%d",&n,&m,&s);

    mylog( );

    for( int i = 1; i <= n - 1; i++ ){
        int x, y; scanf("%d%d",&x,&y);
        add( x, y ); add( y, x );
    }

    dfs( s, 0 );

    for( int i = 1; i <= m; i++ ){
        int a, b; scanf("%d%d",&a,&b);
        printf("%d\n",lca( a, b ));
    }

    return 0;
}

ST表：

点击查看代码 
#include <bits/stdc++.h>

#define ll long long
const int inf = 1e9 + 7;
const int MAXN = 5e5 + 10;

using namespace std;

struct edge{
	int u, v, nxt;
} e[MAXN << 1];
int head[MAXN], cnt = 1;
int dfn[MAXN], tot;
int lg[MAXN], dep[MAXN];
int st[MAXN][25];
int n, q, rt;

inline int read( ){
    int x = 0 ; short w = 0 ; char ch = 0;
    while( !isdigit(ch) ) { w|=ch=='-';ch=getchar();}
    while( isdigit(ch) ) {x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
    return w ? -x : x;
}

void add(int u, int v){
	e[++cnt] = (edge){u, v, head[u]};
	head[u] = cnt;
}

int cmp(int x, int y){return dep[x] < dep[y] ? x : y;}

void dfs(int x, int f){
	dfn[x] = ++tot;
	st[tot][0] = f;
	dep[x] = dep[f] + 1;
	for(int i = head[x]; i; i = e[i].nxt){
		int y = e[i].v;
		if(y == f) continue;
		dfs(y, x);
	}
}

int get(int x, int y){
	if(x == y) return x;
	x = dfn[x]; y = dfn[y];
	if(x > y) swap(x, y);
	int k = lg[y - x];
	x++;
	return cmp(st[x][k], st[y - (1 << k) + 1][k]);
}

signed main( ){
	
	n = read( ); q = read( ), rt = read( );

	for( int i = 2; i <= n; i++ )
        lg[i] = lg[i >> 1] + 1;

	for(int i = 1; i < n; i++){
		int u = read( ), v = read( );
		add(u, v); add(v, u);
	}
	
	dfs(rt, 0);
	
	for(int j = 1; j <= 20; j++)
		for(int i = 1; i + (1 << j) - 1 <= n; i++)
			st[i][j] = cmp(st[i][j-1], st[i+(1 << (j - 1))][j-1]);
	
	for(int i = 1; i <= q; i++){
		int x = read( ), y = read( );
		cout << get(x, y) << endl;
	}

	
	return 0;
}
tarjan：
点击查看代码 
#include <bits/stdc++.h>

#define ll long long
const int inf = 1e9 + 7;
const int MAXN = 5e5 + 10;

using namespace std;

struct node{int v, id;};
struct edge{
	int u, v, nxt;
} e[MAXN << 1];
int head[MAXN], cnt = 1;
vector <node> u[MAXN];
int n, q, rt;
int fa[MAXN], vis[MAXN];
int ans[MAXN];

inline int read( ){
    int x = 0 ; short w = 0 ; char ch = 0;
    while( !isdigit(ch) ) { w|=ch=='-';ch=getchar();}
    while( isdigit(ch) ) {x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
    return w ? -x : x;
}

void add(int u, int v){
	e[++cnt] = (edge){u, v, head[u]};
	head[u] = cnt;
}
int get(int x){return x == fa[x] ? x : fa[x] = get(fa[x]);}

void tarjan(int x, int f){
	vis[x] = 1;
	for(int i = head[x]; i; i = e[i].nxt){
		int y = e[i].v;
		if(y == f) continue;
		if(!vis[y]) tarjan(y, x), fa[y] = fa[x];
	}
	for(int i = 0; i < (int)u[x].size( ); i++)
		if(vis[u[x][i].v]) ans[u[x][i].id] = get(u[x][i].v);
}

signed main( ){
	
	n = read( ); q = read( ), rt = read( );
	
	for(int i = 1; i <= n; i++)
		fa[i] = i;
	for(int i = 1; i < n; i++){
		int u = read( ), v = read( );
		add(u, v); add(v, u);
	}
	for(int i = 1; i <= q; i++){
		int x = read( ), y = read( );
		u[x].push_back((node){y, i});
		u[y].push_back((node){x, i});
	}
	
	tarjan(rt, 0);
	
	for(int i = 1; i <= q; i++)
		cout << ans[i] << endl;
	
	return 0;
}

树剖：

点击查看代码 
#include <bits/stdc++.h>

#define ll long long
const int inf = 1e9 + 7;
const int MAXN = 5e5 + 10;

using namespace std;

struct edge{
	int u, v, nxt;
} e[MAXN << 1];
int head[MAXN], cnt = 1;
int n, q, rt;
int siz[MAXN], son[MAXN];
int top[MAXN], fa[MAXN];
int dep[MAXN];

inline int read( ){
    int x = 0 ; short w = 0 ; char ch = 0;
    while( !isdigit(ch) ) { w|=ch=='-';ch=getchar();}
    while( isdigit(ch) ) {x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
    return w ? -x : x;
}

void add(int u, int v){
	e[++cnt] = (edge){u, v, head[u]};
	head[u] = cnt;
}

void dfs1(int x, int f){
	siz[x] = 1; fa[x] = f;
	dep[x] = dep[f] + 1;
	for(int i = head[x]; i; i = e[i].nxt){
		int y = e[i].v;
		if(y == f) continue;
		dfs1(y, x);
		siz[x] += siz[y];
		if(siz[y] > siz[son[x]]) son[x] = y;
	}
}
void dfs2(int x, int tp){
	top[x] = tp;
	if(son[x]) dfs2(son[x], tp);
	else return;
	for(int i = head[x]; i; i = e[i].nxt){
		int y = e[i].v;
		if(y == fa[x] or y == son[x]) continue;
		dfs2(y, y);
	}
}

int lca(int x, int y){
	while(top[x] != top[y])
		if(dep[top[x]] > dep[top[y]]) x = fa[top[x]];
		else y = fa[top[y]];
	return dep[x] < dep[y] ? x : y;
}

signed main( ){
	
	n = read( ); q = read( ), rt = read( );

	for(int i = 1; i < n; i++){
		int u = read( ), v = read( );
		add(u, v); add(v, u);
	}
	
	dfs1(rt, 0);
	dfs2(rt, rt);
	
	for(int i = 1; i <= q; i++){
		int x = read( ), y = read( );
		printf("%d\n",lca(x, y));
	}

	
	return 0;
}
posted @   Kun_9  阅读(90)  评论(0)  编辑  收藏  举报
相关博文：
·  时空复杂度分析与主定理
·  luoguP3403跳楼机 题解【同余最短路】
·  LCA（最近公共祖先）
·  学习笔记：最近公共祖先
·  图论专题-学习笔记：最近公共祖先 LCA
阅读排行：
· 地球OL攻略 —— 某应届生求职总结
· 周边上新：园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源！
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】
点击右上角即可分享
微信分享提示
SQL AI 助手