网络流概述
uptada 2023/11/7：局部重构。
算法
基础概念：
- 网络 : 一张有向图，其中每个边都有一个边权，被称为容量
- 流：可以类比水流，从源点流出流入汇点
- 源点和汇点：所有流流出的节点(S)和所有流流入的节点(T)
- 对于一条边 \((x,y)\) 我们称 \(f(x,y)\) 为它的流量, 称 \(c(x,y)\) 为它的容量,称 \(c(x,y)-f(x,y)\) 为它的残余容量
注意这里 流量 \(\neq\) 容量
网络中的每一条边满足以下三条限制：
-
\(f(x,y) \le c(x,y)\)
即经过一条边的流量不超过它的容量，即容量限制。
-
\(f(x,y) = -f(y,x)\)
一条边的流量与其反向边的流量之和为0，即斜对称性。
-
\(\forall \ x \in V,x\neq S,x\neq T, \sum _( \ _u \ _ , \ _ x \ _ ) \ _ \in \ _ E \ f(u,x) = \sum _( \ _x \ _ , \ _ v \ _ ) \ _ \in \ _ E \ f(x,v)\)
一个点总流入的流量 = 总流出的流量，即流量守恒。
一般来说我们认为源点流出的流是无限的。
EK算法
前置概念
- 增广路：一条从源点到汇点的路径，其所有边的残余容量都非负
- 残余网络：在任意时刻，网络中的所有节点和残余容量大于零的边构成的子图
解决最大流问题的一个基本做法是不断寻找增广路，这里不加证明的给出结论
增广路算法总能找到一张网络的最大流。
朴素的 dfs 实现是 FF 算法，复杂度和容量相关，而基于 bfs 增广的 EK 算法有着更优秀的复杂度。
算法原理
EK 的思想是朴素的：首先，找到一条从源点到汇点流量为 0 的路径一定是可行的，之后再把这条路径上的流量加大到不能加为止就找到了一条增广路，只要不断地寻找增广路就能找到最大流。
如果你模拟一下这个过程就会发现，这样做正确性似乎有些问题，比如下面这张图
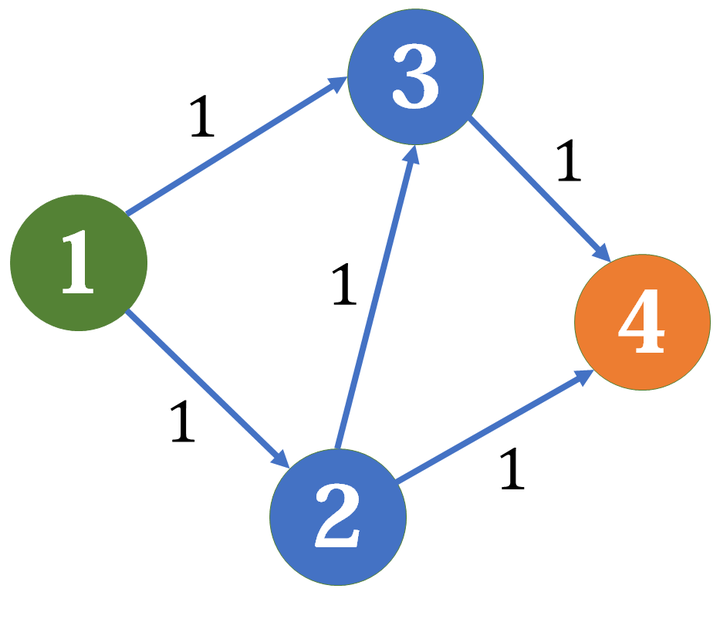
如果选择 1 -> 2 -> 3 -> 4 进行增广得到的最大流为 1
但是最大流显然是通过 (1 -> 3 -> 4) + (1 -> 2 -> 4) 得到的 2
为了解决这个问题，我们引入反向边的概念，给程序一个反悔的机会，具体来说，流经一条边和其反向边相当于并未流经这一条边。
反向边，顾名思义就是在每条正向边所连接的两个节点之间连一条相反的，边权为零的边，根据斜对称性，在每条边流过大小为 f 的流量时（表现在代码中就是边权减去 f），其反向边容量应该加上 f。
为了方便寻找反向边，我们采用成对变换的技巧，即把两点间的两条边存在 a 和 a+1 处，则 e[i] 和 e[i^1] 就表示两条边。
算法流程
- 找到一条增广路
- 找到这条增广路上的最小容量
- 增加最大流
- 重复第一步直到源点和汇点不连通
最后放上代码
点击查看代码
inline bool bfs( ){
memset( inq, 0, sizeof( inq ) );
while( !q.empty( ) ) q.pop( );
q.push( s ); inq[s] = 1;
while( !q.empty( ) ){
int x = q.front( ); q.pop( );
for( int i = head[x]; i; i = e[i].nxt ){
int y = e[i].v;
if( inq[y] or !e[i].w ) continue;
pre[y].v = x;
pre[y].e = i;
if( y == t ) return 1;
inq[y] = 1;
q.push( y );
}
}
return 0;
}
inline int EK( ){
int ans = 0;
while( bfs( ) ){
int mi = inf;
for( int i = t; i != s; i = pre[i].v )
mi = min( mi, e[pre[i].e].w );
for( int i = t; i != s; i = pre[i].v ){
int x = pre[i].e;
e[x].w -= mi;
e[x^1].w += mi;
}
ans += mi;
}
return ans;
}
EK算法时间复杂度上界是 \(O(nm^2)\) 的，虽然网络流算法运行时间很玄学能跑过 1e3~1e4 的数据，但我们需要更快。
dinic算法
在下面这张图中，EK算法暴露出一个致命的问题
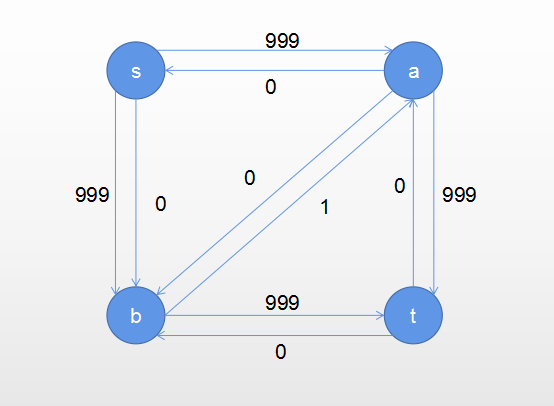
如果选择了 s->a->b->t 这条路径那么EK算法需要执行大量不必要的操作，运行时间直接爆炸，这是我们不能容忍的。
所以就需要请出 dinic 算法，一般来说在 oi 中大部分的网络流问题都是采用 dinic 解决的。国际法规定不能卡dinic。
算法原理
首先在残余网络上建立分层图（注意不是最短路的分层图），即对于一条边 \((x,y)\) ，都有 y 的层次d[y] = d[x] + 1，每次增广的时候只走下一层的节点。实际上相当于把 EK 中的 dfs 增广换成了 bfs 增广，一次可以增广多条增广路。
算法流程
- 首先通过bfs对残余网络进行分层
- 然后寻找增广路并更新残余网络
- 最后累加最大流
放代码（无优化）
点击查看代码
bool bfs( ){
while( !q.empty( ) ) q.pop( );
for( int i = 1; i <= (n << 2); i++ ){
dis[i] = 0;
}
dis[s] = 1;
q.push( s );
while( !q.empty( ) ){
int x = q.front( ); q.pop( );
for( int i = head[x]; i; i = e[i].nxt ){
int y = e[i].v;
if( dis[y] or !e[i].w ) continue;
dis[y] = dis[x] + 1;
q.push( y );
}
}
if( dis[t] ) return 1;
return 0;
}
int dfs( int x, int low ){
int rlow = 0, used = 0;
if( x == t ){
ans += low;
return low;
}
for( int i = head[x]; i; i = e[i].nxt ){
int y = e[i].v;
if( dis[y] == dis[x] + 1 and e[i].w ){
rlow = dfs( y, min( low - used, e[i].w ) );
if( rlow ){
used += rlow;
e[i].w -= rlow;
e[i^1].w += rlow;
if( used == low ) break;
}
}
}
return used;
}
void dinic( ){
while( bfs( ) ){
dfs( s, inf );
}
}
这里直接在 dfs 中累加了最大流。
dinic 还有一个非常有用的优化，当前弧优化，通过它可以不访问那些不可能到达汇点的边，从而大大加快算法效率。
代码也很简单，只需要在代码里加上两行
for( int i = 1; i <= (n << 2); i++ ) cur[i] = head[i];
for( int &i = cur[x]; i; i = e[i].nxt )
完整代码如下
点击查看代码
bool bfs( ){
while( !q.empty( ) ) q.pop( );
for( int i = 1; i <= (n << 2); i++ ){
cur[i] = head[i];
dis[i] = 0;
}
dis[s] = 1;
q.push( s );
while( !q.empty( ) ){
int x = q.front( ); q.pop( );
for( int i = head[x]; i; i = e[i].nxt ){
int y = e[i].v;
if( dis[y] or !e[i].w ) continue;
dis[y] = dis[x] + 1;
q.push( y );
}
}
if( dis[t] ) return 1;
return 0;
}
int dfs( int x, int low ){
int rlow = 0, used = 0;
if( x == t ){
ans += low;
return low;
}
for( int &i = cur[x]; i; i = e[i].nxt ){
int y = e[i].v;
if( dis[y] == dis[x] + 1 and e[i].w ){
rlow = dfs( y, min( low - used, e[i].w ) );
if( rlow ){
used += rlow;
e[i].w -= rlow;
e[i^1].w += rlow;
if( used == low ) break;
}
}
}
return used;
}
void dinic( ){
while( bfs( ) ){
dfs( s, inf );
}
}
}
dinic算法时间复杂度是\(O(n^2m)\)，可以胜任大多数最大流题目了。
费用流
现在给每个边加上一维费用表示每单位的流量会产生这么多的代价，要求求出最小费用/最大费用最大流。
只需要把最大流中的 bfs 换成 spfa 即可。
点击查看代码
namespace mcmf{
const int N = 2e4 + 10;
struct edge{
int u, v, f, w, nxt;
} e[N];
int head[N], cnt = 1;
int s, t, cst, fl;
int flow[N], pre[N], dis[N], inq[N], prew[N];
void add(int u, int v, int f, int w){
e[++cnt] = (edge){u, v, f, w, head[u]};
head[u] = cnt;
e[++cnt] = (edge){v, u, 0, -w, head[v]};
head[v] = cnt;
}
queue<int> q;
bool spfa( ){
memset(dis, 0x3f, sizeof(dis));
flow[s] = inf; dis[s] = 0; pre[t] = -1;
q.push(s); inq[s] = 1;
while(!q.empty( )){
int x = q.front( ); q.pop( ); inq[x] = 0;
for(int i = head[x]; i; i = e[i].nxt){
int y = e[i].v;
if(dis[x] + e[i].w < dis[y] and e[i].f){
dis[y] = dis[x] + e[i].w;
pre[y] = x; prew[y] = i;
flow[y] = min(flow[x], e[i].f);
if(!inq[y]) q.push(y), inq[y] = 1;
}
}
}
return pre[t] != -1;
}
int EK( ){
cst = fl = 0;
while(spfa( )){
int now = t;
fl += flow[now];
cst += dis[now] * flow[now];
while(now != s){
e[prew[now]].f -= flow[t];
e[prew[now] ^ 1].f += flow[t];
now = pre[now];
}
}
return cst;
}
};
最小割
求选出一个边集使得源汇不连通的总权值和最小的边集，有一个非常重要的定理是最大流等于最小割。
证明很简单，如果你会线性规划的话你会发现最大流和最小割实际上是对偶问题，从残量网络上来理解的话，最终的残量网络上源汇是不连通的，而这时候求出的最大流就刚好对应使得源汇不连通的边权和。
建模
网络流的题目大多都是考察建模能力的，上面的算法熟练掌握板子就差不多了。
problem1 【练手题】
对每个人和座位分别建点,源点连向每个人，每个人连向他们想要的座位，每个座位连向汇点，边权为2，因为每个座位上可以坐两个人。
problem2【三分图匹配】
考虑限制，每个人可以选择 文/理，可以考虑用二分图，选特定集合的人有额外收益，考虑新建一个节点表示选择这个节点相连的所有节点。
最终建图：每个点拆成两个表示文理，源点向文连边，汇点向理连边，容量为选文/理的价值，文理之间连inf，源点连向虚拟节点连边，容量为same，虚拟节点向对应的相邻节点连边，容量为 inf，汇点同理。
这样割断了源点和对应节点的边代表放弃了选文的收益，如果要获得相邻的人全选文的收益就要割掉所有选理的边，也可以直接放弃这个收益。
problem3【最小边数最小割】
题意是求边数最小的最小割，二维费用首先想到费用流，但是很遗憾这题需要求最小割。观察一下代价的性质，最小割边数不超过 n，由此引发出一个清奇的思路，把原来每条边的容量设成 \(c*n+1\)，这样走一条边相当是同时累加了二维费用，跑 dinic 即可。
problem4【优化建图】
考虑把点按 popcount 奇偶性分类，按题中规则连边，点数 \(n2^n\)，考虑优化，每次增广都会减少 \(n*2-1\) 组匹配，有用的只有 \(k*(n*2-1)\) 组，贪心的选取最大的即可。
problem5【集合划分模型】
一种非常重要的最小割模型，考虑一个集合里的作物的共同代价要么不选，要么就得全放到一个集合里，等价于全不能放在另一个集合里，非常符合最小割的定义。建图：每个点向源汇点分别连容量为放入A/B代价的边，建新点连向源点容量全为放入A的代价，连向在此集合中的点，容量为 inf。
