最短路---Dijkstra学习笔记
最短路---Dijkstra
最近蒟蒻的自己重新学习了一遍最短路,也算有些体会,记录下来。
首先引入问题:在一张图中,从某一顶点出发,沿图的边到达定一个顶点所经过的路径中,各边权值和最小的一条路径。
解决该问题的算法有:Dijkstra算法,Bellman-Ford算法,Floyd算法和SPFA算法
Dijkstra算法:
介绍:Dijkstra算法是单源最短路算法的一种,用于求出发节点到所有可达节点的最短路长度。
限制:路径权值必须为非负数 无负权回路 单源最短路
算法思想:Dijkstra算法运用了贪心的思想,通过不断寻找最短距离的点,用以该点为弧尾的点的边更新其他的路径(松弛)。设起点为start,终点为end,start-->end的最短路径只有两种情况。
1、start--->end (从起点到终点直接为最短路径)
2、Start--->v1--->v2...--->end (从起点通过其他的点到达终点的路径)
算法步骤:
把顶点V分成两组:
S:已经求出最短路径的顶点集合
T=V-S:尚未确定最短路径的顶点集合
1、初始时:令S={V0} T={其余顶点} T中的顶点对应的距离值若存在<V0,Vi>,则为该边的权值,若不存在则为INF(正无穷)
2、从T中选取一个距离最小的顶点W,将该点加入集合S中。并用该点对T中顶点的距离进行修改:若加入w作为中间顶点(V0-->W-->Vn),该路径的距离比不加入W的路径更短,则修改此距离值。
3、重复上述步骤,知道S中包含所有顶点,即S=V为止
算法实现过程中需要两个数组
1、dist数组记录源点到每个点的最短路径大小
2、vis数组记录该点是否已经在集合S中(即是否已经找到到该点的最短路径)
算法过程(手动模拟,QAQ丑字不要介意)
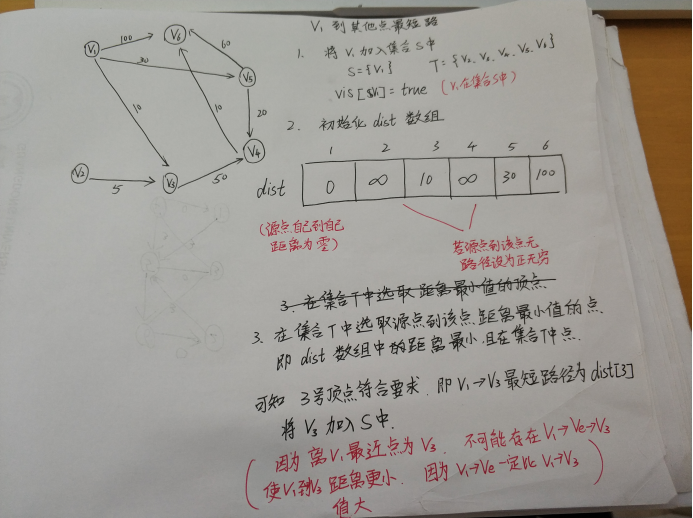


代码实现
这里用一道最短路的模板题来展示该算法的代码。(POJ - 2387 Til the Cows Come Home)
题意:给你n个点,给出a到b的距离,a,b边是可以互想抵达的,求1到n的最短距离。实质:n个顶点m条边的无向图,求1到n的最短路径。
//邻接矩阵存图版本 #include<iostream> #include<cstdio> #include<cstring> using namespace std; const int MAX=1005; const int INF=0x3f3f3f3f; int t,n; //边数 点数 int map[MAX][MAX]; //邻接矩阵存图 int dist[MAX]; //dist数组存源点到各个点的最短路径 bool vis[MAX]; //标记是否找到最小值(是否在集合S中) void Dij(int start) { for(int i=0;i<=n;i++) //初始化 dist全为正无穷,vis全为false { dist[i]=INF; vis[i]=false; } dist[start]=0; //源点到源点的值为0 int min=INF,pos; //寻找dist数组中最小值,并记录其所在的点 for(int i=1;i<=n;i++) { min=INF; for(int j=1;j<=n;j++) //寻找dist中的最小值 { if(!vis[j]&&dist[j]<min) { min=dist[j]; pos=j; } } vis[pos]=true; //将该点加入集合S中 for(int j=1;j<=n;j++) //用该点为弧尾的边进行松弛操作 { if(!vis[j]&&dist[j]>dist[pos]+map[pos][j]) dist[j]=dist[pos]+map[pos][j]; } } } int main() { while(scanf("%d%d",&t,&n)!=EOF) { for(int i=1;i<=n;i++) //初始化 for(int j=1;j<=n;j++) map[i][j]=INF; for(int j=0;j<t;j++) { int a,b,len; scanf("%d%d%d",&a,&b,&len); if(map[a][b]>len) //去除重边(如果先输入的1 2 10则为点1-->2的距离为10,若在输入1 2 100则为 map[a][b]=map[b][a]=len; //点1-->2的距离为100 但是第二次输入会覆盖第一次输入,该更短的边不见,影响结果) } Dij(1); //以1为源点进行Dijkstra printf("%d\n",dist[n]); } return 0; }
//邻接表存图 #include<iostream> #include<cstdio> #include<vector> #include<cstring> using namespace std; const int MAX=1005; const int INF=0x3f3f3f3f; int t,n,a,b,len; int dist[MAX]; bool vis[MAX]; struct point { int to,val; }; vector<point>e[MAX]; void Dij(int start) { for(int i=1;i<=n;i++) //初始化 { dist[i]=INF; vis[i]=false; } dist[start]=0; //源点到源点距离为0 int min,pos; for(int i=1;i<=n;i++) { min=INF; for(int j=1;j<=n;j++) //找dist数组的最小值 { if(!vis[j]&&dist[j]<min) { min=dist[j]; pos=j; } } vis[pos]=true; for(int j=0;j<e[pos].size();j++) //用找到的点为弧尾的边进行松弛 { int to=e[pos][j].to,val=e[pos][j].val; if(!vis[to]&&dist[to]>dist[pos]+val) dist[to]=dist[pos]+val; } } } int main() { while(scanf("%d%d",&t,&n)!=EOF) { point temp; for(int i=0;i<t;i++) { scanf("%d%d%d",&a,&b,&len); //邻接矩阵存图 temp.to=a,temp.val=len; e[b].push_back(temp); temp.to=b;temp.val=len; e[a].push_back(temp); } Dij(1); printf("%d\n",dist[n]); } return 0; }
//链式前向星存图 #include<iostream> #include<cstring> #include<cstdio> using namespace std; const int MAXN=4009; const int MAX=1009; const int INF=0x3f3f3f3f; int head[MAX],cnt=0; int t,n,a,b,len; int dist[MAX]; bool vis[MAX]; struct Edge{ int next,to,val; }Edge[MAXN]; inline void add(int u,int v,int w) { Edge[cnt].to=v; Edge[cnt].val=w; Edge[cnt].next=head[u]; head[u]=cnt++; } void Dij(int start) { for(int i=0;i<=n;i++) { dist[i]=INF; vis[i]=false; } dist[start]=0; int min,pos; for(int i=1;i<=n;i++) { min=INF; for(int j=1;j<=n;j++) { if(!vis[j]&&dist[j]<min) { min=dist[j]; pos=j; } } vis[pos]=true; for(int i=head[pos];i!=-1;i=Edge[i].next) { int to=Edge[i].to; if(!vis[to]&&dist[to]>dist[pos]+Edge[i].val) dist[to]=dist[pos]+Edge[i].val; } } } int main() { while(scanf("%d%d",&t,&n)!=EOF) { memset(head,-1,sizeof(head)); for(int i=0;i<t;i++) { scanf("%d%d%d",&a,&b,&len); add(a,b,len); add(b,a,len); } Dij(1); printf("%d\n",dist[n]); } return 0; }
如有错误和不足之处欢迎指点,谢谢大家~
参考:
http://www.cnblogs.com/hxsyl/p/3270401.html
https://blog.csdn.net/qq_35644234/article/details/60870719
https://blog.csdn.net/u012469987/article/details/51319574#dijkstra





