2019牛客暑期多校训练营（第一场合集）
J-Fraction Comparision
题目大意：
签到题，比较x/a 和 y/b 的大小，其中x，a，y，b的数据范围为
0≤x,y≤1018 1≤a,b≤109
分析：
1、可以看为带分数的形式，先比较整数部分的大小，之后再比较分数部分的大小
2、java大数类直接比较
#include<iostream> using namespace std; long long x,a,y,b; int main() { while(cin>>x>>a>>y>>b) { if(x/a>y/b) //比较整数部分 cout<<">"<<endl; else if(x/a<y/b) cout<<"<"<<endl; else { if(x%a*b>y%b*a) //分数部分 cout<<">"<<endl; else if(x%a*b<y%b*a) cout<<"<"<<endl; else cout<<"="<<endl; } } return 0; }
import java.math.*; import java.util.*; public class Main { public static void main(String[] args) { Scanner input = new Scanner(System.in); while(input.hasNext()) { BigInteger x = input.nextBigInteger(); BigInteger a = input.nextBigInteger(); BigInteger y = input.nextBigInteger(); BigInteger b = input.nextBigInteger(); BigInteger s1 = x.multiply(b); BigInteger s2 = y.multiply(a); int h = s1.compareTo(s2); if(h == 0)System.out.println("="); else if(h == 1)System.out.println(">"); else System.out.println("<"); } } }
A-Equivalent Prefixes
题目大意：
存在两个长度为n的数组，需要你求出一个q使得区间[1,q]中的各个子区间的最小值下标相同
分析：
1、题目需要求的是区间的最大右端点，使得1到该值的两个数组中的任何子区间满足最小值的下标相同
分析可以得出，一个数字只能影响的区间范围是比他大的数的区间(以这个数为最小值，向两边扩展，他能
向左扩展到第一个比该数小的数，向右也如此)
所以两个数组分别加入一个数，这个数字如果该数字能影响到的区间相同，则他们的最小值下标还是相同
因此可以维护两个单调栈，判断每次进栈后栈内元素个数是否相同，来判断是否符合题目要求不相同则停止，
相同则更新答案
#include<iostream> using namespace std; int n; int a[100009],b[100009]; int sta[100009],stb[100009]; int main() { while(cin>>n) { for(int i=1;i<=n;i++)cin>>a[i]; for(int i=1;i<=n;i++)cin>>b[i]; int ans; int topa=0,topb=0; for(int i=1;i<=n;i++) { while(topa&&sta[topa] > a[i]) topa--; sta[++topa]=a[i]; while(topb&&stb[topb] > b[i]) topb--; stb[++topb]=b[i]; if(topa==topb)ans=i; else break; } cout<<ans<<endl; } return 0; }
2、求出的结果p如果符合题意，则pos<p的区间也是符合题意的，p是单调递增的因此可以用二分的不断
判断当前的值是否满足。可以用ST表预处理两个数组，这样经过logn处理后可以O(1)时间找到区间最小值
的下标，判断当前二分区间[1,mid]中是否满足两个数组的最小值下标相同，如果相同，设最小值下标为pos，
继续递归判断[1,pos-1]和[pos+1,r]是否满足要求，递归到最后均满足要求则表示[1,mid]区间符合。不断二分可
求得结果
#include<iostream> #include<cstring> using namespace std; const int MAX=100009; int a[MAX],b[MAX],n; int dpa[MAX][20],dpb[MAX][20]; void ST() { for(int i=1;i<=n;i++) dpa[i][0]=dpb[i][0]=i; for(int j=1;(1<<j)<=n;j++) for(int i=1;i+(1<<j)-1<=n;i++) { int n=a[dpa[i][j-1]],m=a[dpa[i+(1<<(j-1))][j-1]]; dpa[i][j]=n<m?dpa[i][j-1]:dpa[i+(1<<(j-1))][j-1]; } for(int j=1;(1<<j)<=n;j++) for(int i=1;i+(1<<j)-1<=n;i++) { int n=b[dpb[i][j-1]],m=b[dpb[i+(1<<(j-1))][j-1]]; dpb[i][j]=n<m?dpb[i][j-1]:dpb[i+(1<<(j-1))][j-1]; } } int RMQa(int l,int r) { int k=0; while(1<<(k+1)<=r-l+1) k++; int n=a[dpa[l][k]],m=a[dpa[r-(1<<k)+1][k]]; return n<m?dpa[l][k]:dpa[r-(1<<k)+1][k]; } int RMQb(int l,int r) { int k=0; while(1<<(k+1)<=r-l+1) k++; int n=b[dpb[l][k]],m=b[dpb[r-(1<<k)+1][k]]; return n<m?dpb[l][k]:dpb[r-(1<<k)+1][k]; } bool judge(int l,int r) { if(l>=r)return 1; int s1=RMQa(l,r); int s2=RMQb(l,r); if(s1!=s2) return 0; else return judge(l,s1-1)&&judge(s1+1,r); } int main() { while(cin>>n) { int ans; for(int i=1;i<=n;i++)cin>>a[i]; for(int i=1;i<=n;i++)cin>>b[i]; ST(); int l=1,r=n,mid; while(l<=r) { mid=l+r>>1; if(judge(1,mid)) { l=mid+1; ans=mid; } else r=mid-1; } cout<<ans<<endl; } return 0; }
B-Integration
题目大意：
已知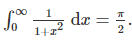
给出a1...an求
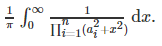结果mod (109+7).
分析：
裂项，找规律，过程如下
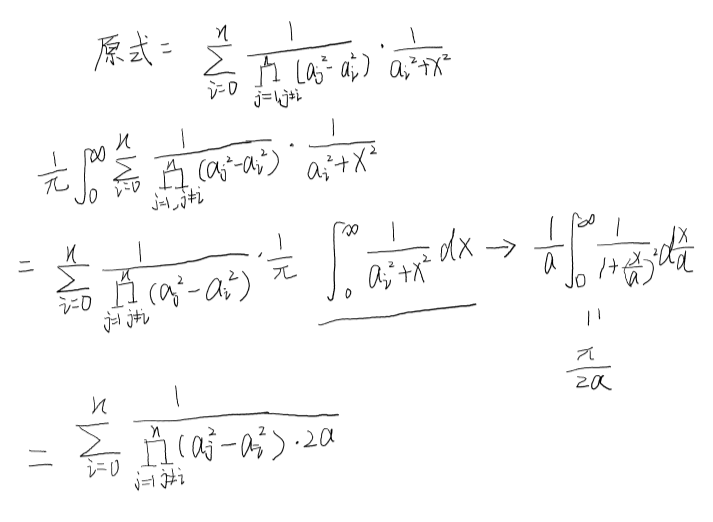
计算上述式子即可
#include<iostream> #include<cmath> using namespace std; typedef long long ll; const int mod=1e9+7; ll pow(ll a, ll b, ll p){ ll ret = 1; while(b){ if(b & 1) ret = (ret * a) % p; a = (a * a) % p; b >>= 1; } return ret; } ll a[1009],cnt; int n; int main() { while(cin>>n) { for(int i=1;i<=n;i++) cin>>a[i]; ll ans=0; for(int i=1;i<=n;i++) { cnt=1; for(int j=1;j<=n;j++) { if(i==j)continue; cnt = cnt * (a[j]*a[j]%mod - a[i]*a[i]%mod)%mod; } ans = (pow(cnt,mod-2,mod) * pow(2*a[i],mod-2,mod) % mod + ans)%mod; } cout<<(ans%mod+mod)%mod<<endl; } return 0; }
E-ABBA
题目大意：
存在长度为2(n+m)的包含A和B的字符串，求解能够分解为n个AB，m个BA的字符串总数
分析:
首先可以发现符合要求的字符串一定能够构成前n个A为与AB匹配的，后m个A是与BA匹配的。因为满足要求的
字符串一定能够构成n个AB与m个BA，只需将前n个A用与匹配AB即可，后面的m个A用于与BA匹配。
这样可以用dp的做法，dp[i][j]表示i个A和j个B满足条件的字符串的种类数
存在两种状态即往字符串中加一个A为dp[i+1][j] 往字符串中加一个B为dp[i][j+1]
对于往字符串中加入一个A我们可以分析：当i<n时我们可以直接加入A，A的位置不受限制，因为A总能与后面
的B匹配得到AB。但当i>n时，我们便不能随便加入A，因为当前已经存在n个A与后面的B构成AB，那么新加入
的A需要和前面的B构成BA才能满足题目要求，因此需要判断前面是否存在足够的B 判定条件为j>i-n 如果满足
才能放入A.
得出
if(i+1<=n) 可以直接放入下一个A else if(i+1>n) //i+1>=n 表示前n个A与AB中B匹配，新加入需与BA中的B匹配 { if(j>i-n) //前面存在足够能与A匹配成为BA的B 可以放入下一个A }
B同理 而放入A和B的递推式也很容易可以得到分别是
dp[i+1][j]=(dp[i][j]+dp[i+1][j])%mod dp[i][j+1]=(dp[i][j]+dp[i][j+1])%mod
代码
#include<iostream> #include<cstring> #include<cstdio> using namespace std; const int MAX=3009; const int mod=1e9+7; int n,m; int dp[MAX][MAX]; int main() { while(~scanf("%d%d",&n,&m)) { for(int i=0;i<=n+m;i++) for(int j=0;j<=n+m;j++) dp[i][j]=0; dp[0][0]=1; for(int i=0;i<=n+m;i++) for(int j=0;j<=n+m;j++) { if(j>i-n)dp[i+1][j]=(dp[i+1][j]+dp[i][j])%mod; if(i>j-m)dp[i][j+1]=(dp[i][j+1]+dp[i][j])%mod; } cout<<dp[n+m][n+m]<<endl; } return 0; }
F-Random Point in Triangle
说实话还没学会QAQ待补坑
#include<iostream> #include<cstring> #include<cmath> #include<cstdio> using namespace std; int main() { long long x1,y1,x2,y2,x3,y3; while(cin>>x1>>y1>>x2>>y2>>x3>>y3) { long long ans=abs(x1*y2+x2*y3+x3*y1-x1*y3-x2*y1-x3*y2); cout<<ans*11<<endl; } return 0; }
H-XOR
题目大意：
给你一个集合S，求集合中所有满足异或和为0的子集大小之和
分析：
求解为子集的大小和，可以转化为求每个元素在集合中出现的次数，算出每个元素的贡献后求和即为答案
题目要求子集要满足异或和的大小和为0，异或的性质c ^ c = 0,因此及判断一个元素能否被其他集合的元素通
过异或的方式表示出来，到这里可以发现用线性基解决此问题。
首先求出n个数字的线性基，设线性基大小为r。
1、在线性基外元素：不在线性基中的n-r个数的任意组合能被线性基所表示（每个数都能被线性基中的元素组合所
表示，每个数的组合异或值也能被元素组合表示），即异或得出结果为0，枚举n-r个数的每个数，都有2(n-r-1)种组
合方式（可以看成该元素一定被选中，剩下n-r-1个元素都有选和不选两种情况），因此线性基外元素贡献为
(n-r) * 2(n-r-1)
2、在线性基内元素：枚举线性基内r个元素每个元素，若剩余n-1个元素能够表示该元素（该元素不能放入剩余n-1
个元素构成的线性基），该元素为线性基外元素，贡献与第一种情况一样，为2(n-r-1) （若该元素能够放入剩余n-1个
元素线性基）则无法用n-1个元素的线性基表示该数，贡献为0
这里求n-1个元素的线性基可以先将第一次处理的n-r个元素的线性基求出，每次往该线性基插入剩余的r-1个元素即可
代码：
#include<iostream> #include<cstring> #include<cstdio> using namespace std; const int MAX=1e5+9; const int mod=1e9+7; typedef long long ll; int n,cnt; ll a[MAX]; //输入的集合 长度为n ll tempa[MAX]; //在线性基中的元素 ll ans; struct LinerBase { int tot; ll b[65]; void init(){ tot=0; memset(b,0,sizeof(b)); } bool insert(ll x){ for(int i=60;i>=0;i--){ if(x&(1ll<<i)){ if(!b[i]){ b[i]=x; tot++; return true; } else x^=b[i]; } } return false; } bool check(ll x){ for(int i=60;i>=0;i--){ if(x&(1ll<<i))x^=b[i]; } return !x; } }Ba,Bb,Bc; //Ba：集合的线性基 长度为r //Bb：不在线性基中的n-r个元素的线性基 //Bc：除去线性基中一个数剩余n-1个数的线性基 ll qpow(ll a,ll n) { ll re=1; while(n) { if(n&1) re=(re*a)%mod; n>>=1; a=(a*a)%mod; } return re%mod; } int main() { while(~scanf("%d",&n)) { Ba.init(),Bb.init(); memset(tempa,0,sizeof(tempa)); ans=0;cnt=0; for(int i=0;i<n;i++) scanf("%lld",&a[i]); for(int i=0;i<n;i++) { if(!Ba.check(a[i])) { Ba.insert(a[i]); tempa[cnt++]=a[i]; } else Bb.insert(a[i]); } if(Ba.tot==n) { printf("0\n"); continue; } ans += (n-Ba.tot) * qpow(2,n-Ba.tot-1) % mod; for(int i=0;i<cnt;i++) { Bc.init(); for(int j=0;j<cnt;j++) if(i!=j)Bc.insert(tempa[j]); for(int j=0;j<=60;j++) if(Bb.b[j]) Bc.insert(Bb.b[j]); if(Bc.check(tempa[i])) ans = (ans + qpow(2,n-Ba.tot-1)) % mod; } printf("%lld\n",ans); } return 0; }
