20180925-6 四则运算试题生成

此作业要求参见：https://edu.cnblogs.com/campus/nenu/2018fall/homework/2148

git地址：https://git.coding.net/gongylx/f4.git

功能一：

四则运算的功能一，最开始分析这个功能时，我和队友选择了用两人较为擅长的python进行编写，通过分析spec，总结出具体框架，要完成的目标是随机生成表达式，在控制台输入答案，后台进行运算与控制台输入的答案进行比较，给出比较的结果，控制表达式数量，用一个变量计算答对题目数目。这里控制台输入的是f4 ,通过控制台终端直接把.py文件转换成.exe程序。所以考虑实现上，决定用python 。利用python 里的random.randint()方法随机生成数字和运算符进行情况判断。这时候的代码如下：

  1 def newint(encoding='utf-8'):
  2     opr = ['+', '-', '*', '/']
  3     fh1 = random.randint(0, 3)
  4     fh2 = random.randint(0, 3)
  5     fh3 = random.randint(0, 3)
  6     n1 = random.randint(1, 20)
  7     n2 = random.randint(1, 20)
  8     n3 = random.randint(1, 20)
  9     n4 = random.randint(1, 20)
 10     rjg = 0
 11     if fh1 == 0:
 12       if fh2 == 0：
 13         if fh3 == 0:
 14           rjg = n1+n2+n3+n4
 15         elif fh3 == 1:
 16           rjg = n1+n2+n3-n4
 17         elif fh3 == 2:
 18           rjg = n1+n2+n3*n4
 19         elif fh3 == 3:
 20           rjg = n1+n2+n3/n4
 21       elif fh2 == 1:
 22         if fh3 == 0:
 23           rjg = n1+n2-n3+n4
 24         elif fh3 == 1:
 25           rjg = n1+n2-n3-n4
 26         elif fh3 == 2:
 27           rjg = n1+n2-n3*n4
 28         elif fh3 == 3:
 29           rjg = n1+n2-n3/n4
 30       elif fh2 == 2:
 31         if fh3 == 0:
 32           rjg = n1+n2*n3+n4
 33         elif fh3 == 1:
 34           rjg = n1+n2*n3-n4
 35         elif fh3 == 2:
 36           rjg = n1+n2*n3*n4
 37         elif fh3 == 3:
 38           rjg = n1+n2*n3/n4
 39       elif fh2 == 3:
 40         if fh3 == 0:
 41           rjg = n1+n2/n3+n4
 42         elif fh3 == 1:
 43           rjg = n1+n2/n3-n4
 44         elif fh3 == 2:
 45           rjg = n1+n2/n3*n4
 46         elif fh3 == 3:
 47           rjg = n1+n2/n3/n4
 48     elif fh1 == 1:
 49       if fh2 == 0:
 50         if fh3 == 0:
 51           rjg = n1-n2+n3+n4
 52         elif fh3 == 1:
 53           rjg = n1-n2+n3-n4
 54         elif fh3 == 2:
 55           rjg = n1-n2+n3*n4
 56         elif fh3 == 3:
 57           rjg = n1-n2+n3/n4
 58       elif fh2 == 1:
 59         if fh3 == 0:
 60           rjg = n1-n2-n3+n4
 61         elif fh3 == 1:
 62           rjg = n1-n2-n3-n4
 63         elif fh3 == 2:
 64           rjg = n1-n2-n3*n4
 65         elif fh3 == 3:
 66           rjg = n1-n2-n3/n4
 67       elif fh2 == 2:
 68         if fh3 == 0:
 69           rjg = n1-n2*n3+n4
 70         elif fh3 == 1:
 71           rjg = n1-n2*n3-n4
 72         elif fh3 == 2:
 73           rjg = n1-n2*n3*n4
 74         elif fh3 == 3:
 75           rjg = n1-n2*n3/n4
 76       elif fh2 == 3:
 77         if fh3 == 0:
 78           rjg = n1-n2/n3+n4
 79         elif fh3 == 1:
 80           rjg = n1-n2/n3-n4
 81         elif fh3 == 2:
 82           rjg = n1-n2/n3*n4
 83         elif fh3 == 3:
 84           rjg = n1-n2/n3/n4
 85     elif fh1 == 2:
 86       if fh2 == 0:
 87         if fh3 == 0:
 88           rjg = n1*n2+n3+n4
 89         elif fh3 == 1:
 90           rjg = n1*n2+n3-n4
 91         elif fh3 == 2:
 92           rjg = n1*n2+n3*n4
 93         elif fh3 == 3:
 94           rjg = n1*n2+n3/n4
 95       elif fh2 == 1:
 96         if fh3 == 0:
 97           rjg = n1*n2-n3+n4
 98         elif fh3 == 1:
 99           rjg = n1*n2-n3-n4
100         elif fh3 == 2:
101           rjg = n1*n2-n3*n4
102         elif fh3 == 3:
103           rjg = n1*n2-n3/n4
104       elif fh2 == 2:
105         if fh3 == 0:
106           rjg = n1*n2*n3+n4
107         elif fh3 == 1:
108           rjg = n1*n2*n3-n4
109         elif fh3 == 2:
110           rjg = n1*n2*n3*n4
111         elif fh3 == 3:
112           rjg = n1*n2*n3/n4
113       elif fh2 == 3:
114         if fh3 == 0:
115           rjg = n1*n2/n3+n4
116         elif fh3 == 1:
117           rjg = n1*n2/n3-n4
118         elif fh3 == 2:
119           rjg = n1*n2/n3*n4
120         elif fh3 == 3:
121           rjg = n1*n2/n3/n4
122     elif fh1 == 3:
123       if fh2 == 0:
124         if fh3 == 0:
125           rjg = n1/n2+n3+n4
126         elif fh3 == 1:
127           rjg = n1/n2+n3-n4
128         elif fh3 == 2:
129           rjg = n1/n2+n3*n4
130         elif fh3 == 3:
131           rjg = n1/n2+n3/n4
132       elif fh2 == 1:
133         if fh3 == 0:
134           rjg = n1/n2-n3+n4
135         elif fh3 == 1:
136           rjg = n1/n2-n3-n4
137         elif fh3 == 2:
138           rjg = n1/n2-n3*n4
139         elif fh3 == 3:
140           rjg = n1/n2-n3/n4
141       elif fh2 == 2:
142         if fh3 == 0:
143           rjg = n1/n2*n3+n4
144         elif fh3 == 1:
145           rjg = n1/n2*n3-n4
146         elif fh3 == 2:
147           rjg = n1/n2*n3*n4
148         elif fh3 == 3:
149           rjg = n1/n2*n3/n4
150       elif fh2 == 3:
151         if fh3 == 0:
152           rjg = n1/n2/n3+n4
153         elif fh3 == 1:
154           rjg = n1/n2/n3-n4
155         elif fh3 == 2:
156           rjg = n1/n2/n3*n4
157         elif fh3 == 3:
158           rjg = n1/n2/n3/n4
159     print(n1, opr[fh1], n2,opr[fh2] ,n3 ,opr[fh3], n4 ,'= ', end='')
160     return rjg

这里实现4个数字和3个运算符的表达式的方法我们俩人都认为比较笨拙，虽然功能实现了，但是代码十分冗余，这里考虑到用栈、逆波兰式去计算，但是又碍于自己的python编程能力还不精进，这时候又考虑到后面的功能2和3，需要加上括号，这时候如果再用列举的方法去实现的话，形式太多，很难实现。这时候选择了更换语言，我们俩商量结果是用老师推荐的 C# 和 VS 环境进行编写，由于本科学习的C#至今没用过，所以我们决定在复习中编码，首先我们俩从网上百度用C#实现四则运算的方法，然后我们俩一人选了一个觉得功能比较全的进行剖析学习，互相讲解，这时候发现了一系列的问题。

对于功能一，首先是用Random方法实现数字和运算符的生成。这里运用switch进行判断识别+-*/，这里遇到的难点是老师spec里讲到的不允许出现除不尽的小数，我们百度了好多，最后选择用度娘的一个方法，我们要避免十进制下的无限小数，只需要让被除数的素因子只有2和5，所以我们将分别判断后三个数为被除数的时候，3种情况下，我们将这3个被除数生成为素因子2和5的幂的形式，这样就保证了表达式结果不会出现无限循环的小数，代码如下:

 1 public class Test
 2     {
 3         public char RandSymbol()//生成运算符
 4         {
 5             Random r = new Random();
 6             int rr = r.Next(4);
 7             switch (rr)
 8             {
 9                 case 0:
10                     return '+';
11                 case 1:
12                     return '-';
13                 case 2:
14                     return '*';
15                 case 3:
16                     return '/';
17                 default:
18                     return '0';
19             }
20         }
21 
22         public int RandNumber()//生成一个0到100的数
23         {
24             Random rn = new Random();
25             return rn.Next(13);
26         }
27         public double ansr = 0;//表达式的结果  
28         public int num1, num2, num3, num4;//生成4个数字进行运算
29         public int n2, m5;//pow(2,n)*pow(5,m)
30         public char op1, op2, op3;//运算符
31         public int BracketPattern;//增加括号
32         public char eq = '=';//等号
33         public char lb = '(';//左括号
34         public char rb = ')';//右括号
35         public string ToEval;//表达式的累加
36         public void GetExp()//获取没有括号的表达式
37         {
38             num1 = RandNumber();
39             System.Threading.Thread.Sleep(15);
40             num2 = RandNumber();
41             System.Threading.Thread.Sleep(15);
42             num3 = RandNumber();
43             System.Threading.Thread.Sleep(15);
44             num4 = RandNumber();
45             System.Threading.Thread.Sleep(15);
46             op1 = RandSymbol();
47             System.Threading.Thread.Sleep(15);
48             op2 = RandSymbol();
49             System.Threading.Thread.Sleep(15);
50             op3 = RandSymbol();
51             if (op1 == '/')//如果我们要避免十进制下的无限小数，只需要让被除数的素因子只有2和5，以下同理。
52             {
53                 Random rd = new Random();
54                 n2 = rd.Next(1, 5);
55                 System.Threading.Thread.Sleep(15);
56                 m5 = rd.Next(1, 3);
57                 num2 = (int)(Math.Pow(2, n2) * Math.Pow(5, m5));
58             }
59             if (op2 == '/')
60             {
61                 Random rd = new Random();
62                 n2 = rd.Next(1, 5);
63                 System.Threading.Thread.Sleep(15);
64                 m5 = rd.Next(1, 3);
65                 num3 = (int)(Math.Pow(2, n2) * Math.Pow(5, m5));
66             }
67             if (op3 == '/')
68             {
69                 Random rd = new Random();
70                 n2 = rd.Next(1, 5);
71                 System.Threading.Thread.Sleep(15);
72                 m5 = rd.Next(1, 3);
73                 num4 = (int)(Math.Pow(2, n2) * Math.Pow(5, m5));
74             }
75             ToEval = num1.ToString() + op1.ToString() + num2.ToString() + op2.ToString() + num3.ToString() + op3.ToString() + num4.ToString();
76             GetAnsr();
77         
78         }

这里为了更好的实现以后的功能，我们采用了后缀表达式和栈的辅助去处理表达式，计算出结果，然后将控制台输入的结果进行比较，得出答案。展示表达式的代码如下：

 1 public void DispExp()//展示表达式
 2         {
 3             string Disp = ToEval + eq;
 4             Console.WriteLine("{0}", Disp);
 5         }
 6         public void DispExpAns(Test t)
 7         {
 8             string Disp = ToEval + eq;
 9             if (Math.Abs((double)Math.Round(t.ansr) - t.ansr) < 1e-7)
10             {
11                 Console.WriteLine("{0,-20}{1,-7}", Disp, (int)t.ansr);
12             }
13             else
14             {
15                 string floatValue = t.ansr.ToString();
16                 floatValue = floatValue.TrimEnd('.', '0');
17                 Console.WriteLine("{0,-20}{1,-7}", Disp, floatValue);
18 
19             }
20         }

计算答案的方式采用调用逆波兰的表达式的方法，去计算逆波兰表达式的值传递给计算答案，代码如下：

public void GetAnsr()//计算答案
        {
            string TE = ToEval;
            Random rd = new Random();
            this.ansr = this.Calucate(TE);//调用计算逆波兰表达式的方法
                                          //   Console.WriteLine("ans is {0}", this.ansr);
        }

计算答案的时候就要考虑到的问题便是利用栈去计算逆波兰表达式，这时候要用到的是运算符的优先级，确保表达式是按照规定优先级进行运算的，代码如下:

static bool IsSize(string s)//是运算符
        {
            string ts = "+-*/%^";
            return ts.IndexOf(s) > -1;
        }

        Dictionary<char, int> priorities = null;//优先级
        const string operators = "+-*/%^";
        public void opinit()//初始化优先级
        {
            priorities = new Dictionary<char, int>();
            priorities.Add('#', -1);
            priorities.Add('+', 0);
            priorities.Add('-', 0);
            priorities.Add('*', 1);
            priorities.Add('/', 1);
            priorities.Add('%', 1);
            priorities.Add('^', 2);
        }

具体的利用转逆波兰的方式去计算答案的代码如下：

double Compute(double leftNum, double rightNum, char op)//计算答案
        {
            switch (op)
            {
                case '+': return leftNum + rightNum;
                case '-': return leftNum - rightNum;
                case '*': return leftNum * rightNum;
                case '/': return leftNum / rightNum;
                case '%': return leftNum % rightNum;
                case '^': return Math.Pow(leftNum, rightNum);
                default: return 0;
            }
        }

        bool IsOperator(char op)
        {
            return operators.IndexOf(op) > -1;
        }

        bool IsLeftAssoc(char op)
        {
            return op == '+' || op == '-' || op == '*' || op == '/' || op == '%';
        }

        Queue<object> PreOrderToPostOrder(string expression)//转逆波兰表达式
        {
            var result = new Queue<object>();
            var operatorStack = new Stack<char>();
            operatorStack.Push('#');
            char top, cur, tempChar;
            string tempNum;
            if (expression[0] == '-')
                expression = '0' + expression;
            for (int i = 0, j; i < expression.Length;)
            {
                cur = expression[i++];
                top = operatorStack.Peek();

                if (cur == '(')
                {
                    operatorStack.Push(cur);
                }
                else
                {
                    if (IsOperator(cur))
                    {
                        while (IsOperator(top) && ((IsLeftAssoc(cur) && priorities[cur] <= priorities[top])) || (!IsLeftAssoc(cur) && priorities[cur] < priorities[top]))
                        {
                            result.Enqueue(operatorStack.Pop());
                            top = operatorStack.Peek();
                        }
                        operatorStack.Push(cur);
                    }
                    else if (cur == ')')
                    {
                        while (operatorStack.Count > 0 && (tempChar = operatorStack.Pop()) != '(')
                        {
                            result.Enqueue(tempChar);
                        }
                    }
                    else
                    {
                        tempNum = "" + cur;
                        j = i;
                        while (j < expression.Length && (expression[j] == '.' || (expression[j] >= '0' && expression[j] <= '9')))
                        {
                            tempNum += expression[j++];
                        }
                        i = j;
                        result.Enqueue(tempNum);
                    }
                }
            }
            while (operatorStack.Count > 0)
            {
                cur = operatorStack.Pop();
                if (cur == '#') continue;
                if (operatorStack.Count > 0)
                {

                    top = operatorStack.Peek();
                }

                result.Enqueue(cur);
            }

            return result;
        }

        public double Calucate(string expression)//计算表达式的值
        {
            try
            {
                var rpn = PreOrderToPostOrder(expression);
                var operandStack = new Stack<double>();
                double left, right;
                object cur;
                while (rpn.Count > 0)
                {
                    cur = rpn.Dequeue();
                    if (cur is char)
                    {
                        right = operandStack.Pop();
                        left = operandStack.Pop();
                        operandStack.Push(Compute(left, right, (char)cur));
                    }
                    else
                    {
                        operandStack.Push(double.Parse(cur.ToString()));
                    }
                }
                return operandStack.Pop();
            }
            catch
            {
                throw new Exception("表达式格式不正确！");
            }
        }
    }

主函数里判断控制台输入的是否有-c ，如果没有-c，则实现的便是功能一，这时候通过判断计算答案和表达式结果的比较，这里利用两数相减结果在小数点后7位内相等则判定正确。具体的主函数代码如下：

static void Main(string[] args)
        {
            int num;//输入表达式中的数字
            int cnt = 0;
            int token = 0;
            var arguments = CommandLineArgumentParser.Parse(args);//命令行参数
            int anslen = 1;//用来作为表达式的结果
            double[] ansrep;//排列存储结果
            ansrep = new double[1000];
            ansrep[0] = -23579;
            if (!arguments.Has("-c"))//如果命令行参数没有-c就输出20个算式
                num = 20;
            else
            {
                num = int.Parse(arguments.Get("-c").Next);//命令行参数中得到要输出的表达式数量
                if (num <= 0)
                {
                    throw
                          new Exception("题目数量必须为 正整数！");
                }
                token = 1;
            }
            if (token == 0)
            {
                for (int i = 0; i < num; i++)
                {
                    Test t = new Test();//new Test
                    t.opinit();
                    t.GetBracketExp();
                    // t.GetExp();
                    //t.NoRepeatedAns(anslen, ansrep);
                    ansrep[(anslen++) - 1] = t.ansr;
                    t.DispExp();//显示表达式
                    Console.Write("?");//控制台显示
                    double ans = double.Parse(Console.ReadLine());
                    // Console.WriteLine("{0},{1}",ans,t.ansr);
                    if (Math.Abs(ans - t.ansr) < 1e-7)//答案正确
                    {
                        Console.WriteLine("答对啦，你真是个天才！");
                        cnt++;
                    }
                    else//答案错误
                    {
                        if (Math.Abs((double)Math.Round(t.ansr) - t.ansr) < 1e-7)
                        {
                            Console.WriteLine("再想想吧，答案似乎是{0}喔！ ", (int)t.ansr);
                        }
                        else//十进制
                        {
                            string floatValue = t.ansr.ToString();
                            floatValue = floatValue.TrimEnd('.', '0');
                            Console.WriteLine("再想想吧，答案似乎是{0}喔！", floatValue);

                        }
                    }
                    
                }
                Console.WriteLine("你一共答对{0}道题，共20道题。", cnt);
            }
            else//实现打印
            {
                for (int i = 0; i < num; i++)
                {
                    Test t = new Test();//new Test
                    t.opinit();
                    t.GetBracketExp();
                    ansrep[(anslen++) - 1] = t.ansr;
                    t.DispExpAns(t);//展示表达式和答案

                }
            }
            
        }

这里功能一的实现在控制台直接输入程序名字，然后自动生成默认的20道题，回答正确得到回复，错误得到回复然后告诉正确答案，最后给出答对题目的数量和题目总数量。功能实现如下图所示：

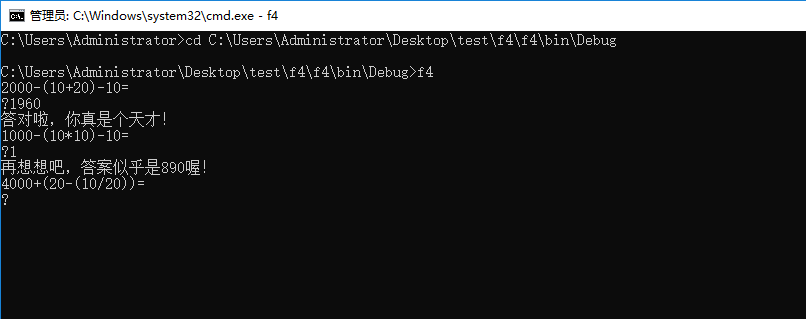
这里默认的20道题结束时，给出总结，如下图：

功能二：

这里功能二的实现是在功能一的基础上实现括号的加入，这里最难的就是当时考虑到括号的加入到底应该如何判断情况，这里我们考虑到的第一种方法是递归的方法，将表达式进行分解，遇到括号的时候先计算括号里面的，然后将结果值存入变量再进行运算。第二种方法便是老师提到的利用栈和逆波兰式进行计算，将所有的表达式入栈，然后利用入栈出栈将相邻最近的两数进行运算，得出总的表达式的值，和计算结果进行比较。

这里最难的地方是括号情况的判断，4个数字和3个运算符，括号位置一共有9种情况，这里同样的要对被除数进行处理，保证答案不会有无限循环的小数，功能实现图与功能一实现图相同，具体代码如下：

 1  public void GetBracketExp()//获取有括号的表达式
 2         {
 3             num1 = RandNumber();
 4             System.Threading.Thread.Sleep(15);
 5             num2 = RandNumber();
 6             System.Threading.Thread.Sleep(15);
 7             num3 = RandNumber();
 8             System.Threading.Thread.Sleep(15);
 9             num4 = RandNumber();
10             System.Threading.Thread.Sleep(15);
11             op1 = RandSymbol();
12             System.Threading.Thread.Sleep(15);
13             op2 = RandSymbol();
14             System.Threading.Thread.Sleep(15);
15             op3 = RandSymbol();
16             Random rdm = new Random();
17             int brkp = rdm.Next(11);//括号存在的方式
18             if (brkp != 0)//brkp为0时不是包含括号的表达式
19             {
20                 Random rd = new Random();
21                 n2 = rd.Next(1, 3);
22                 System.Threading.Thread.Sleep(15);
23                 m5 = rd.Next(1, 2);
24                 num2 = (int)(Math.Pow(2, n2) * Math.Pow(5, m5));
25                 n2 = rd.Next(1, 3);
26                 System.Threading.Thread.Sleep(15);
27                 m5 = rd.Next(1, 2);
28                 num3 = (int)(Math.Pow(2, n2) * Math.Pow(5, m5));
29                 n2 = rd.Next(1, 3);
30                 System.Threading.Thread.Sleep(15);
31                 m5 = rd.Next(1, 2);
32                 num4 = (int)(Math.Pow(2, n2) * Math.Pow(5, m5));
33                 num1 = num2 * num3 * num4;
34             }
35             else
36             {
37                 if (op1 == '/')
38                 {
39                     Random rd = new Random();
40                     n2 = rd.Next(1, 3);
41                     System.Threading.Thread.Sleep(15);
42                     m5 = rd.Next(1, 2);
43                     num2 = (int)(Math.Pow(2, n2) * Math.Pow(5, m5));
44                 }
45                 if (op2 == '/')
46                 {
47                     Random rd = new Random();
48                     n2 = rd.Next(1, 3);
49                     System.Threading.Thread.Sleep(15);
50                     m5 = rd.Next(1, 2);
51                     num3 = (int)(Math.Pow(2, n2) * Math.Pow(5, m5));
52                 }
53                 if (op3 == '/')
54                 {
55                     Random rd = new Random();
56                     n2 = rd.Next(1, 3);
57                     System.Threading.Thread.Sleep(15);
58                     m5 = rd.Next(1, 2);
59                     num4 = (int)(Math.Pow(2, n2) * Math.Pow(5, m5));
60                 }
61             }
62 
63             switch (brkp)
64             {
65                 case 0: ToEval = num1.ToString() + op1.ToString() + num2.ToString() + op2.ToString() + num3.ToString() + op3.ToString() + num4.ToString(); break;
66                 case 1: ToEval = lb.ToString() + num1.ToString() + op1.ToString() + num2.ToString() + rb.ToString() + op2.ToString() + num3.ToString() + op3.ToString() + num4.ToString(); break;
67                 case 2: ToEval = lb.ToString() + num1.ToString() + op1.ToString() + num2.ToString() + op2.ToString() + num3.ToString() + rb.ToString() + op3.ToString() + num4.ToString(); break;
68                 case 3: ToEval = lb.ToString() + lb.ToString() + num1.ToString() + op1.ToString() + num2.ToString() + rb.ToString() + op2.ToString() + num3.ToString() + rb.ToString() + op3.ToString() + num4.ToString(); break;
69                 case 4: ToEval = lb.ToString() + num1.ToString() + op1.ToString() + lb.ToString() + num2.ToString() + op2.ToString() + num3.ToString() + rb.ToString() + rb.ToString() + op3.ToString() + num4.ToString(); break;
70                 case 5: ToEval = num1.ToString() + op1.ToString() + lb.ToString() + num2.ToString() + op2.ToString() + num3.ToString() + rb.ToString() + op3.ToString() + num4.ToString(); break;
71                 case 6: ToEval = num1.ToString() + op1.ToString() + lb.ToString() + lb.ToString() + num2.ToString() + op2.ToString() + num3.ToString() + rb.ToString() + op3.ToString() + num4.ToString() + rb.ToString(); break;
72                 case 7: ToEval = num1.ToString() + op1.ToString() + lb.ToString() + num2.ToString() + op2.ToString() + num3.ToString() + op3.ToString() + num4.ToString() + rb.ToString(); break;
73                 case 8: ToEval = num1.ToString() + op1.ToString() + lb.ToString() + num2.ToString() + op2.ToString() + lb.ToString() + num3.ToString() + op3.ToString() + num4.ToString() + rb.ToString() + rb.ToString(); break;
74                 case 9: ToEval = lb.ToString() + num1.ToString() + op1.ToString() + num2.ToString() + rb.ToString() + op2.ToString() + lb.ToString() + num3.ToString() + op3.ToString() + num4.ToString() + rb.ToString(); break;
75                 default: ToEval = num1.ToString() + op1.ToString() + num2.ToString() + op2.ToString() + num3.ToString() + op3.ToString() + num4.ToString(); break;
76             }
77             GetAnsr();
78         }

功能三：

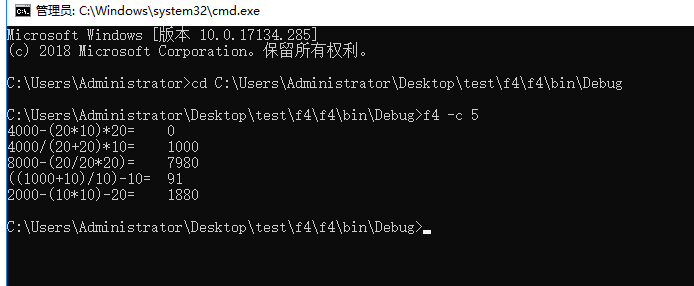
功能三是要在控制台输入-c X，这里的spec要求是将控制台参数作为生成题目数量，这里的难点就是main函数中的情况判断，命令行参数获取类的代码如下：

 public class CommandLineArgument//命令行参数获取类
    {
        List<CommandLineArgument> _arguments;

        int _index;

        string _argumentText;

        public CommandLineArgument Next
        {
            get
            {
                if (_index < _arguments.Count - 1)
                {
                    return _arguments[_index + 1];
                }

                return null;
            }
        }
        public CommandLineArgument Previous
        {
            get
            {
                if (_index > 0)
                {
                    return _arguments[_index - 1];
                }

                return null;
            }
        }
        internal CommandLineArgument(List<CommandLineArgument> args, int index, string argument)
        {
            _arguments = args;
            _index = index;
            _argumentText = argument;
        }

        public CommandLineArgument Take()
        {
            return Next;
        }

        public IEnumerable<CommandLineArgument> Take(int count)
        {
            var list = new List<CommandLineArgument>();
            var parent = this;
            for (int i = 0; i < count; i++)
            {
                var next = parent.Next;
                if (next == null)
                    break;

                list.Add(next);

                parent = next;
            }

            return list;
        }

        public static implicit operator string(CommandLineArgument argument)
        {
            return argument._argumentText;
        }

        public override string ToString()
        {
            return _argumentText;
        }
    }
    public class CommandLineArgumentParser//命令行参数解析器
    {

        List<CommandLineArgument> _arguments;
        public static CommandLineArgumentParser Parse(string[] args)
        {
            return new CommandLineArgumentParser(args);
        }

        public CommandLineArgumentParser(string[] args)
        {
            _arguments = new List<CommandLineArgument>();

            for (int i = 0; i < args.Length; i++)
            {
                _arguments.Add(new CommandLineArgument(_arguments, i, args[i]));
            }

        }

        public CommandLineArgument Get(string argumentName)
        {
            return _arguments.FirstOrDefault(p => p == argumentName);
        }

        public bool Has(string argumentName)
        {
            return _arguments.Count(p => p == argumentName) > 0;
        }
    }
}

功能实现图：

对于结对编程的体会：

结对编程的最大好处就在于能够结合俩个人的算法逻辑方面的思维，设计出更为优秀的算法，提高代码质量。结对编程中，双方的互动目的在于开启思路，避免单独编程时思维容易阻塞的情况。在编程期间，两人的角色切换至少6次，两人轮流，不会太过与疲惫。编程耗时最多的方面就是debug，在我们得出设计思路，并将它们初次转化成代码后，编程之路其实才走了一小段。由于个人的疏忽，输入的错误，以及设计思路的偏差，往往会让我们的程序陷入无止尽的BUG泥潭中，难以挣脱，这会消耗我们大量的时间。而结对编程的好处就在于此，由于身边有个领航员角色的存在，在编写代码时，一旦出现输入错误，就会有人及时的提醒。并且，在设计代码时，有个同伴可以一起讨论，融合两个人不同的见解和观点，我们往往可以得出更加准确且更加高效的设计思路。这一切都为我们在完成代码后的debug过程省去了大量的时间。就我们本次实验一的编程而言，有了领航员的存在，我们在完成代码后，几乎没有花什么时间在debug上，甚至很多阶段性的代码都是一次通过，这大大提高了我们编程的效率，而且我们二人一起讨论出来的编程思路，也使得我们的代码功能更全面，效率更高。

5项在编码、争论、复审等活动中花费时间较长，给你较大收获的事件：

（1）第一个争论点是对于编程语言的选择。我擅长Java，而队友擅长Python。后来由于我对Python处于入门阶段，队友对Java完全不通的状态下，且咨询学长学姐后，发现此程序更适合用Python，所以后来初步选择了Python语言。

（2）花费时间较长的在于后期换了语言重新编码。因为用Python实现功能一，我们使用繁琐的 elif 穷举了四个数字以及三种运算符组合的所有情况，导致功能一就使用了300多行代码。在此基础上无法实现功能二。无可奈何之下换了C#语言。虽然后来听说Python有随机生成数字和符号的方法，但也为时已晚。这种临阵换将的做法耗费了大量的编程时间。在以后的编程中，我一定会意志坚定不会遇到困难就轻易转换语言，太过纠结语言并不是成熟的表现。

（3）第二个争论点是利用转逆波兰的方式去计算答案。看到作业要求时，完全忘记了“逆波兰”和“后缀表达式”都是什么。于是我又找出了本科期间的数据结构教材复习一遍，可还是不能完全理解。后来我想到可以用递归方法实现，但是队友坚持利用堆栈和逆波兰，后来我担心递归不符合作业要求，才算和队友达成一致观点使用逆波兰。

（4）第三个争论点是如何处理答案是无限循环小数的情况（即除不尽的情况），我们开始商量的结果是不让被除数为3，后来想到只是不为3还不行，例如13等其他数字也会有这种情况，这时候我们遇到了困难，达到了所学知识的瓶颈，然后我们通过咨询学长，百度，pull别人的代码分析，最终看到了这个解决方法，将被除数设定为素因子只含2和5的数，这时候避免了bug的出现。

（5）较大收获的事件就是重新借此机会复习了一下C#，自从大二学过C#后，就一直没在用过了。十一假期的时候我找出了本科期间的C#教材温习了一遍，虽然达不到精进但终有一些收获，希望在日后学习中自己能够熟练掌握Java，C#和Python。

工作地点：东北师范大学净月二食堂一楼

posted @ 2018-10-08 15:35 Ljr6899 阅读(190) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Ljr6899

20180925-6 四则运算试题生成

公告