2021.1.5 算法实训

这两天进行了学校安排的算法实训，总的感觉就是对算法的复习和具体项目的练习。

一、什么是算法

1.算法：

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制（百度解释）

2.程序等于算法加数据结构

3.算法的优劣一般使用空间复杂度和时间复杂度来计算

空间复杂度：算法当中使用到的内存空间大小

空间复杂度的计算：一般直接判断使用的数据结构是什么，大小用数学模型来表示，比如使用了一个数组，则为n，使用了二维数组则为n2

时间复杂度：算法运算过程中所花费的时间，时间复杂度一般使用公式来表达，比如O(n2)和O(logn),时间复杂度的数学图像越陡，斜率越高，说明时间复杂度越高。越平缓，则时间复杂度较低。

二、常见的算法有哪些

1.蛮力法

A．蛮力排序算法——使用最直接的遍历，循环等方式解决问题，即正向思维暴力破解

蛮力法的经典体现——冒泡排序，此时可以利用冒泡排序的例子进行算法的讲解

2.迭代

A．斐波拉契的迭代算法——迭代的含义为：当前算式的结果将成为下一次算式的输入，即数据不断的更迭代替，最终得到结果。迭代的难点在于如何停止。

3.递归

斐波拉切的递归算法结合其数学表达式比较好解释该表达式表达的即为当前的结果等于前两次计算结果的和

4.分治法

A．查找算法-二分查找

二分查找法分治法中的经典算法，算法思想：在已排好序的数列中（假设升序）

1. 利于对半分的思想将当前数列分为两个部分

2. 比较目标数字与中位数的大小，如果目标大，则舍弃左半部分，如果目标小则舍弃右半部分，并将剩下的另一部分作为当前数列

3. 重复1,2直到找到目标数字或者找不到返回空。

B．排序算法-归并排序

归并排序算法是排序算法中较难的一种，主要运用了两种算法，分治法和递归。基本思想：归并，即将问题化为最小的单元来解决后再合并，对应在排序算法中就是——一次排序多个较为复杂则将问题化为两个数字排序，即将数列变为多个成对数字比较后合并为一个大的数列。

5.动态规划

A．寻找最佳子序列

算法含义：动态规划和分治法的基本含义相同，不同点在于动态规划中每一个分部都是独立解决某一个问题。比如要解决1 +……+100,1加到100，分步骤解法就是先1+2再加3在加4，每一步都可以独立存在。

6.贪心算法——找到局部最优解

A．局部最优解

算法含义：在某些算法或业务要求中，需要的是根据当前所得到的信息去寻找当前认为最优的解，它不一定是最值点，但是一定是极值点。

三、项目案例讲解

1.贪心法求解最佳分票数

代码

#include <iostream>
using namespace std;

// 一张发票最多只能开 100块

int piao(int a[], int n) {
	//发票数量
	int sum = 0;
	//余数 数组
	int* ys = new int[n];

	for (int i = 0; i < n; i++) {
		sum += a[i] / 100;
		ys[i] = a[i] % 100;
	}

	// 贪心
	for (int i = 0; i < n-1; i++) {
		int t = ys[i] + ys[i + 1];
		if (t > 100) {
			sum++;
			ys[i] = 0;
		}
		else {
			ys[i+1] = t;
		}
	}

	//判断最后一次的余数和
	if (ys[n - 1] > 0)
		sum++;

	return sum;
}

int main() {
	// 报销金额
	const int n = 5;
	int m[n] = {960,105,99,101,806};
	cout << "总发票数为：" << piao(m, n) << endl;

	return 0;
}

2.文本相识度匹配

1.参考资料：

https://www.cnblogs.com/dogecheng/p/11470196.html

https://zhuanlan.zhihu.com/p/33164335

http://www.ruanyifeng.com/blog/2013/03/cosine_similarity.html (很详细)

2.流程思路

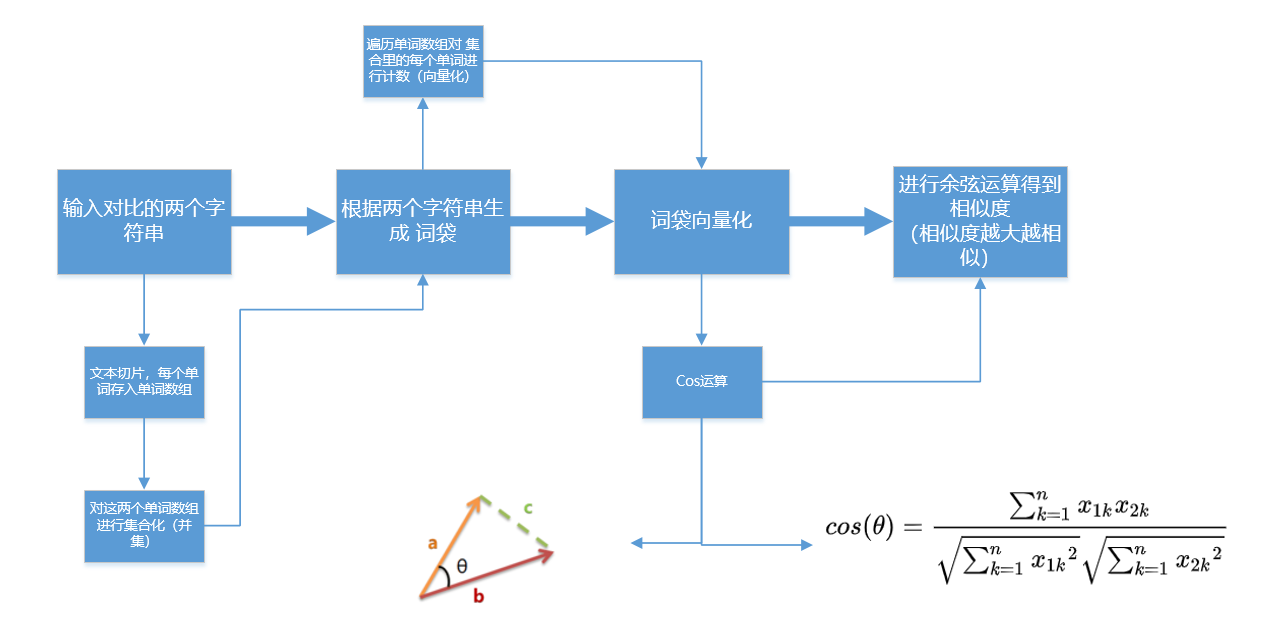
3.非常详细的代码

#include <iostream>
#include <cmath>
#include <string>
using namespace std;

//字符串转单词数组
int toSrtArry(string a, string* StrA) {
    //字符串数组长度 单词数量
    int len = 0;
    //原文本字符串 下标
    int index = 0;
    //临时 单词字符串
    string temp_word;

    //遍历整个文本字符串
    while (a[index] != '\0') {
        //当前字符的 ASCII码
        int int_c1 = (int)a[index];
        //判断当前字符是否为字母
        if ((int_c1 >= 97 && int_c1 <= 122) || (int_c1 >= 65 && int_c1 <= 90)) {
            //将字母添加至临时字符串 做单词
            temp_word.push_back(a[index]);
        }
        //一个单词结束
        else if (temp_word != "") {
            //将单词加入 单词数组
            StrA[len] = temp_word;
            len++;

            //清空单词串
            temp_word = "";
        }
        //下标++
        index++;
    }

    //返回单词数
    return len;
}

//计算词袋
int toModdle(string a, string b, string* moddle) {
    int len = 0;
    //字符串数组 保存 单词
    string* StrA1 = new string[sizeof(string)];
    string* StrA2 = new string[sizeof(string)];
    //调用 toSrtArry 函数 返回单词数
    int len1 = toSrtArry(a, StrA1);
    int len2 = toSrtArry(b, StrA2);

    //遍历单词数组 形成词袋
    int i = 0;
    for (; i < len1; i++) {
        int j = 0;
        for (; j < len; j++) {
            if (moddle[j] == StrA1[i]) {
                break;
            }
        }
        if (j == len)
            moddle[len++] = StrA1[i];
    }

    i = 0;
    for (; i < len2; i++) {
        int j = 0;
        for (; j < len; j++) {
            if (moddle[j] == StrA2[i]) {
                break;
            }
        }
        if (j == len)
            moddle[len++] = StrA2[i];
    }

    return len;
}

//计算余弦相似度
double cosin(int a[], int b[], int n) {

    double divisor1 = 0; //除数
    double divisor2 = 0; //除数
    double dividend = 0; //被除数

    for (int i = 0; i < n; i++) {
        dividend += (a[i] * b[i]);

        divisor1 += (a[i] * a[i]);
        divisor2 += (b[i] * b[i]);
    }

    double d1 = sqrt(divisor1);
    double d2 = sqrt(divisor2);

    return dividend / (d1 * d2);
}

//相似度函数
double xsd(string a, string b, string* moddle, int len) {
    //向量
    int* t1 = new int[len];
    int* t2 = new int[len];
    //单词数组
    string* text1 = new string[sizeof(string)];
    string* text2 = new string[sizeof(string)];
    //单词数
    int len1 = toSrtArry(a, text1);
    int len2 = toSrtArry(b, text2);

    //遍历词袋 计算向量
    for (int i = 0; i < len; i++) {
        //向量初始化
        t1[i] = 0;
        t2[i] = 0;

        //遍历单词数组
        for (int j = 0; j < len1; j++) {
            if (moddle[i] == text1[j])
                t1[i]++;
        }
        for (int k = 0; k < len2; k++) {
            if (moddle[i] == text2[k])
                t2[i]++;
        }
    }

    //输出向量
    //for(int i = 0; i < len; i++) {
    //    cout << t1[i] << ends;
    //}
    //cout << endl;
    //for(int i = 0; i < len; i++) {
    //    cout << t2[i] << ends;
    //} 
    //cout << endl;

    //调用余弦函数，返回相似度
    return cosin(t1, t2, len);
}


int main() {
    //模板字符串数组
    string* moddle = new string[sizeof(string)];

    string text1 = "John likes to watch movies. Mary likes too.";
    string text2 = "John also likes to watch football games.";
    cout << "文本1：" << text1 << endl;
    cout << "文本2：" << text2 << endl;
    cout << "余弦相似度：" << xsd(text1, text2, moddle, toModdle(text1, text2, moddle)) << endl;

    return 0;
}

---