田忌赛马 贪心算法

算法实验课回顾

田忌赛马

问题描述：

你一定听说过田忌赛马的故事吧？如果3匹马变成n匹（n<=100），齐王仍然让他的马按照优到劣的顺序初赛，田忌可以按任意顺序选择他的赛马出赛。赢一局，田忌可以得到200两银子；输一局，田忌就要输掉200两银子。已知道国王和田忌的所有马的奔跑速度，并且所有马的奔跑速度均不相同，现已经对两人的马分别从快到慢排好序。请设计一个算法，帮助田忌赢得最多的银子。

要求：

输入：第一行一个整数n，表示双方各有n匹马；

第二行n个整数分别表示田忌的n匹马的速度；

第三行n个整数分别表示齐王的n匹马的速度。

输出：若通过聪明的你精心安排，如果能赢得比赛（赢的次数大于比赛总次数的一半），那么输出“YES”。 否则输出“NO”。并输出一个整数，代表田忌最多能赢多少两黄金。

1. 如果田忌最快的马比齐王最快的马快，则比之

2. 如果田忌最快的马比齐王最快的马慢，则用田最慢的马跟齐最快的马比

   // 这是贪心的第一步

3. 如果田忌最快的马的速度与齐威王最快的马速度相等

   1. 如果田忌最慢的比齐威王最慢的快，则比之

      // 这是贪心的第二步

   2. 如果田忌最慢的比齐威王最慢的慢，田忌慢VS齐王快

   3. 田忌最慢的与齐威王最慢的相等，田忌慢VS齐王快

代码 C++实现

#include <iostream>
#include <cstdlib>
using namespace std;

// 快排
void Quick(int a[], int begin, int end) {
	if (begin >= end)
		return;

	int t = a[begin];
	int i = begin;
	int j = end;

	while (i < j)
	{
		while (i<j && a[j] < t)
			j--;
		a[i] = a[j];
		while (i < j && a[i] >= t)
			i++;
		a[j] = a[i];
	}
	a[i] = t;
	Quick(a, begin, i - 1);
	Quick(a, i + 1, end);
}

// 田忌赛马算法
int tianRac(int Tian[], int King[], int n) {
	int money = 0; // 田忌赢的钱
	int tianh = 0, tiane = n-1, kingh = 0, kinge = n-1;	// 分别标记田忌马队和齐王马队的最快和最慢的马
	// 共有 n 次比赛，每进行一次，就换下一匹马（田姥爷就位，开始赛马秀）
	for (int i = 0; i < n; i++) {
		// 田忌快马比齐王快马快时，那就和他一较高下（赌怪，必赢）
		if (Tian[tianh] > King[kingh]) {
			money += 200;
			tianh++;	// 下一个
			kingh++;	// 下一个
		}
		// 田忌快马比齐王快马慢时，用最慢的马跟他最快的比（埋伏他一手，这匹马不用抢，他死定了，反手一个超级加倍，闷声发大财）
		else if (Tian[tianh] < King[kingh]) {
			money -= 200;
			tiane--;
			kingh++;
		}
		// 田忌的快马和齐王的快马一样快时（他也一样快？不过不用怕，他的马赢不了我）
		else {
			// 田忌的慢马比齐王的慢马快时（很牛逼这个马）
			if (Tian[tiane] > King[kinge]) {
				money += 200;
				tiane--;
				kinge--;
			}
			// 田忌的慢马比齐王的慢马一样快和慢时，就用慢马和他快马比（如果将这个慢马换成快马我的马将绝杀，可惜换不得）
			else {
				money -= 200;
				tiane--;
				kingh++;
			}
		}
	}
	// 返回田忌赢的钱（飞机~）
	return money;
}

int main() {
	int n;	// 比赛双方马的数量
	cout << "公等马几何" << endl;
	cin >> n;
	int* Tian = new int[n];
	int* King = new int[n];

	cout << "将军 马之疾" << endl;
	for (int i = 0; i < n; i++) {
		cin >> *(Tian + i);
	}
	cout << "王 马之疾" << endl;
	for (int i = 0; i < n; i++){
		cin >> *(King + i);
	}

	// 排序，降序排
	Quick(Tian, 0, n-1);
	Quick(King, 0, n - 1);

	// 调用“就算佛祖来了，田姥爷也难输”算法
	int result = tianRac(Tian, King, n);
	if (result > 0) {
		cout << "将军 胜" << endl;
		cout << "赢 " << result << "金" << endl;
	}
	else if (result == 0)
	{
		cout << "和" << endl;
	}
	else {
		cout << "王 胜" << endl;
		cout << "赢 " << -result << "金" << endl;
	}

	return 0;
}

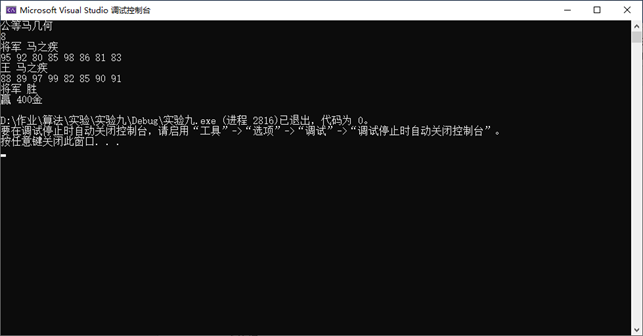
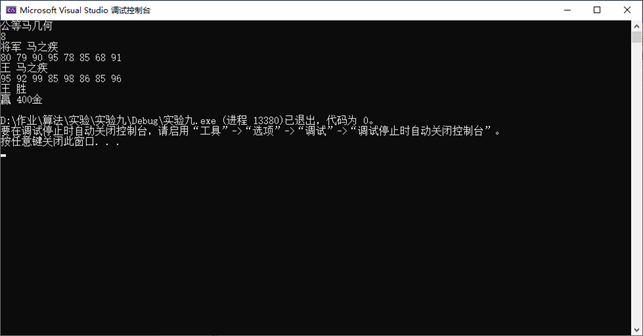
测试数据：

95 92 80 85 98 86 81 83
88 89 97 99 82 85 90 91

80 79 90 95 78 85 68 91
95 92 99 85 98 86 85 96

结果截图：

ps: 这个算法对田姥爷太难输了…