HDU1028 Ignatius and the Princess III

Description

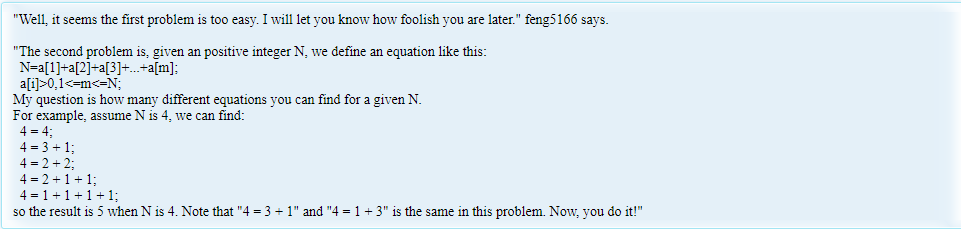
题意：给出 \(n(1\le n\le 120)\)，求出 \(n\) 的整数划分方案数。

Solution

先考虑一个简单的问题：从 \(1\sim n\) 的数字取出若干个数字（每个数字只能取一次），它们的和有多少种方案，每个数又有多少种方案可以得到。

这里给出一个式子：\((1+x)(1+x^2)(1+x^3)\dots(1+x^{n-1})(1+x^n)\)，将这个式子展开后，各项的系数即为组合成该项的指数的方案数。

例如当 \(n=4\) 时，\((1+x)(1+x^2)(1+x^3)(1+x^4)=1+x+x^2+2x^3+2x^4+2x^5+2x^6+2x^7+x^8+x^9+x^{10}\)，那么组成 4 的方案数是 2，组成 8 的方案数是 1 等。

这是什么原理？我们从组合的意义上来理解。

比如说对于第一个括号，\((1+x)\) 中，1 表示不选 1 这个数，\(x\) 表示选 1 这个数，那么就会对最终的答案造成 1 的贡献，表现出来的就是 \(x\) 的指数加一。

那么回到这道题，发现如果在上面那个问题的前提下加上可以重复的条件，那么最后 \(x^n\) 的系数也就是 \(n\) 的整数划分方案数。

为了处理可重复的问题，我们可以对括号稍作修改，式子变为 \((x^{0\times 1}+x^{1\times 1}+x^{2\times 1}+\dots)(x^{0\times 2}+x^{2\times 1}+x^{2\times 2}+\dots)(x^{0\times 3}+x^{1\times 3}+\dots)\dots\)，然后暴力展开求系数即可。

这个方法就是构建了一个生成函数，使得各项系数即为所求答案。

Code

#include<cstdio>
#define N 200
using namespace std;
int n,a[N+5],b[N+5];
int main()
{
    for (int i=0;i<=N;++i)
        a[i]=1,b[i]=0;
    for (int i=2;i<=N;++i)
    {
        for (int j=0;j<=N;++j)
            for (int k=0;k+j<=N;k+=i)
                b[j+k]+=a[j];
        for (int j=0;j<=N;++j)
            a[j]=b[j],b[j]=0;
    }
    while (scanf("%d",&n)!=EOF) printf("%d\n",a[n]);
    return 0;
}