3171. 【GDOI2013模拟4】重心
Description#
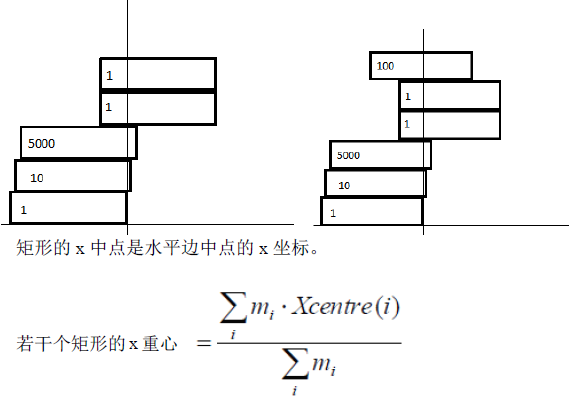
给你N个长2高h的矩形的质量 mi,这 N 个矩形被放置在笛卡尔坐标系中:
- 矩形的四条边平行于坐标轴;
- 每个矩形下面的水平边的y坐标值互不相同,分别是0,h,2h,3h,...,(N-1)h;
- 最下面的矩形的左下角坐标为(-2,0),即右下角在原点处。
一种矩形的摆放方式是稳定的,当且仅当满足:每个矩形上面的所有矩形的 x 重心跟该矩形的 x 中点相距不超过1。上面左图是不稳定的而右图是稳定的。
给你N个矩形的质量,要求在不改变矩形的上下顺序的前提下找到一种稳定的摆放方式,同时输出所有稳定摆放方式中最右边矩形右下角 x 坐标的最大值。
Solution#
先上结论,当我们从上往下做的时候,对于第 i 个块,他对重心的移动量为 mi∑m。
考虑证明,考虑当前为第 i 个块,设 i+1∼n 的块的重心为 0,那么加入第 i 个块后的重心为 ∑nj=iaj×mj∑m=0+ai×mi∑m,而 ai 不是 1 就是 -1,所以加入第 i 个块后对于重心的改变量为 mi∑m。
Code#
#include<cstdio>
#include<algorithm>
#define N 300005
#define db double
using namespace std;
int n,s,a[N];
db ans;
int read()
{
int res=0;char ch=getchar();
while (ch<'0'||ch>'9') ch=getchar();
while (ch>='0'&&ch<='9') res=(res<<1)+(res<<3)+(ch-'0'),ch=getchar();
return res;
}
int main()
{
n=read();
for (int i=1;i<=n;++i)
a[i]=read();
for (int i=n;i>1;--i)
{
s+=a[i];
db x=db(a[i])/db(s);
ans=max(ans,max(ans+x,2-x));
}
printf("%.6lf",ans);
return 0;
}




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 深入理解 Mybatis 分库分表执行原理
· 如何打造一个高并发系统?
· .NET Core GC压缩(compact_phase)底层原理浅谈
· 现代计算机视觉入门之:什么是图片特征编码
· .NET 9 new features-C#13新的锁类型和语义
· Sdcb Chats 技术博客:数据库 ID 选型的曲折之路 - 从 Guid 到自增 ID,再到
· 语音处理 开源项目 EchoSharp
· 《HelloGitHub》第 106 期
· Spring AI + Ollama 实现 deepseek-r1 的API服务和调用
· 使用 Dify + LLM 构建精确任务处理应用