暑假学习笔记
7.9
线段树1(区间加,区间求和)
#include<cstdio>
#include<iostream>
#define re register
#define ll long long
#define maxn 200020
#define ls p<<1
#define rs p<<1|1
#define size (r-l+1)
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
ll ans;
int n,m,opt,x,y,k;
ll Sum[maxn<<2],lazy[maxn<<2],a[maxn];
void push_up(int p)
{
Sum[p]=Sum[ls]+Sum[rs];
}
void push_down(int p,int l,int r)
{
int mid=(l+r)>>1;
lazy[ls]+=lazy[p];
lazy[rs]+=lazy[p];
Sum[ls]+=(mid+1-l)*lazy[p];
Sum[rs]+=(r-mid)*lazy[p];
lazy[p]=0;
}
void build(int l,int r,int p)
{
if(l==r)
{
Sum[p]=a[l];
return;
}
int mid=(l+r)>>1;
build(l,mid,ls);
build(mid+1,r,rs);
push_up(p);
}
void modify(int l,int r,int ql,int qr,int v,int p)
{
if(ql<=l&&r<=qr)
{
Sum[p]+=size*v;
lazy[p]+=v;
return;
}
push_down(p,l,r);
int mid=(l+r)>>1;
if(ql<=mid) modify(l,mid,ql,qr,v,ls);
if(qr>mid) modify(mid+1,r,ql,qr,v,rs);
push_up(p);
}
void query(int l,int r,int ql,int qr,int p)
{
if(ql<=l&&r<=qr)
{
ans+=Sum[p];
return;
}
push_down(p,l,r);
int mid=(l+r)>>1;
if(ql<=mid) query(l,mid,ql,qr,ls);
if(qr>mid) query(mid+1,r,ql,qr,rs);
}
int main()
{
n=read(),m=read();
for(re int i=1;i<=n;++i) a[i]=read();
build(1,n,1);
for(re int i=1;i<=m;++i)
{
opt=read();
if(opt==1)
{
x=read(),y=read(),k=read();
modify(1,n,x,y,k,1);
}
else
{
x=read(),y=read();
ans=0;
query(1,n,x,y,1);
printf("%lld\n",ans);
}
}
return 0;
}
线段树2(区间加,区间乘,区间求和)
理解为什么先下放乘法标记再下放加法标记
#include<cstdio>
#include<iostream>
#define re register
#define maxn 200010
#define ll long long
#define size (r-l+1)
#define ls p<<1
#define rs p<<1|1
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
ll ans;
ll lazy1[maxn<<2],sums[maxn<<2],lazy2[maxn<<2],a[maxn],mod;
int n,m,opt,x,y,k;
void push_up(int p)
{
sums[p]=sums[ls]+sums[rs];
sums[p]%=mod;
}
void push_down(int p,int l,int r)
{
int mid=(l+r)>>1;
lazy2[ls]=(lazy2[p]*lazy2[ls])%mod;
lazy2[rs]=(lazy2[p]*lazy2[rs])%mod;
lazy1[ls]=(lazy2[p]*lazy1[ls])%mod;
lazy1[rs]=(lazy2[p]*lazy1[rs])%mod;
sums[ls]=(sums[ls]*lazy2[p])%mod;
sums[rs]=(sums[rs]*lazy2[p])%mod;
lazy2[p]=1;
lazy1[ls]=(lazy1[p]+lazy1[ls])%mod;
lazy1[rs]=(lazy1[p]+lazy1[rs])%mod;
sums[ls]=(sums[ls]+(mid+1-l)*lazy1[p])%mod;
sums[rs]=(sums[rs]+(r-mid)*lazy1[p])%mod;
lazy1[p]=0;
}
void build(int l,int r,int p)
{
if(l==r)
{
lazy2[p]=1;
sums[p]=a[l];
return;
}
lazy2[p]=1;
int mid=(l+r)>>1;
build(l,mid,ls);
build(mid+1,r,rs);
push_up(p);
}
void modify1(int l,int r,int ql,int qr,int p,int v)
{
if(ql<=l&&r<=qr)
{
sums[p]+=size*v;
sums[p]%=mod;
lazy1[p]+=v;
lazy1[p]%=mod;
return;
}
if((lazy2[p]!=1)||lazy1[p]) push_down(p,l,r);
int mid=(l+r)>>1;
if(ql<=mid) modify1(l,mid,ql,qr,ls,v);
if(qr>mid) modify1(mid+1,r,ql,qr,rs,v);
push_up(p);
}
void modify2(int l,int r,int ql,int qr,int p,int v)
{
if(ql<=l&&r<=qr)
{
sums[p]*=v;
sums[p]%=mod;
lazy1[p]*=v;
lazy1[p]%=mod;
lazy2[p]*=v;
lazy2[p]%=mod;
return;
}
if((lazy2[p]!=1)||lazy2[p]) push_down(p,l,r);
int mid=(l+r)>>1;
if(ql<=mid) modify2(l,mid,ql,qr,ls,v);
if(qr>mid) modify2(mid+1,r,ql,qr,rs,v);
push_up(p);
}
void query(int l,int r,int ql,int qr,int p)
{
if(ql<=l&&r<=qr)
{
ans+=sums[p];
ans%=mod;
return;
}
if((lazy2[p]!=1)||lazy2[p]) push_down(p,l,r);
int mid=(l+r)>>1;
if(ql<=mid) query(l,mid,ql,qr,ls);
if(qr>mid) query(mid+1,r,ql,qr,rs);
}
int main()
{
n=read(),m=read(),mod=read();
for(re int i=1;i<=n;++i) a[i]=read();
build(1,n,1);
for(re int i=1;i<=m;++i)
{
opt=read();
if(opt==1)
{
x=read(),y=read(),k=read();
modify2(1,n,x,y,1,k);
}
else if(opt==2)
{
x=read(),y=read(),k=read();
modify1(1,n,x,y,1,k);
}
else
{
ans=0;
x=read(),y=read();
query(1,n,x,y,1);
printf("%lld\n",ans%mod);
}
}
return 0;
}
归并排序
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<string>
#define re register
#define maxn 50050
#define ll long long
using namespace std;
int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int tmp[maxn],a[maxn],n;
void merge(int l,int mid,int r)
{
int p=0,pl=l,pr=mid+1;
while(pl<=mid&&pr<=r)
{
if(a[pl]<a[pr]) tmp[++p]=a[pl],pl++;
else tmp[++p]=a[pr],pr++;
}
while(pl<=mid) tmp[++p]=a[pl],pl++;
while(pr<=r) tmp[++p]=a[pr],pr++;
for(int i=l;i<=r;++i) a[i]=tmp[i-l+1];
}
void sort(int l,int r)
{
if(l==r) return;
int mid=(l+r)>>1;
sort(l,mid);
sort(mid+1,r);
merge(l,mid,r);
}
int main()
{
n=read();
for(re int i=1;i<=n;++i) a[i]=read();
sort(1,n);
for(re int i=1;i<=n;++i) printf("%d ",a[i]);
return 0;
}
7.10
快速排序\(quicksort\)
注意若以最左边为基准,则要先从右往左扫,保证换到最左边小于等于基准值
#include<cstdio>
#include<iostream>
#include<algorithm>
#define re register
#define maxn 200010
using namespace std;
int n,a[maxn];
void quicksort(int l,int r)
{
if(l>=r) return;
int i=l,j=r,base=a[l];
while(i<j)
{
while(a[j]>=base&&i<j) --j;
while(a[i]<=base&&i<j) ++i;
swap(a[i],a[j]);
}
swap(a[l],a[i]);
quicksort(l,i-1);
quicksort(i+1,r);
}
int main()
{
scanf("%d",&n);
for(re int i=1;i<=n;++i) scanf("%d",a+i);
quicksort(1,n);
for(re int i=1;i<=n;++i) printf("%d ",*(a+i));
return 0;
}
应用:求第\(k\)小数 https://www.luogu.com.cn/problem/P1923#submit
堆排序(小根堆)
#include<cstdio>
#include<iostream>
#include<algorithm>
#define re register
#define maxn 200010
using namespace std;
int n,a[maxn],t[maxn<<1],len;
void siftdown(int c)
{
int nxt=c;
if(2*c<=len&&t[2*c]<t[nxt]) nxt=2*c;
if(2*c+1<=len&&t[2*c+1]<t[nxt]) nxt=2*c+1;
if(nxt==c) return;
swap(t[c],t[nxt]);
siftdown(nxt);
}
void del()
{
t[1]=t[len];
len--;
siftdown(1);
}
int main()
{
scanf("%d",&n);
for(re int i=1;i<=n;++i) scanf("%d",t+i);
len=n;
for(re int i=n/2;i>=1;--i) siftdown(i);
for(re int i=1;i<=n;++i)
{
a[i]=t[1];
del();
}
for(re int i=1;i<=n;++i) printf("%d ",a[i]);
return 0;
}
7.11
倍增求\(LCA\)
注意细节处理:如每次循环的边界,以0为初始节点,lg数组的建立...
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#define re register
#define ll long long
#define maxn 500100
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,m,s;
struct Edge{
int v,nxt;
}e[maxn<<2];
int f[maxn][25],x,y,num,cnt;
int head[maxn],dep[maxn],lg[maxn];
inline void add(int u,int v)
{
e[++cnt].v=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void dfs(int u,int fa)
{
dep[u]=dep[fa]+1;
f[u][0]=fa;
for(int i=1;(1<<i)<=dep[u];++i)
f[u][i]=f[f[u][i-1]][i-1];
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].v;
if(v==fa) continue;
dfs(v,u);
}
}
void pre()
{
int tmp=1;
while(tmp<=n)
{
lg[tmp]=num;
num++;
tmp*=2;
}
for(re int i=1;i<=n;++i)
{
if(lg[i]) continue;
lg[i]=lg[i-1];
}
}
int lca(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=lg[dep[x]-dep[y]];i>=0;--i)
{
if(dep[f[x][i]]<dep[y]) continue;
x=f[x][i];
}
if(x==y) return x;
for(int i=lg[dep[x]-1];i>=0;--i)
{
if(f[x][i]==f[y][i]) continue;
x=f[x][i],y=f[y][i];
}
return f[x][0];
}
int main()
{
n=read(),m=read(),s=read();
for(re int i=1;i<n;++i)
{
x=read(),y=read();
add(x,y);
add(y,x);
}
pre();
dfs(s,0);
for(re int i=1;i<=m;++i)
{
x=read(),y=read();
printf("%d\n",lca(x,y));
}
return 0;
}
7.12
\(Dijkstra\)堆优化\(O(nlogn)\)
#include<cstdio>
#include<queue>
#include<iostream>
#define re register
#define maxn 200010
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct Edge{
int v,w,nxt;
}e[maxn];
int n,m,s;
int a,b,c,ev;
int cnt,head[maxn],vis[maxn],dis[maxn];
inline void add(int u,int v,int w)
{
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
struct node{
int u,d;
bool operator <(const node&rhs)const{
return rhs.d<d;
}
};
void dijkstra()
{
priority_queue<node> q;
dis[s]=0;
q.push((node){s,0});
while(!q.empty())
{
node f=q.top();
q.pop();
int now=f.u,dd=f.d;
if(vis[now]) continue;
vis[now]=1;
for(int i=head[now];i;i=e[i].nxt)
{
ev=e[i].v;
if(dis[ev]>dis[now]+e[i].w)
{
dis[ev]=dis[now]+e[i].w;
if(!vis[ev])
{
q.push((node){ev,dis[ev]});
}
}
}
}
}
int main()
{
n=read(),m=read(),s=read();
for(re int i=1;i<=n;++i) dis[i]=0x7fffffff;
for(re int i=1;i<=m;++i)
{
a=read(),b=read(),c=read();
add(a,b,c);
}
dijkstra();
for(re int i=1;i<=n;++i)
printf("%d ",dis[i]);
return 0;
}
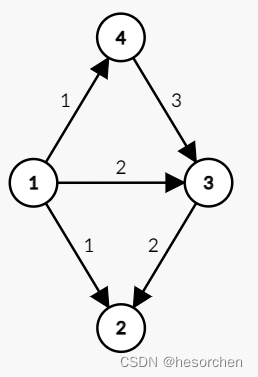
\(dijkstra\)不能用来求有负权边的最短路,不能用来求正权图的最短路(基于贪心思想,每个点只会更新一次,且保证用子结构最优,即最先更新的一定是最短点更新,最长路就存在贪心反例了)或负权图的最长路。
7.13
\(SPFA\)
\(dijkstra\)是贪心,每次用最近的点更新,而\(SPFA\)是不断用队首的点松弛,一个点可以入队多次
\(SPFA\)可以处理负权边,可以判断负环
注意\(memset\)的使用,不能直接赋\(0x7fffffff\)
\(SPFA\)是基于\(BFS\)的
#include<cstdio>
#include<iostream>
#include<queue>
#include<cstring>
#define maxn 500010
#define re register
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct Edge{
int v,w,nxt;
}e[maxn];
int cnt,head[maxn],n,m,a,b,c,s;
int dis[maxn],vis[maxn];
inline void add(int u,int v,int w)
{
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int eu,ev;
void spfa()
{
dis[s]=0;
queue<int> q;
q.push(s);
vis[s]=1;
while(!q.empty())
{
eu=q.front();
q.pop();
vis[eu]=0;
for(int i=head[eu];i;i=e[i].nxt)
{
ev=e[i].v;
if(dis[ev]>dis[eu]+e[i].w)
{
dis[ev]=dis[eu]+e[i].w;
/*判负环
cnt[ev]=cnt[eu]+1;
if(cnt[ev]>n) {printf("false");return;}*/
if(!vis[ev])
{
vis[ev]=1;
q.push(ev);
}
}
}
}
}
int main()
{
n=read(),m=read(),s=read();
for(re int i=1;i<=m;++i)
{
a=read(),b=read(),c=read();
add(a,b,c);
}
for(int i = 1; i <= n; ++i)dis[i] = 0x7fffffff;
dis[0]=0;
spfa();
for(re int i=1;i<=n;++i)
printf("%d ",dis[i]);
return 0;
}

$SPFA双端队列优化:把小的从前面入队,大的从后面入队,每次从前面出
7.14
STL堆
#include <queue>
priority_queue<int> pq1 // 大根堆
priority_queue<int, vector<int>, greater<int>> pq2 // 小根堆
自定义堆的两种写法
struct node{
int u,d;
bool operator <(const node&rhs)const {
return rhs.d<d;
}
};
struct cmp{
bool operator ()(int &x,int &y)
{
return dis[x]>dis[y];//注意这>是定义了小根堆
}
};
priority_queue<node> q;
priority_queue<int,vector<int>,cmp> q;
堆优化\(SPFA\)
#include<cstdio>
#include<iostream>
#include<queue>
#include<cstring>
#define maxn 500010
#define INF 88
#define re register
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct Edge{
int v,w,nxt;
}e[maxn];
int cnt,head[maxn],n,m,a,b,c,s;
int dis[maxn],vis[maxn];
inline void add(int u,int v,int w)
{
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int eu,ev;
struct cmp{
bool operator ()(int &x,int &y)
{
return dis[x]>dis[y];
}
};
void spfa()
{
dis[s]=0;
priority_queue<int,vector<int>,cmp> q;
q.push(s);
vis[s]=1;
while(!q.empty())
{
eu=q.top();
q.pop();
vis[eu]=0;
for(int i=head[eu];i;i=e[i].nxt)
{
ev=e[i].v;
if(dis[ev]>dis[eu]+e[i].w)
{
dis[ev]=dis[eu]+e[i].w;
if(!vis[ev])
{
vis[ev]=1;
q.push(ev);
}
}
}
}
}
int main()
{
n=read(),m=read(),s=read();
for(re int i=1;i<=m;++i)
{
a=read(),b=read(),c=read();
add(a,b,c);
}
memset(dis,127,sizeof(dis));
dis[0]=0;
spfa();
for(re int i=1;i<=n;++i)
printf("%d ",dis[i]);
return 0;
}
7.17
割点
在\(dfs\)树中讨论
\(LOW[x]\)的含义是不通过父节点能到达的最早节点
由割点的要求,当找到早节点时,应该用\(DFN[ev]\)而不是\(LOW[ev]\)更新
#include<cstdio>
#include<iostream>
#define re register
#define maxn 200010
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct Edge{
int v,nxt;
}e[maxn<<2];
int n,m,x,y,flag[maxn],ans;
int cnt,head[maxn],DFN[maxn],LOW[maxn],Index;
inline void add(int u,int v)
{
e[++cnt].v=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void dfs(int x,int fa)
{
int child=0;
DFN[x]=LOW[x]=++Index;
for(int i=head[x];i;i=e[i].nxt)
{
int ev=e[i].v;
if(!DFN[ev])
{
dfs(ev,fa);
LOW[x]=min(LOW[x],LOW[ev]);
if(LOW[ev]>=DFN[x]&&(x!=fa)) flag[x]=1;
if(x==fa) child++;
}
LOW[x]=min(LOW[x],DFN[ev]);
}
if(x==fa&&child>=2) flag[x]=1;
}
int main()
{
n=read(),m=read();
for(re int i=1;i<=m;++i)
{
x=read(),y=read();
add(x,y);
add(y,x);
}
for(re int i=1;i<=n;++i)
if(!DFN[i]) dfs(i,i);
for(re int i=1;i<=n;++i)
if(flag[i]) ans++;
printf("%d\n",ans);
for(re int i=1;i<=n;++i)
if(flag[i]) printf("%d ",i);
return 0;
}
7.19
\(DAG\)(有向无环图上)\(toposort\)
栈、队列均可
void toposort()
{
stack<int> s;
for(re int i=1;i<=n;++i) if(!du[i]) s.push(i);
while(!s.empty())
{
int u=s.top();
ans[++cnt]=now;
s.pop();
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].v;
if(--du[v]==0) s.push(v);
}
}
if(cnt!=n) printf("Ilegal!");
else for(re int i=1;i<=n;++i) printf("%d ",ans[i]);
}
也可用\(dfs\)回溯时记录形成拓扑序
\(tarjan\)缩点
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define re register
using namespace std;
const int maxn =1e5+1e4,maxm =1e5+1e4;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int Index,vis[maxn],num[maxn],low[maxn];
int tot,color[maxn],Sum[maxn],f[maxn];
int cnt,head[maxn],nxt[maxm],to[maxm];
int stack[maxn],top;
int n,m,val[maxn],x[maxn],y[maxn],ans;
inline void add(int u,int v)
{
to[++cnt]=v;
nxt[cnt]=head[u];
head[u]=cnt;
}
void tarjan(int x)
{
low[x]=num[x]=++Index;
stack[++top]=x;
vis[x]=1;
for(int i=head[x];i;i=nxt[i])
{
int v=to[i];
if(!num[v])
{
tarjan(v);
low[x]=min(low[x],low[v]);
}
else if(vis[v])
{
low[x]=min(low[x],low[v]);
}
}
if(low[x]==num[x])
{
tot++;
while(stack[top+1]!=x)
{
color[stack[top]]=tot;
Sum[tot]+=val[stack[top]];
vis[stack[top--]]=0;
}
}
}
void search(int x)//记忆化搜索找最长权值路径,可用toposort+dp代替
{
if(f[x]) return;
f[x]=Sum[x];
int maxsum=0;
for(int i=head[x];i;i=nxt[i])
{
int v=to[i];
if(!f[v]) search(v);
maxsum=max(maxsum,f[v]);
}
f[x]+=maxsum;
}
int main()
{
n=read(),m=read();
for(re int i=1;i<=n;++i) val[i]=read();
for(re int i=1;i<=m;++i)
{
x[i]=read(),y[i]=read();
add(x[i],y[i]);
}
for(re int i=1;i<=n;++i) if(!num[i]) tarjan(i);
memset(head,0,sizeof(head));
memset(nxt,0,sizeof(nxt));
memset(to,0,sizeof(to));
cnt=0;
for(re int i=1;i<=m;++i)
{
if(color[x[i]]!=color[y[i]])
add(color[x[i]],color[y[i]]);
}
for(re int i=1;i<=tot;++i)
{
if(!f[i])
{
search(i);
ans=max(ans,f[i]);
}
}
printf("%d",ans);
return 0;
}
并查集(按秩合并、路径压缩)
int find(int x)
{
return fa[x]==x?x:(fa[x]=find(fa[x])); //路径压缩数据大时用递归可能会爆栈,可以写while
}
void merge(int i,int j)
{
int x=find(i),y=find(j);
if(x==y) return;
if(rank[x]<rank[y])
fa[x]=y;
else
fa[y]=x;
if(rank[x]==rank[y]) rank[x]++;
}
7.20
树链剖分
利用重链和子树上节点编号连续,用线段树维护
注意两个\(dfs\)分别的作用
注意链的两个端点是怎么交替跳的
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define re register
#define maxn 200010
#define ll long long
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
ll mod,sums[maxn<<2],lazy[maxn],res,ans;
int son[maxn],maxson,id[maxn],top[maxn];
int w[maxn],wt[maxn],dep[maxn],fa[maxn],siz[maxn];
int cnt,head[maxn],n,m,root,opt,x,y,z,num;
struct Edge{
int v,nxt;
}e[maxn<<2];
inline void add(int u,int v)
{
e[++cnt].v=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
//------------------线段树-------------------
#define ls p<<1
#define rs p<<1|1
#define size (r-l+1)
void push_down(int p,int l,int r)
{
lazy[p]%=mod;
lazy[ls]=(lazy[ls]+lazy[p])%mod;
lazy[rs]=(lazy[rs]+lazy[p])%mod;
int mid=(l+r)>>1;
sums[ls]=(sums[ls]+lazy[p]*(mid+1-l))%mod;
sums[rs]=(sums[rs]+lazy[p]*(r-mid))%mod;
lazy[p]=0;
}
void push_up(int p){sums[p]=(sums[ls]+sums[rs])%mod;}
void build(int l,int r,int p)
{
if(l==r)
{
sums[p]=wt[l];
return;
}
int mid=(l+r)>>1;
build(l,mid,ls);
build(mid+1,r,rs);
push_up(p);
}
void update(int p,int l,int r,int ql,int qr,int k)
{
if(ql<=l&&r<=qr)
{
sums[p]=(sums[p]+k*size)%mod;
lazy[p]=(lazy[p]+k)%mod;
return;
}
push_down(p,l,r);
int mid=(l+r)>>1;
if(ql<=mid) update(ls,l,mid,ql,qr,k);
if(qr>mid) update(rs,mid+1,r,ql,qr,k);
push_up(p);
}
void query(int p,int l,int r,int ql,int qr)
{
if(ql<=l&&r<=qr)
{
res=(sums[p]+res)%mod;
return;
}
push_down(p,l,r);
int mid=(l+r)>>1;
if(ql<=mid) query(ls,l,mid,ql,qr);
if(qr>mid) query(rs,mid+1,r,ql,qr);
}
//---------------线段树--------------
void dfs1(int u,int fat,int deep)
{
dep[u]=deep;
fa[u]=fat;
siz[u]=1;
maxson=-1;
for(int i=head[u];i;i=e[i].nxt)
{
int ev=e[i].v;
if(ev==fat) continue;
dfs1(ev,u,deep+1);
siz[u]+=siz[ev];
if(siz[ev]>maxson) maxson=siz[ev],son[u]=ev;
}
}
void dfs2(int u,int topf)
{
id[u]=++num;
wt[num]=w[u];
top[u]=topf;
if(!son[u]) return;
dfs2(son[u],topf);
for(int i=head[u];i;i=e[i].nxt)
{
int ev=e[i].v;
if(ev==fa[u]) continue;
if(son[u]==ev) continue;
dfs2(ev,ev);
}
}
void addRange(int x,int y,int z)
{
z%=mod;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);//这样交换着跳,保证不会窜过了
update(1,1,n,id[top[x]],id[x],z);
x=fa[top[x]];//到另一条链上
}
if(dep[y]>dep[x]) swap(x,y);
update(1,1,n,id[y],id[x],z);
}
void addSon(int x,int z)
{
z%=mod;
update(1,1,n,id[x],id[x]+siz[x]-1,z);
}
void qSon(int x)
{
res=0;
query(1,1,n,id[x],id[x]+siz[x]-1);
ans=(ans+res)%mod;
}
void qRange(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
res=0;
query(1,1,n,id[top[x]],id[x]);
ans=(ans+res)%mod;
x=fa[top[x]];
}
if(dep[x]<dep[y]) swap(x,y);
res=0;
query(1,1,n,id[y],id[x]);
ans=(ans+res)%mod;
}
int main()
{
n=read(),m=read(),root=read(),mod=read();
for(re int i=1;i<=n;++i) w[i]=read();
for(re int i=1;i<n;++i)
{
x=read(),y=read();
add(x,y);
add(y,x);
}
dfs1(root,0,1);
dfs2(root,root);
build(1,n,1);
for(re int i=1;i<=m;++i)
{
opt=read();
if(opt==1)
{
x=read(),y=read(),z=read();
addRange(x,y,z);
}
else if(opt==2)
{
x=read(),y=read();
//printf("x:%d y:%d\n",x,y);
ans=0;
qRange(x,y);
printf("%lld\n",ans);
}
else if(opt==3)
{
x=read(),z=read();
addSon(x,z);
}
else
{
x=read();
ans=0;
qSon(x);
printf("%lld\n",ans);
}
}
return 0;
}
7.21
树状数组 单点修改,区间查询
#include<cstdio>
#include<iostream>
#define re register
#define lowbit(x) x&(-x)
#define maxn 500010
using namespace std;
int n,m,x,opt,y,k,ans;
int s[maxn<<1];
inline void add(int x,int k)
{
while(x<=n)
{
s[x]+=k;
x+=lowbit(x);
}
}
inline int query(int x)
{
int ans=0;
while(x>0)
{
ans+=s[x];
x-=lowbit(x);
}
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(re int i=1;i<=n;++i)
{
scanf("%d",&x);
add(i,x);
}
for(re int i=1;i<=m;++i)
{
scanf("%d%d%d",&opt,&x,&y);
if(opt==1) add(x,y);
else
{
printf("%d\n",query(y)-query(x-1));
}
}
return 0;
}
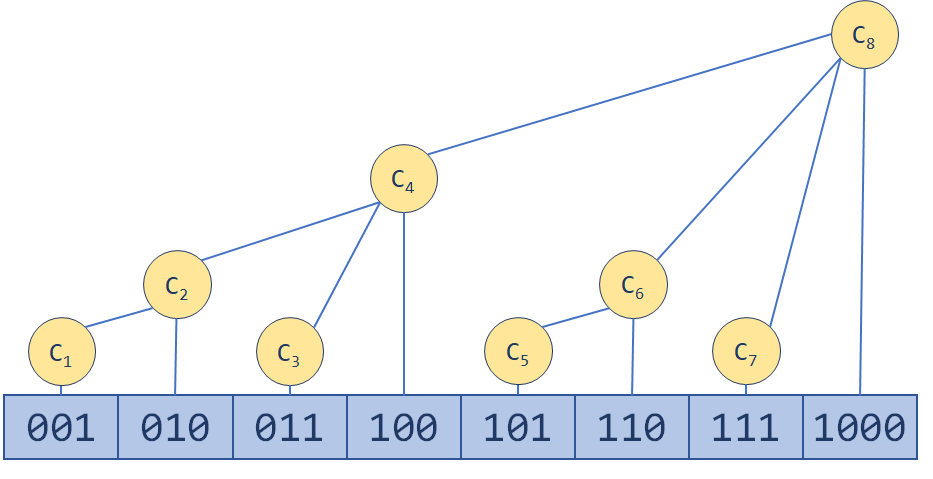
\(s[x]\)表示\((x-lowbit(x),x]\)的区间和
求和时求的是\([1,x]\)的和,从\(x\)不断减\(lowbit(x)\)跳到下一个区间
单点修改时需要对所有影响的区间更新,每次\(+lowbit(x)\)即可
7.22
最小生成树\(prim\)--->无向图中最小生成树(最小无环图)
复杂度\(O(n^2)\)
基于\(dijkstra\)的贪心,每次循环要做的事是:1.遍历,找到一个距离已有节点集合最近的点2.用这个点更新他的未到达的相邻节点
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define INF 0x3f3f3f3f
#define re register
#define maxn 50010
#define maxm 200010
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f ;
}
int n,m,ans,minn,now,vis[maxn],head[maxn],x,y,z,cnt,tot;
int dis[maxn],ev;
bool flag;
struct Edge{
int v,w,nxt;
}e[maxm<<2];
inline void add(int u,int v,int w)
{
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
inline int prim()
{
memset(dis,INF,sizeof(dis));
dis[1]=0;
for(re int i=head[1];i;i=e[i].nxt)
{
ev=e[i].v;
dis[ev]=min(dis[ev],e[i].w);
}
now=1;
while(++tot<n)
{
minn=INF;
flag=false;
vis[now]=1;
for(re int i=1;i<=n;++i)
{
if(!vis[i]&&minn>dis[i])
{
minn=dis[i];
now=i;
flag=true;//判断是否存在最小生成树(是否连通)
}
}
if(!flag)
{
printf("orz\n");
exit(0);
}
ans+=minn;
for(re int i=head[now];i;i=e[i].nxt)
{
ev=e[i].v;
if(dis[ev]>e[i].w&&!vis[ev])
{
dis[ev]=e[i].w;
}
}
}
return ans;
}
int main()
{
n=read(),m=read();
for(re int i=1;i<=m;++i)
{
x=read(),y=read(),z=read();
add(x,y,z);
add(y,x,z);
}
printf("%d\n",prim());
return 0;
}
7.25
树状数组区间修改、区间查询
观察到要求的前缀和
只需维护\(\sum\limits_{i=1}^pd[i]\)和\(\sum\limits_{i=1}^pd[i]*i\)即可
#include<cstdio>
#include<iostream>
#define re register
#define maxn 200010
#define ll long long
#define lowbit(x) x&(-x)
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
ll sums1[maxn<<2],sums2[maxn<<2];
int n,m,opt,x,y,k,a[maxn];
inline void add(int x,int k)
{
int pos=x;
while(x<=n)
{
sums1[x]+=k;
sums2[x]+=pos*k;
x+=lowbit(x);
}
}
inline ll query(int x)
{
int pos=x;
ll ans=0;
while(x>0)
{
ans+=(pos+1)*sums1[x]-sums2[x];
x-=lowbit(x);
}
return ans;
}
int main()
{
n=read(),m=read();
for(re int i=1;i<=n;++i)
{
a[i]=read();
add(i,a[i]-a[i-1]);
}
for(re int i=1;i<=m;++i)
{
opt=read();
if(opt==1)
{
x=read(),y=read(),k=read();
add(x,k),add(y+1,-k);
}
else
{
x=read(),y=read();
printf("%lld\n",query(y)-query(x-1));
}
}
return 0;
}
7.26
二维树状数组
1.单点修改,区间查询
将一维的扩展为二维即可,求前缀和需要容斥
2.区间修改,单点查询
求差分数组
注意到有\(sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]\)
故有\(a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+d[i][j]\)
由此得到差分数组\(d\)分布规律
3.区间查询,区间修改
维护四个数组

#include<cstdio>
#include<iostream>
#include<cstring>
#define ll long long
#define maxn 2110
#define lowbit(x) x&(-x)
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int sums1[maxn][maxn],sums2[maxn][maxn],sums3[maxn][maxn],sums4[maxn][maxn];
int n,m,a,b,c,d,k;
char f[3];
inline void add(int x,int y,int k)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
{
sums1[i][j]+=k;
sums2[i][j]+=k*y;
sums3[i][j]+=k*x;//注意加的是定值,不要写成k*i
sums4[i][j]+=k*x*y;
}
}
inline ll query(int x,int y)
{
ll ans=0;
for(int i=x;i>0;i-=lowbit(i))
for(int j=y;j>0;j-=lowbit(j))
{
ans+=(x+1)*(y+1)*sums1[i][j]-(x+1)*sums2[i][j]-(y+1)*sums3[i][j]+sums4[i][j];
}//不要把x+1写成i+1
return ans;
}
int main()
{
scanf("X %d %d",&n,&m);
while(~scanf("%s",&f))
{
a=read(),b=read(),c=read(),d=read();
if(f[0]=='L')
{
k=read();
add(a,b,k),add(a,d+1,-k),add(c+1,b,-k),add(c+1,d+1,k);
}
else
{
printf("%lld\n",query(c,d)-query(c,b-1)-query(a-1,d)+query(a-1,b-1));
}
}
return 0;
}
7.27
权值线段树与离散化
权值线段树:若\(p\)节点表示的区间是\(l-r\),则代表值为\(l-r\)的个数,基本都需要离散化
离散化:先排序,再用\(unique\)函数去重,返回值是第一个重复的数,也就是\(end\),所以\(len=unique(a+1,a+n+1)-a-1\)。每次用\(lower_bound(b+1,b+len+1,a[i])-1\)获取\(a[i]\)的排名以离散化,函数是获得大于等于\(a[i]\)的第一个数的地址。注意最后输出值需要根据排名回溯。
#include<cstdio>
#include<algorithm>
#include<iostream>
#define ls p<<1
#define rs p<<1|1
#define re register
#define maxn 200010
using namespace std;
int a[maxn],b[maxn],cnt[maxn<<2];
int n,ans,len,tmp;
void push_up(int p){cnt[p]=cnt[ls]+cnt[rs];}
void insert(int p,int l,int r,int v)
{
if(l==r)
{
cnt[p]++;
return;
}
int mid=(l+r)>>1;
if(v<=mid) insert(ls,l,mid,v);
else insert(rs,mid+1,r,v);
push_up(p);
}
void query(int p,int l,int r,int qrank)
{
if(l==r)
{
ans=l;
return;
}
int mid=(l+r)>>1;
if(cnt[ls]>=qrank) query(ls,l,mid,qrank);
else query(rs,mid+1,r,qrank-cnt[ls]);
}
int main()
{
scanf("%d",&n);
for(re int i=1;i<=n;++i)
{
scanf("%d",a+i);
b[i]=a[i];
}
sort(b+1,b+n+1);
len=unique(b+1,b+n+1)-b-1;
for(re int i=1;i<=n;++i)
{
tmp=lower_bound(b+1,b+len+1,a[i])-b;
insert(1,1,len,tmp);
if(i%2)
{
ans=0;
query(1,1,len,(1+i)/2);
printf("%d\n",b[ans]);
}
}
return 0;
}
7.28
哈希\(hash\)
一维哈希、哈希冲突、无错哈希、二重哈希、哈希取子串
typedef unsigned long long ull;
ull base=131;
ull a[10010];
char s[10010];
int n,ans=1;
ull mod=998244353;
ull hashe(char s[])
{
int len=strlen(s);
ull ans=0;
for(int i=0;i<len;++i)
ans=(ans*base+(ull)s[i]);
return ans;
}
7.29
二维哈希:横向每行做一维哈希后再纵向将哈希数组哈希。
for(re int i=1;i<=n;++i)
for(re int j=1;j<=m;++j)//注意行列使用不同的base
a[i][j]=a[i][j-1]*base1+b[i][j];//这里要加b[i][j]
for(re int i=1;i<=n;++i)
for(re int j=1;j<=m;++j)
a[i][j]+=a[i-1][j]*base2;//这里不加
//对于(x1,y1)-(x2,y2)的矩阵
//fac[n]表示base的n次方
ans=a[x2][y2]-a[x2][y1-1]*fac1[y2-y1]-a[x1-1][y2]*fac2[x2-x1]+a[x1-1][y1-1]*fac1[y2-y1]*fac2[x2-x1];
\(base1=131,base2=1331\)
p2601 对称的正方形 二分答案+二维哈希
8.2
\(manacher\):\(O(n)\)求最长回文串与回文串个数
#include<cstdio>
#include<cstring>
#include<iostream>
#define maxn 30001000
using namespace std;
int n,hw[maxn],ans;
char a[maxn],s[maxn<<1];
void manacher()
{
int maxright=0,mid;
for(int i=1;i<n;++i)
{
if(i<maxright)
hw[i]=min(hw[(mid<<1)-i],hw[mid]+mid-i);
else hw[i]=1;
for(;s[i+hw[i]]==s[i-hw[i]];++hw[i])
if(hw[i]+i>maxright)
{
maxright=hw[i]+i;
mid=i;
}
}
}
void change()
{
s[0]=s[1]='#';
for(int i=0;i<n;++i)
{
s[i*2+2]=a[i];
s[i*2+3]='#';
}
n=n*2+2;
s[n]=0;
}
int main()
{
scanf("%s",a);
n=strlen(a);
change();
manacher();
ans=1;
for(int i=0;i<n;++i)
ans=max(ans,hw[i]);
/*for(int i=0;i<n;++i)
ans+=hw[i]/2;统计回文串数*/
printf("%d",ans-1);
}
8.3
\(manacher\)练习题:对称的正方形(见上文)
预处理后,用\(manahcer\)预先求出每个点为中心横向和纵向的回文串长度。例如设纵向延伸长度为\(lx[i][j]\)。
对于上下对称的图形,从中心向左延伸的距离一定小于等于这段区间上\(lx[i][j]\)的最小值,后者是\(RMQ\),可\(O(1)\)查询,最左端的点一定随中心点单调向右走,故总复杂度\(O(n^2)\)
如此上下左右都做一遍,对每个点取上下左右的最小值,再除去加上的点即可
8.4
\(RMQ\)问题:求区间最大值最小值--线段树、ST表
\(ST\)表:求静态\(RMQ\)问题,\(O(nlogn)\)预处理,\(O(1)\)查询
#include<cstdio>
#include<iostream>
#define maxn 200010
#define re register
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,m,f[maxn][23],lg[maxn],a[maxn],l,r,s;
int main()
{
n=read(),m=read();
for(re int i=1;i<=n;++i) a[i]=read(),f[i][0]=a[i];
for(re int i=2;i<=n;++i) lg[i]=lg[i>>1]+1;
for(re int j=1;j<=23;++j)
for(re int i=1;i+(1<<j)-1<=n;++i)
f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]);//类似LCA
for(re int i=1;i<=m;++i)
{
l=read(),r=read();
s=lg[r-l+1];
printf("%d\n",max(f[l][s],f[r-(1<<s)+1][s]));//s跟向下取整有关,这样取保证两个区间不会超出总区间,并保证两个区间并集覆盖总区间
}
return 0;
}
8.5
主席树(可持久化线段树):静态区间第\(k\)小
主席树学习笔记
#include<cstdio>
#include<iostream>
#include<algorithm>
#define re register
#define maxn 500010
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int a[maxn],rt[maxn],lc[maxn<<3],rc[maxn<<3],sums[maxn<<3];
int b[maxn],cnt,n,m,tmp,num,l,r,k,ans;
void build(int &t,int l,int r)
{
t=++cnt;
if(l==r) return;
int mid=(l+r)>>1;
build(lc[t],l,mid);
build(rc[t],mid+1,r);
}
int modify(int o,int l,int r)
{
int h=++cnt;
lc[h]=lc[o],rc[h]=rc[o],sums[h]=sums[o]+1;
if(l==r) return h;
int mid=(l+r)>>1;
if(tmp<=mid) lc[h]=modify(lc[h],l,mid);
else rc[h]=modify(rc[h],mid+1,r);
return h;
}
int query(int u,int v,int l,int r,int k)
{
int ans,mid=(l+r)>>1;
if(l==r) return l;
int x=sums[lc[v]]-sums[lc[u]];
if(x>=k) ans=query(lc[u],lc[v],l,mid,k);
else ans=query(rc[u],rc[v],mid+1,r,k-x);
return ans;
}
int main()
{
n=read(),m=read();
for(re int i=1;i<=n;++i) a[i]=read(),b[i]=a[i];
sort(b+1,b+n+1);
num=unique(b+1,b+n+1)-b-1;
build(rt[0],1,num);
for(re int i=1;i<=n;++i)
{
tmp=lower_bound(b+1,b+num+1,a[i])-b;
rt[i]=modify(rt[i-1],1,num);
}
for(re int i=1;i<=m;++i)
{
l=read(),r=read(),k=read();
ans=query(rt[l-1],rt[r],1,num,k);
printf("%d\n",b[ans]);
}
return 0;
}
8.8
树的数据生成器
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<ctime>
#include<algorithm>
#define maxn 2001000
#define re register
using namespace std;
int n,cnt2;
int cnt,x[10010],y[10010],z[10010],fa[10010],a[10010];
struct Edge{
int u,v,w;
}e[maxn];
int find(int x)
{
return fa[x]==x?x:(fa[x]=find(fa[x]));
}
int main()
{
srand(time(0));
n=rand()%10+1;
printf("%d\n",n);
for(re int i=1;i<=n;++i)
{
for(re int j=i+1;j<=n;++j)
{
x[++cnt]=i;
y[cnt]=j;
z[cnt]=rand()%100+1;
}
}
for(re int i=1;i<=cnt;++i) a[i]=i,fa[i]=i;
random_shuffle(a+1,a+cnt+1);
for(re int i=1;i<=cnt;++i)
{
int pos=a[i];
int eu=find(x[pos]),ev=find(y[pos]);
if(eu==ev) continue;
fa[ev]=eu;
e[++cnt2].u=x[pos],e[cnt2].v=y[pos],e[cnt2].w=z[pos];
if(cnt2==n-1) break;
}
for(re int i=1;i<=cnt2;++i)
{
printf("%d %d %d\n",e[i].u,e[i].v,e[i].w);
}
return 0;
}
8.10
\(KMP\)
#include<cstdio>
#include<iostream>
#include<cstring>
#define re register
#define maxn 1001000
using namespace std;
char A[maxn],B[maxn];
int p[maxn],lena,lenb;
void pre()
{
p[1]=0;
int j=0;
for(re int i=2;i<=lenb;++i)
{
while(B[i]!=B[j+1]&&j) j=p[j];
if(B[i]==B[j+1]) ++j;
p[i]=j;
}
}
void kmp()
{
int j=0;
for(re int i=1;i<=lena;++i)
{
while(A[i]!=B[j+1]&&j) j=p[j];
if(A[i]==B[j+1]) ++j;
if(j==lenb)
{
printf("%d\n",i-lenb+1);
j=p[j];
}
}
}
int main()
{
cin>>A+1>>B+1;
lena=strlen(A+1),lenb=strlen(B+1);
pre();
kmp();
for(re int i=1;i<=lenb;++i) printf("%d ",p[i]);
return 0;
}
8.12
字典树\(trie\)
将若干字符串形成树的结构,\(ch[u][c]\)表示\(u\)节点字符为\(c\)的后继
注意:1.需要将字符映射成数字,所以注意题目中字符的范围,专门写函数
2.若初始节点编号为1,则\(tot\)应初始化为1
3.注意细节,每循环一次结束,跳到下一个字符上,跳完再操作还是跳之前操作
4.有时\(for\)循环清零比\(memset\)清零快很多,尤其是有数据的范围已知时
5.可以很好存储字符串,比较好维护公共前缀,在上面可以搞一些\(kmp\)(AC自动机),\(dp,lca\)的操作,很多异或操作也可以用\(01trie\)维护
//题目:求一组字符串中是否有一个字符串是另一个字符串的前缀
#include<cstdio>
#include<iostream>
#include<cstring>
#define re register
#define maxn 100010
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int T,n,ch[maxn][26],tot;
char a[220];
bool flag,bo[maxn];
void insert(char *s)
{
int u=1,len=strlen(s);
for(int i=0;i<len;++i)
{
if(!ch[u][s[i]-'0']) ch[u][s[i]-'0']=++tot;
else if(i==len-1)//只要前面走了没有的分支就永远不会出现这个,出现这个代表这len位都匹配上了,当前字符串是前面字符串的前缀
flag=true;
u=ch[u][s[i]-'0'];
if(bo[u]) flag=true;//表示之前字符串是当前字符串的前缀,注意在跳一格之后再判断,因为第i(从1开始数)层循环结束后跳到字符的i位
}
bo[u]=true;//标记结尾
return;
}
int main()
{
T=read();
while(T--)
{
memset(ch,0,sizeof(ch));
memset(bo,0,sizeof(bo));
flag=false;
tot=1;//初始化为1!!!!因为第一个节点无信息
n=read();
for(re int i=1;i<=n;++i)
{
scanf("%s",a);//后面传指针,就别空一位读入了
insert(a);//把指针传进去,是从0位置开始的
}
if(!flag) printf("YES\n");
else printf("NO\n");
}
return 0;
}
8.17
\(AC\)自动机1
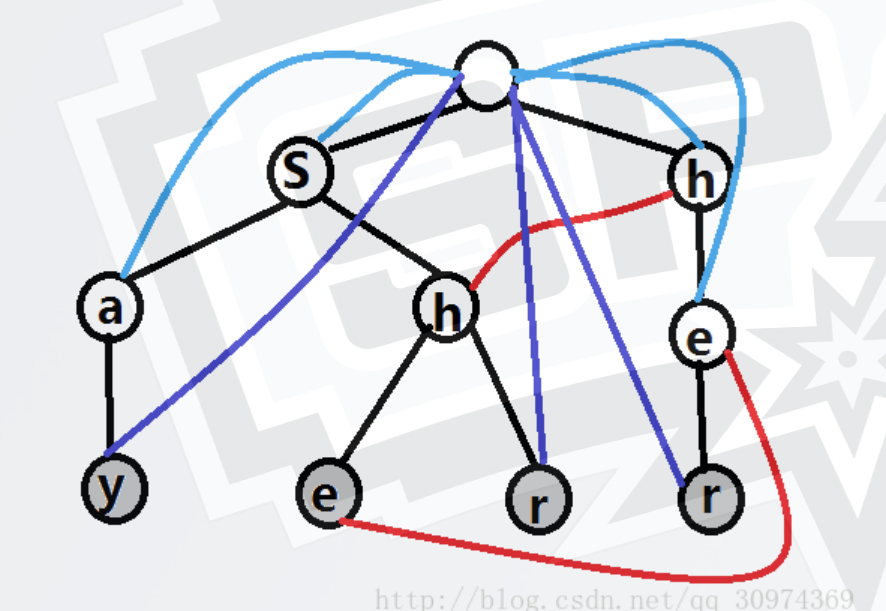
图片转自他人博客
题目:给出若干模式串和一个文本串,求有多少个模式串在文本串中出现
注意\(BFS\)字典图的构建有两种处理:
对于u节点,枚举26个字母,若他有v后继,则可求出\(fail[ch[u][v]]=ch[fail[u]][v]\),这样做是一种转移的过程,因为到\(fail[u]\)的串一定是到\(u\)的串的后缀,只需要看一下\(fail[u]\)有无后继v即可,若他本来没有,可以去寻找“代替者”,即第二种处理
第二种处理,其实也是失配处理,只不过不用fail数组记录,而是直接连边
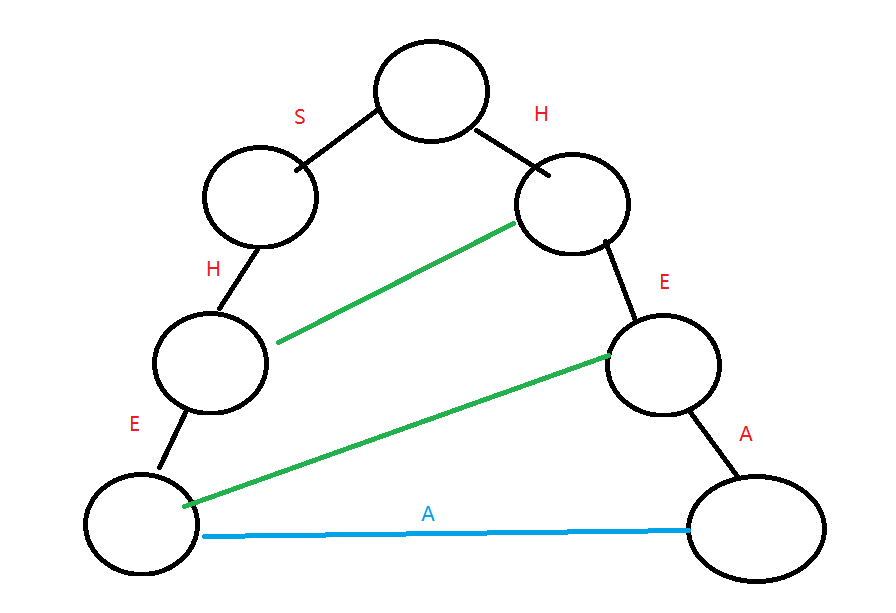
如图,绿色是正经的\(fail\)数组,,但如果我们在左侧最后找不到\(a\)这个后继,可以直接到\(e\)的失配指针处寻找有没有\(a\)的后继
而右侧的\(a\),也有可能是虚拟的,连向另外一条链
总之,以上两种方式都是在构建失配指针,构建字典图过程,是基于深度做失配指针的递归过程,递归边界是0节点
为什么要用两种方式?
想象在遍历模式串时,对于任意一个节点,都可以不停找他的\(fail\),看看是不是一个完整单词,因为这些节点以上的链一定也出现了,且这样做保证可以不遗漏
如果我们找不到一个节点,类似于\(KMP\)过程中失配了,那就直接走之前连好的边继续找
换句话说,第二种方式也可以像\(kmp\)那样写:我们如果找不到后继节点(当且仅当失配了),那就不断找\(fail\),看\(fail\)指向的节点有没有后继,如果有,那就从那里开始往后继续匹配,我们直接连边起始就是省略了跳的过程,一步到位!
#include<cstdio>
#include<cstring>
#include<iostream>
#include<queue>
#define maxn 1001000
#define re register
using namespace std;
int ch[maxn][26],bo[maxn],fail[maxn];
int n,tot;
char s[maxn];
void insert(char *s)
{
int u=0,len=strlen(s);
for(int i=0;i<len;++i)
{
int c=s[i]-'a';
if(!ch[u][c]) ch[u][c]=++tot;
u=ch[u][c];
}
bo[u]++;
}
queue<int> q;
void build()
{
for(re int i=0;i<26;++i)
if(ch[0][i]) q.push(ch[0][i]);
while(!q.empty())
{
int u=q.front();
q.pop();
for(re int i=0;i<26;++i)
{
if(ch[u][i]) //fail指针与直接连边
fail[ch[u][i]]=ch[fail[u]][i],q.push(ch[u][i]);
else
ch[u][i]=ch[fail[u]][i];
}
}
}
int AC(char *s)
{
int ans=0,u=0,len=strlen(s);
for(re int i=0;i<len;++i)
{
u=ch[u][s[i]-'a'];//实际上可能已经跳到别的链上了
for(re int j=u;j&&bo[j]!=-1;j=fail[j])
ans+=bo[j],bo[j]=-1;//把这些单词全部统计上,他们一定也符合要求
}
return ans;
}
int main()
{
scanf("%d",&n);
for(re int i=1;i<=n;++i)
{
scanf("%s",s);
insert(s);
}
build();
scanf("%s",s);
printf("%d\n",AC(s));
return 0;
}
8.19
\(AC\)自动机2:求出现最多的模式串及次数
#include<cstdio>
#include<iostream>
#include<cstring>
#include<string>
#include<algorithm>
#include<queue>
#define maxn 1001000
#define maxm 201000
#define re register
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int ch[maxm][26],bo[maxm],n,tot,ans,id[maxm],maxx,cnt[220];
int fail[maxm];
char s[220][220],t[maxn];
void insert(char *s,int k)
{
int u=0,len=strlen(s);
for(re int i=0;i<len;++i)
{
int c=s[i]-'a';
if(!ch[u][c]) ch[u][c]=++tot;
u=ch[u][c];
}
bo[u]++;
if(!id[u]) id[u]=k;//题目要求按顺序输出,可能有重复模式串,所以输出最靠前一个,只用记录最靠前的编号即可
}
queue<int> q;
void build()
{
for(re int i=0;i<26;++i)
if(ch[0][i]) q.push(ch[0][i]);
while(!q.empty())
{
int u=q.front();
q.pop();
for(re int i=0;i<26;++i)
{
if(ch[u][i])
fail[ch[u][i]]=ch[fail[u]][i],q.push(ch[u][i]);
else
ch[u][i]=ch[fail[u]][i];
}
}
}
void AC(char *s)
{
int u=0,len=strlen(s);
for(re int i=0;i<len;++i)
{
u=ch[u][s[i]-'a'];
for(int j=u;j;j=fail[j])
{
cnt[id[j]]+=bo[j];//不写+1也是为了应对出现重复模式串的情况
maxx=max(maxx,cnt[id[j]]);//对应编号计数
//注意这里bo[j]会用多次,不要标记
}
}
}
int main()
{
while(1)
{
n=read();
if(n==0) break;
memset(bo,0,sizeof(bo));
memset(ch,0,sizeof(ch));
memset(id,0,sizeof(id));//记录trie树上节点对应字符串的编号
memset(cnt,0,sizeof(cnt));//记录出现次数
memset(fail,0,sizeof(fail));
tot=ans=maxx=0;
for(re int i=1;i<=n;++i)
{
scanf("%s",s[i]);
insert(s[i],i);
}
build();
scanf("%s",t);
AC(t);
printf("%d\n",maxx);
for(re int i=1;i<=n;++i) if(cnt[i]==maxx) printf("%s\n",s[i]);
}
return 0;
}
8.26
扫描线
统计网格图矩形面积并,坐标为格点坐标
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define re register
#define maxn 400100
#define ls p<<1
#define rs p<<1|1
#define ll long long
using namespace std;
inline int read()
{
int x=0,f=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
};
ll tmp,ans;
int n,x_,y_,x__,y__,cnt1,cnt2,sums[maxn<<2],val[maxn],len,tmp1,tmp2,lenn[maxn<<2],cnt[maxn<<2];
struct node{
int x,yu,yd,k;
}e[maxn<<2];
bool cmp(node A,node B)
{
return A.x<B.x;
}
void push_up(int p,int l,int r)
{
if(cnt[p]) lenn[p]=val[r+1]-val[l];//这里仔细琢磨,cnt在线段树中是不上传的,也就意味着如果cnt[p]>0那这一段一定全被线段覆盖,如果cnt[p]<0,也一定被上方线段全覆盖,否则cnt[p]=0,没有被线段
//完全覆盖,从下方上传即可
else lenn[p]=lenn[ls]+lenn[rs];
}
void update(int p,int l,int r,int ql,int qr,int k)
{
if(ql<=l&&r<=qr)
{
cnt[p]+=k;
push_up(p,l,r);//注意最底下也需要上传一下
return;
}
int mid=(l+r)>>1;
if(ql<=mid) update(ls,l,mid,ql,qr,k);
if(qr>mid) update(rs,mid+1,r,ql,qr,k);
push_up(p,l,r);
}
int main()
{
n=read();
for(re int i=1;i<=n;++i)
{
x_=read(),y_=read(),x__=read(),y__=read();
e[++cnt1].x=x_,e[cnt1].yu=y__,e[cnt1].yd=y_,e[cnt1].k=1;
e[++cnt1].x=x__,e[cnt1].yu=y__,e[cnt1].yd=y_,e[cnt1].k=-1;//一个矩形上下边都存下来
val[++cnt2]=y_,val[++cnt2]=y__;
}
sort(val+1,val+cnt2+1);
len=unique(val+1,val+cnt2+1)-val-1;//离散化纵坐标,使之成为一个个区间
for(re int i=1;i<=(n<<1);++i)
{
tmp1=lower_bound(val+1,val+len+1,e[i].yu)-val;
tmp2=lower_bound(val+1,val+len+1,e[i].yd)-val;
e[i].yu=tmp1,e[i].yd=tmp2;
}
sort(e+1,e+cnt1+1,cmp);
for(re int i=1;i<(n<<1);++i)
{
update(1,1,len-1,e[i].yd,e[i].yu-1,e[i].k);//排序后就是从下往上扫,每次扫到新的停下更新下答案
ans+=(ll)lenn[1]*(e[i+1].x-e[i].x);
}
printf("%lld\n",ans);
return 0;
}

